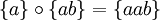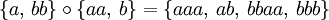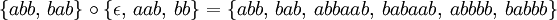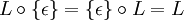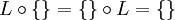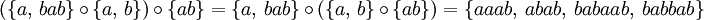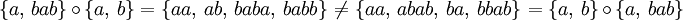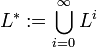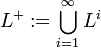- Wortmenge
-
Eine formale Sprache ist eine Menge von Wörtern, welche aus einem gegebenen Alphabet gebildet werden können (einschließlich des leeren Wortes). Sie ist definiert als eine Teilmenge der Kleeneschen Hülle über dem gegebenen Alphabet. Eine Teilmenge der formalen Sprachen kann mit Hilfe einer formalen Grammatik beschrieben werden, welche die Wörter der Sprache herzuleiten gestattet.Die Theorie der formalen Sprachen ist eine Teildisziplin der Mathematik und stellt ein eigenständiges Wissensgebiet in der theoretischen Informatik dar.
Die Menge der Wörter einer formalen Sprache kann endlich oder unendlich sein, wobei dann auch der Begriff einer endlichen bzw. unendlichen (formalen) Sprache verwendet wird. Wenn die Menge der Wörter der formalen Sprache gleich der leeren Menge ist, spricht man auch von der leeren Sprache. Man beachte hier, dass die Sprache, welche nur das leere Wort enthält, selbst nicht leer, sondern einelementig ist.
Die formale Grammatik einer bestimmten formalen Sprache erlaubt gelegentlich zu entscheiden, ob ein bestimmtes vorgegebenes Wort zu dieser formalen Sprache gehört oder nicht. In anderen Fällen ist das nicht so. Bei formalen Sprachen mit einem unendlichen Wortvorrat ist vielfach die Entscheidung über die Zugehörigkeit nicht möglich, obwohl man theoretisch alle Wörter einer formalen Sprache über die Grammatik erzeugen kann. [1]
Inhaltsverzeichnis
Formale Sprachen, die natürliche Sprachen beschreiben
Wenn wir die Wörter einer natürlichen Sprache als Alphabetszeichen ansehen, dann bilden die Sätze der natürlichen Sprache eine formale Sprache über dem Alphabet der natürlichsprachlichen Wörter. Allerdings entziehen sich natürliche Sprachen meist einer vollständigen Definition, die schließlich festlegt, welche Sätze zu der natürlichen Sprache gehören und welche nicht. Grundsätzlich können Gesetze und Mechanismen der formalen Sprachen daher bislang nur auf Teilbereiche der natürlichen Sprachen angewendet werden. Siehe dazu Linguistik.
Auch ein anderer Aspekt natürlicher Sprachen, ihre dynamische Erweiterbarkeit, wird von der Theorie der formalen Sprachen nicht erfasst. Ein weiteres Fremdwort, Lehnwort oder eine Wortneuschöpfung und beinahe jedes neu entdeckte Wortspiel würden immer einer komplett neuen, anderen formalen Sprache bedürfen, um sie adäquat und vollständig mathematisch oder informatisch darstellen zu können.
Um eine natürliche Sprache in etwa mithilfe formaler Sprachen zu beschreiben, benötigt man in der Regel eine ganze Anzahl eigener formaler Sprachen. Auf die geschriebene deutsche Sprache angewandt, ist leicht zu erkennen, dass es wenigstens drei eigenständige formale Sprachen sein werden, um aus dem lateinischen Alphabet sinnvolle deutsche Texte herzuleiten; die erste erzeugt die Wörter aus den Buchstaben (Wortbildungsregeln), die zweite arrangiert Wörter zu grammatisch korrekten Sätzen (Syntaxregeln), die dritte selektiert sinnvolle Sätze aus den grammatisch korrekten und gruppiert diese zu sinnvollen Texten (Semantikregeln).
Beispiele
- Die Programmiersprache C ist eine formale Sprache. Die Wörter von C sind die jeweiligen Programme. Das Alphabet von C sind die Schlüsselwörter und Zeichen, die in der Definition von C festgelegt sind.
- Die natürlichen Zahlen in unärer Darstellung:
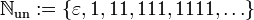
- Die unäre Sprache, die nur Wörter quadratischer Länge enthält:
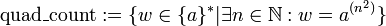
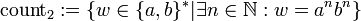
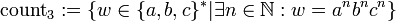
- Die Sprache aller Palindrome:
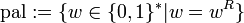
wobei wR die Spiegelung des Wortes w ist. - Die Dezimalkodierung der Primzahlen:
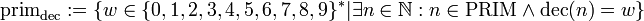 .
.
Hierbei bezeichnet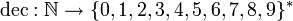 die Kodierung der natürlichen Zahlen im Dezimalsystem und PRIM steht für die Menge der Primzahlen.
die Kodierung der natürlichen Zahlen im Dezimalsystem und PRIM steht für die Menge der Primzahlen. - Die Morse- oder Thue-Folge:
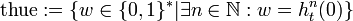 .
.
Wobei ht ein Homomorphismus ist, der folgendermaßen definiert ist: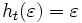 und ht(w0): = ht(w)01, ht(w1): = ht(w)10.
und ht(w0): = ht(w)01, ht(w1): = ht(w)10.
Somit sind die ersten Elemente der Thue-Folge: 0, 01, 0110, 01101001, 0110100110010110, ...
Operationen auf formalen Sprachen
Da eine Sprache eine Menge von Wörtern ist, können alle Operationen, die auf Mengen anwendbar sind, wie die Vereinigung, Durchschnitt und die Differenz zweier Mengen bzw. das absolute Komplement einer Menge auch auf Sprachen angewandt werden. Dabei ist das Universum des absoluten Komplements einer Sprache L die Kleenesche Hülle des Alphabets, über dem L definiert wurde. Zusätzlich sind folgende Operationen definiert:
Konkatenation
Die Konkatenation zweier Sprachen L1 und L2 ist die Sprache der Wörter, welche sich aus der Konkatenation (Verkettung) aller Wörter der ersten mit allen Wörtern der zweiten Sprache ergeben:
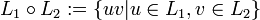 .
.
So sind zum Beispiel die Konkatenationen von verschiedenen Sprachen über dem Alphabet
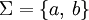 :
:Das neutrale Element der Konkatenation ist die Sprache, welche nur das leere Wort enthält. So gilt für jede beliebige Sprache L:
Das Nullelement der Konkatenation ist die leere Sprache, so dass für jede Sprache
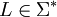 gilt:
gilt:Die Konkatenation von Sprachen ist wie die Konkatenation von Wörtern assoziativ, aber nicht kommutativ. So ist zum Beispiel:
aber:
Da außerdem die Potenzmenge der Kleeneschen Hülle eines beliebigen Alphabets Σ (die gleich der Menge aller Sprachen ist, die aus Σ gebildet werden können) abgeschlossen bezüglich Konkatenation ist, bildet sie zusammen mit der Konkatenation als Operator und der Sprache des leeren Wortes als neutrales Element einen Monoiden.
Potenz
Die Potenz Ln einer Sprache ist die n-fache Konkatenation dieser Sprache mit sich selbst. Sie ist rekursiv definiert mit:
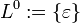
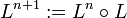 (für
(für 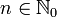 )
)
So sind zum Beispiel:
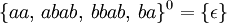
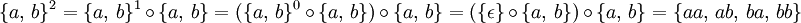
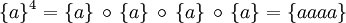
- {}0 = {ε}
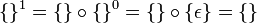
Im Speziellen gilt für jede einelementige, formale Sprache L = {w} (mit
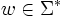 ) und jedes
) und jedes 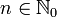 :
:- Ln = {w}n = {wn}
Kleene-*-Abschluss und Kleene-+-Abschluss
Der Kleene-*-Abschluss L * (auch Iteration genannt) und der Kleene-+-Abschluss L + einer formalen Sprache L sind definiert über die Vereinigung der Potenzsprachen von L:
Siehe auch: Kleenesche Hülle
Wichtige formale Sprachklassen
- Noam Chomsky hat eine Hierarchie von formalen Grammatiken aufgestellt, die verschiedene Typen von formalen Sprachen erzeugen. Diese ist heute unter dem Namen Chomsky-Hierarchie bekannt. Hier wird unterschieden zwischen Typ 0, Typ 1, Typ 2 und Typ 3: Rekursiv aufzählbare, kontextsensitive, kontextfreie bzw. reguläre Sprachen.
- Aristid Lindenmayer hat ein Regelsystem vorgeschlagen, in dem Ersetzungsschritte in jedem Schritt an jeder Stelle parallel durchgeführt werden. Diese Systeme heißen L-Systeme.
- Mit Semi-Thue-Systemen lassen sich Sprachen festlegen, die aus Startwörtern abgeleitet werden.
- Mit Church-Rosser-Systemen werden Sprachen erklärt, deren Wörter sich auf ein Terminalwort reduzieren lassen.
- Termersetzungssysteme erzeugen die Menge von Termen, die zu einem Ausgangsterm äquivalent sind.
- Verallgemeinerungen von formalen Sprachen erhalten wir mit Graphgrammatiken, mit denen wir Graphsprachen erzeugen können.
- Hypergraphgrammatiken erzeugen Hypergraphen, eine Verallgemeinerung von Graphen.
Hinweise und Quellen
- ↑ Das ergibt sich aus der Nichtentscheidbarkeit des allgemeinen Halteproblems für Turingmaschinen, denn man kann jeder formalen Sprache eine bestimmte, individuelle Turingmaschine eindeutig zuordnen und umgekehrt.
Siehe auch
Anwendungen siehe in:
- Berechenbarkeitstheorie
- Komplexitätstheorie
- Kryptographie
- Kryptoanalyse
- Compilerbau
- Programmiersprache
Literatur
- Lars Peter Georgie: Berechenbarkeit, Komplexität, Logik. Vieweg, Braunschweig Wiesbaden,
- Eine dritte Auflage erschien 1995.
- Englische Ausgabe: Computability, Complexity, Logic. Erschienen in der Reihe: Studies in logic and the foundations of mathematics. North Holland, Amsterdam 1985.
-
- Eine Darstellung der Formalen Sprachen im Kontext der Berechenbarkeitstheorie, Logik und Komplexitätstheorie. Stellt hohe Anforderungen an den Leser, liefert dafür tiefe Einblicke.
- Michael A. Harrison: Introduction to Formal Language Theory. Erschienen in der Reihe: Series in Computer Science, Addison-Wesley, 1978.
-
- Eine sehr ausführliche und viel gelobte Einführung.
- John E. Hopcroft and Jeffrey D. Ullman: Einführung in die Automatentheorie, Formale Sprachen und Komplexitätstheorie. Addison-Wesley, 1988.
- Englisches Original: Introduction to Automata Theory, Languages and Computation. Addison-Wesley, 1979.
- Eine überarbeitete dritte Auflage auf deutsch erschien 1994 bei der Oldenbourg R. Verlag GmbH. Im Jahr 2004 erschien bei Addison-Wesley eine zweite überarbeitete Auflage.
-
- Das englische Original ist das in der Theoretischen Informatik am häufigsten zitierte Buch. Die Beweise sind in älteren deutschen Übersetzungen gelegentlich falsch wiedergegeben. Dieses Buch ist in zahlreiche Sprachen übersetzt worden.
- Grzegorz Rozenberg und Arto Salomaa: The Mathematical Theory of L-Systems. Academic Press, New York, 1980.
-
- Das ausführlichste Buch über L-Systeme.
- Grzegorz Rozenberg und Arto Salomaa (Herausgeber): Handbook of Formal Languages. Volume I-III, Springer, 1997, ISBN 3-540-61486-9.
-
- Eine ausführliche Übersicht über die wichtigsten Gebiete der Formalen Sprachen dargestellt jeweils von aktiv in diesem Gebiet arbeitenden Wissenschaftlern.
- Arto Salomaa: Formale Sprachen. Springer, 1978.
- Englisches Original: Formal Languages. Academic Press, 1973.
- Ingo Wegener: Theoretische Informatik. Teubner Stuttgart, 1993. ISBN 3-519-02123-4.
-
- In der Darstellung der Formalen Sprachen wird stets die Komplexität der formal-sprachlichen Konstruktionen mitbehandelt. Diese ist sonst nur in der Originalliteratur zu finden.
- U. Hedtstück: Einführung in die Theoretische Informatik - Formale Sprachen und Automatentheorie. Oldenbourg Verlag, München 2000, ISBN 3-486-25515-0
- S. Abramsky, Dov M. Gabbay, T.S.E. Maibaum (eds.): Handbook of logic in computer science. Vol. 5: Logical and algebraic methods. Oxford University Press 2000, ISBN 0-19-853781-6
- Mogens Nielsen, Wolfgang Thomas: Computer Science Logic. Springer 1998, ISBN 3540645705
Wikimedia Foundation.