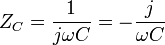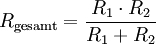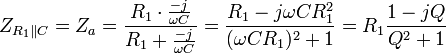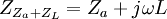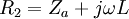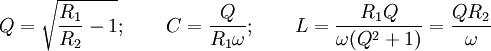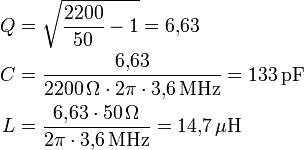Boucherot-Schaltung

Ein Resonanztransformator, auch Boucherot-Schaltung, ist eine schwingkreisähnliche Schaltung aus Kondensator und Spule, um auf einer vorgegebenen Frequenz Leistungsanpassung zwischen Bauelementen oder Baugruppen zu erreichen. Bei Hochfrequenzanwendungen entfällt im Regelfall der Eisenkern der Spule, bei niederfrequenten Anwendungen können bei Spule auch Ferritkerne zur Anwendung kommen.

Spule L und Kondensator C bilden einen Resonanztrafo

Trotz der ähnlichen Bezeichnung hat die Schaltung des Resonanztransformators nichts unmittelbar mit einem Transformator zur Spannungs- bzw. Stromtransformation zu tun.

Allgemeines

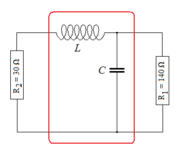
Zur Bestimmung der Werte der Spule L und Kondensator C zwecks Leistungsanpassung müssen auf beiden Seiten die Impedanzen des Resonanztransformators den Beträgen der beiden externen Widerstände R₁ bzw. R₂ entsprechen.

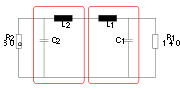
Leistungsanpassung bedeutet, dass in obiger Schaltung, mit beispielhaften Widerstandwerten für R₁ und R₂, entweder

• eine Quelle (links) mit dem Innenwiderstand R₂ = 30 Ω möglichst viel Leistung an den Verbraucher R₁ = 140 Ω abgeben soll oder
• eine Quelle (rechts) mit dem Innenwiderstand R₁ = 140 Ω möglichst viel Leistung an den Verbraucher R₂ = 30 Ω abgeben soll.

In beiden Fällen erscheint der Wert des Verbrauchers um einen gewissen Faktor vergrößert oder verringert hinsichtlich des Wertes auf der anderen Seite des in der Abbildung rot eingerahmten Resonanztransformators.

Die Dimensionierung des Resonanztransformators kann entweder graphisch mit einem Smith-Diagramm oder wie im folgenden rechnerisch im Rahmen der komplexen Wechselstromrechnung erfolgen. Dabei gelten die Kirchhoffschen Regeln, und die Gesetze für Reihenschaltung und Parallelschaltung. Der induktive Widerstand Z_L der Spule L mit der Kreisfrequenz ω = 2·π·f ist gegeben durch

Z_L = jωL

und für den kapazitiven Widerstand Z_C des Kondensators C

$Z_C = \frac{1}{j \omega C} = - \frac{j}{\omega C}$

Berechnung

Für den Ersatzwiderstand R_gesamt zweier parallel geschalteter Widerstände gilt allgemein

$R_\mathrm{gesamt} = \frac{R_1 \cdot R_2}{R_1 + R_2}$

Wendet man diese Formel auf die Parallelschaltung von R₁ und C an und ersetzt R₂ durch die Impedanz des Kondensators, ergibt sich

$Z_{R_1\|C} = Z_a = \frac{R_1 \cdot \frac{-j}{\omega C}}{R_1 + \frac{-j}{\omega C}} =\frac{R_1-j\omega CR_1^2}{(\omega CR_1)^2+1} =R_1\frac{1-jQ}{Q^2+1}$

mit der Hilfsgröße Q = R₁ωC, dem Gütefaktor. Für den Ersatzwiderstand einer Reihenschaltung muss man die Einzelwiderstände addieren; in diesem Fall ergibt sich

$Z_{Z_a + Z_L}=Z_a+j\omega L$

Für Leistungsanpassung gilt bei dieser (oben gezeigten) Schaltung

$\,R_2=Z_a+j\omega L$

Diese komplexe Gleichung zerfällt bei bekannten Werten von ω, R₁ und R₂ in zwei reelle Bestimmungsgleichungen für L und C, da der Imaginärteil der rechten Gleichungsseite Null sein muss. Die Lösungen lauten:

$Q=\sqrt{\frac{R_1}{R_2}-1}; \qquad C=\frac{Q}{R_1\omega}; \qquad L=\frac{R_1 Q}{\omega (Q^2+1)}=\frac{QR_2}{\omega}$

Beispiel: Die Leistungsanpassung im Bild soll für die Frequenz 100 MHz berechnet werden. Damit ist Q = 1,915; C = 22 pF und L = 91 nH.

Beispiel: Anpassung einer Dipolantenne

Dipol mit Anpassschaltung für Koaxkabel

Der Eingangswiderstand einer Dipolantenne hängt stark vom Ort der Einspeisung ab. Trennt man die Dipolmitte auf und schließt dort ein Symmetrisches Kabel an, muss man dessen Impedanz auf etwa 74 Ω auslegen, um Leistungsanpassung zu erreichen. Ist das Dipol (wie im nebenstehenden Bild) in der Mitte nicht unterbrochen, kann man die Leistung unsymmetrisch an einem Ende einspeisen. Bei dünnen Drahtantennen misst man an dieser Stelle eine Impedanz von etwa 2200 Ω. Im Regelfall ist die Funkstation mit der Antenne über ein unsymmetrisches Koaxkabel der Impedanz 75 Ω oder 50 Ω verbunden, deshalb muss ein verlustarmer Transformator dazwischengeschaltet werden, um eine krasse Fehlanpassung zu vermeiden. Da eine Dipolantenne nur eine relativ geringe Bandbreite von wenigen Prozent der Mittenfrequenz besitzt, ist ein schmalbandiger Resonanztrafo sehr gut zur Widerstandsanpassung geeignet.

Für eine Frequenz von 3,6 MHz und ein 50 Ω-Kabel ergeben sich folgende Werte:

$\begin{align} Q &= \sqrt{\frac{2200}{50}-1}=6{,}63\\ C &= \frac{6{,}63}{2200\,\Omega \cdot 2\pi\cdot 3{,}6\, \mathrm{MHz}}=133\,\mathrm{pF}\\ L &= \frac{6{,}63\cdot 50\,\Omega}{2\pi\cdot 3{,}6\, \mathrm{MHz}}=14{,}7\,\mu\mathrm H \end{align}$

Diese Schaltung hat gegenüber der sonst gebräuchlichen Einspeisung am „Strombauch“ in der Dipolmitte einige Vorteile:

• Die Resonanzfrequenz der Antenne kann durch geringe Abweichung von C oder L um etwa 10 % von den berechneten Werten verschoben werden, ohne dass das Stehwellenverhältnis unzulässig große Werte annimmt. Das entspricht einer vergrößerten Bandbreite der Antenne.
• Der Resonanztrafo ist gut erreichbar am Ende der Antenne montiert.
• Bei langen Drahtantennen hängt in der Dipolmitte kein schweres Koaxkabel mit Balun.

Pi-Filter

Pi-Filter zur Widerstandstransformation

In der Hochfrequenztechnik betreibt man vorzugsweise Leistungstransistoren und Elektronenröhren als Schalter (C-Betrieb), um durch hohen Wirkungsgrad unnötige Verlustwärme zu vermeiden. Gemäß den Gesetzen der Fourieranalyse entstehen durch abruptes Ein- und Ausschalten einer Spannung viele Oberwellen, die abgestrahlt werden und die Funktion anderer Geräte stören. Um das zu verhindern, müssen Tiefpassfilter oder Schwingkreise oder Resonanztransformatoren ausreichend hoher Güte Q eingebaut werden. Aus Erfahrung weiß man, dass ab Q ≥ 8 die Oberwellen der Wechselspannung gut unterdrückt werden.

Bei den eben beschriebenen, einfachen Resonanztransformatoren hängt Q ausschließlich vom Verhältnis der Widerstände an Ein- und Ausgang ab. Wenn die Widerstände etwa gleichen Wert haben, ist Q zu gering, um nennenswerte Filterwirkung sicherzustellen. Das lässt sich durch Kombination zweier Resonanztransformatoren ändern. Die Schaltung erinnert an den griechischen Buchstaben π, deshalb setzte sich die Bezeichnung Pi-Filter durch. Mitunter wird auch die Bezeichnung „Collinsfilter“ verwendet, weil sie durch ihre guten Eigenschaften in Funkgeräten dieser Firma bekannt wurde.

Die Berechnung der Bauelemente erfolgt in zwei Stufen: Der Widerstand R₂ wird durch C₂ und L₂ auf einen sehr geringen Zwischenwert R₃ ≈ 1 Ω herabtransformiert, den man sich an der Verbindung der beiden roten Rechtecke denken kann. R₃ ist aber nicht als Bauelement vorhanden, sondern dieser fiktive Zwischenwert wird durch C₁ und L₁ auf den gewünschten Widerstand R₁ hochtransformiert. Da beide Resonanztransformatoren hohe Gütefaktoren Q aufweisen, wird die erwünschte Filterwirkung erreicht. Mit einer geringen Änderung der berechneten Werte muss gerechnet werden, wenn L₁ und L₂ zu einer einzigen Spule vereint werden.

Anwendungen

Resonanztrafo zur Energieversorgung einer Leuchtröhre

Anwendungen findet der Resonanztransformator in unterschiedlichen Bereichen. Im folgenden sind einige Anwendungsbereiche beispielhaft aufgezählt.

• In Funkgeräten und der Hochfrequenztechnik verwendet man aus Resonanztransformatoren gebildete Bandfilter, die einen eng begrenzten Frequenzbereich von einer Verstärkerstufe zur nächsten übertragen. Dies umfasst beispielsweise:
  • bestimmte Symmetrierglied-Arten zur Anpassung der Wellenimpedanz eines Kabels mittels an eine Antenne (Impedanztransformation).
  • Anpassung zwischen zwei aufeinanderfolgenden Verstärkerstufen (Transistoren).

• Zur Übertragung elektrischer Leistung in Form spezieller Schaltnetzteile, den Resonanzwandlern, zur Umsetzung zwischen verschiedenen Spannungsniveaus:
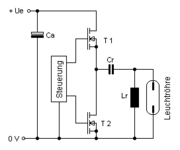
  • Zum Betrieb von Kaltkathodenröhren bei Flachbildschirmen oder in elektronischen Vorschaltgeräten für Kompaktleuchtstofflampen und Energiesparlampen zur Erzeugung der notwendigen Betriebsspannung der Röhren. Typisch ist, dass diese Wandler bei noch nicht gezündeter Kaltkathodenröhre aufgrund der dann hohen Ausgangsimpedanz selbsttätig die erforderliche hohe Zündspannung bereitstellen. Dabei wird bei Betrieb an Kleinspannung und zur galvanischen Trennung der Resonanztransformator mit einem echten Transformator gebildet^[1].
  • In Fernsehempfängern mit Kathodenstrahlröhre arbeitet der zur Speisung der Zeilenablenkspulen notwendige Zeilentransformator beim Zeilenrücklauf als Resonanzwandler und erzeugt dann die Anodenspannung der Bildröhre.
  • Bei quasiresonanten Schaltnetzteilen finden die Schaltübergänge als resonante Halbschwingung statt; damit lassen sich die Schaltverluste drastisch senken.
  • Der Tesla-Transformator erzeugt durch Resonanz Spannungen weit über 100 kV.

Einzelnachweise

1. ↑ Resonanzwandler von Jörg Rehrmann: Das Netzteil- und Konverterhandbuch