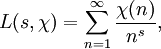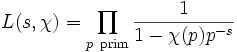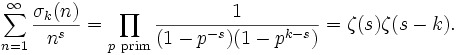- Euler-Produkt
-
Dirichletreihen sind Reihen, die in der analytischen Zahlentheorie verwendet werden, um zahlentheoretische Funktionen mit Methoden aus der Analysis, insbesondere der Funktionentheorie zu untersuchen. Viele offene zahlentheoretische Fragestellungen sind durch diesen Zusammenhang einer „Näherungslösung“ (durch Abschätzungen) zugänglich geworden, etwa Fragen nach der Verteilung von Primzahlen.
Konvergente Dirichletreihen sind als analytische Funktionen auch losgelöst von zahlentheoretischen Problemen als Untersuchungsgegenstand interessant, da sie in engem Zusammenhang mit Potenzreihen stehen, und eine ähnlich „natürliche“ Darstellung von analytischen Funktionen erlauben.
Ihren Namen tragen diese Reihen zu Ehren des Mathematikers Peter Gustav Lejeune Dirichlet.
Inhaltsverzeichnis
Definition und formale Eigenschaften
Eine Dirichletreihe ist eine Reihe der Form
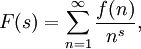 mit
mit 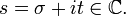
Für gewisse Koeffizientenfolgen f(n) und komplexe Zahlen s konvergiert diese Reihe absolut. Das Produkt von zwei absolut konvergenten Dirichletreihen ist nun wieder eine absolut konvergente Dirichletreihe und die Koeffizienten ergeben sich durch Faltung der Koeffizientenfolgen als zahlentheoretische Funktionen. Damit entspricht die Multiplikation von absolut konvergenten Dirichletreihen der Faltung ihrer Koeffizienten.
Gelegentlich findet man in der Literatur (etwa bei Zagier) auch die allgemeinere Definition
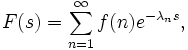 mit
mit 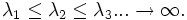
Mit
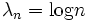 ergibt dies wieder die erste Definition, mit λn = n erhält man
ergibt dies wieder die erste Definition, mit λn = n erhält man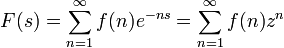 mit z = e − s,
mit z = e − s,
also eine gewöhnliche Potenzreihe.
Der Raum der formalen Dirichletreihen wird mit einer Multiplikation versehen, indem man die für absolut konvergente Reihen gültige Multiplikationsregel auf beliebige (auch nichtkonvergente) Dirichletreihen überträgt. (Zu dieser Konstruktion vergleiche auch die analoge Begriffsbildung formale Potenzreihe.) Dadurch wird der Raum der formalen Dirichletreihen mit der punktweisen Addition, der Skalarmultiplikation und der Faltung isomorph (als Ring und Algebra) zu den zahlentheoretischen Funktionen und erbt alle Strukureigenschaften dieses Raumes.Der Isomorphismus ordnet jeder zahlentheoretischen Funktion f(n) die formale Dirchletreihe zu, deren Koeffizientenfolge sie ist. Diese Dirichletreihe F(s) heißt dann die von f(n) erzeugte Dirichletreihe.
Konvergente Dirichletreihen
Zu jeder Dirichletreihe, die irgendwo aber nicht überall konvergiert, existiert eine reelle Zahl σ0, so dass die Reihe in der Halbebene Re(z)>σ0 konvergiert und in der Halbebene Re(z)<σ0 divergiert. Über das Verhalten auf der Geraden Re(z) =σ0 lässt sich keine allgemeine Aussage machen. Falls die Dirichletreihe überall bzw. nirgends konvergiert, so setzt man
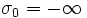 bzw.
bzw. 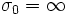 und nennt in allen Fällen
und nennt in allen Fällen ![\sigma_0\in [-\infty,\infty]](/pictures/dewiki/101/e659de1ead764706cc203a3a5fd17e73.png) die Konvergenzabszisse der Dirichletreihe.
die Konvergenzabszisse der Dirichletreihe.Ähnlich, wie man im Falle von Potenzreihen den Konvergenzradius berechnen kann, kann man auch im Falle von Dirichletreihen die Konvergenzabszisse mit einem Limes superior aus ihrer Koeffizientenfolge bestimmen, es gilt:
Ist
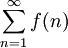 divergent, so ist
divergent, so ist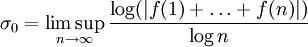 .
.
Ist hingegen
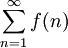 konvergent, so ist
konvergent, so ist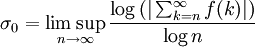 .
.
Analytische Eigenschaften
In ihrer Konvergenzhalbebene Re(z)>σ0 ist die Dirichletreihe kompakt konvergent und stellt dort eine holomorphe Funktion F(s) dar.
Die Ableitungen der so bestimmten holomorphen Funktion F können durch gliedweise Differentiation gewonnen werden. Ihre kte Ableitung ist die Dirichletreihe
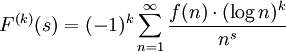 .
.
Eulerprodukte
Dirichletreihen mit multiplikativen zahlentheoretischen Funktionen als Koeffizienten lassen sich als Eulerprodukt darstellen. Ist f(n) eine multiplikative zahlentheoretische Funktion und konvergiert die von ihr erzeugte Dirichletreihe F(s) für die komplexe Zahl s absolut, dann gilt
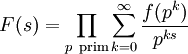 .
.
Im Falle einer vollständig multiplikativen Funktion vereinfacht sich dieses Produkt zu
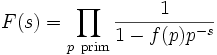 .
.
Diese unendlichen Produkte über alle Primzahlen heißen Eulerprodukte. Der Wert dieser Produkte ist definiert als Grenzwert
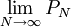 der Folge endlicher Produkte PN, die entsteht, indem man das Produkt nur auf Primzahlen unterhalb einer Schranke N erstreckt.
der Folge endlicher Produkte PN, die entsteht, indem man das Produkt nur auf Primzahlen unterhalb einer Schranke N erstreckt.Wichtige Dirichletreihen
Riemannsche Zetafunktion
Die berühmteste Dirichletreihe ist die Riemannsche Zetafunktion
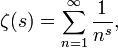 .
.
Sie wird von der zahlentheoretischen 1-Funktion I0(n) (mit I0(n) = 1 fur alle n) erzeugt. Da diese Funktion vollständig multiplikativ ist, hat die Zeta-Funktion die Eulerproduktdarstellung
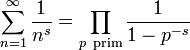
Dirichletreihe der Teilerfunktion
Die Teilerfunktion ist das „Faltungsquadrat“ der 1-Funktion.
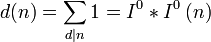 ,
,
die ihr zugeordnete Dirchletreihe ist also das Quadrat der Zetafunktion:
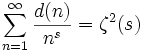 .
.
Dirichletreihe der Möbiusfunktion
Die Möbiusfunktion μ(n) ist multiplikativ mit μ(pk) = 0 für k > 1. Also hat die von ihr erzeugte Dirichletreihe M(s) das Eulerprodukt
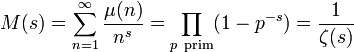 .
.
Die Relation M(s)·ζ(s)=1 überträgt sich auf die zugehörigen zahlenthoretischen Funktionen und bedeutet dort:
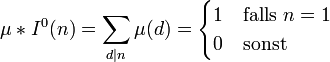 .
.
Dirichletsche L-Reihen
Die ebenfalls von Dirichlet eingeführten L-Reihen
werden von einem Dirichlet-Charakter χ erzeugt. Diese Reihen spielen eine wichtige Rolle beim Beweis des Dirichletschen Satzes über die Existenz unendlich vieler Primzahlen in arithmetischen Progressionen. Da Dirichletcharaktere vollständig multiplikativ sind, kann man die L-Reihen als Eulerprodukte darstellen
und für χ = χ1, den Hauptcharakter modulo k gilt:
Dirichletreihe der Λ-Funktion
Die von Mangoldtsche Funktion Λ(n) spielt eine Rolle beim Beweis des Primzahlsatzes. Diese zahlentheoretische Funktion ist definiert als
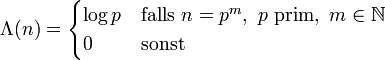 ,
,
die von ihr erzeugte Dirichletreihe lässt sich durch die Zeta-Funktion ausdrücken:
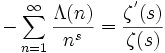 .
.
Dirichletreihe der Eulerschen φ-Funktion
Die Eulersche φ-Funktion ist multiplikativ mit
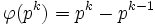 für
für 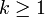 .
.
Das Eulerprodukt der von ihr erzeugten Dirichletreihe ist
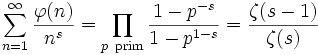 .
.
Dirichletreihe der verallgemeinerten Teilerfunktion
Die verallgemeinerte Teilerfunktion σk(n) ist multiplikativ und für Primzahlpotenzen ist
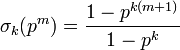 .
.
Daher hat die Dirichletreihe von σk die Eulerproduktdarstellung:
Siehe auch
Weblinks
- Planetmath (englisch) zum Stichwort Dirichlet series
- Mathworld (englisch) zum Stichwort Dirichlet series
Literatur
- Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory. Springer Verlag New York u. a. 1990, ISBN 0-387-97127-0
- Jörg Brüdern: Einführung in die analytische Zahlentheorie. Springer Verlag, Berlin u. a. 1995, ISBN 3-540-58821-3
- Graham James Oscar Jameson: The Prime Number Theorem. Cambridge University Press, Cambridge u. a. 2004, ISBN 0-521-89110-8
- Konrad Knopp: Theorie und Anwendung der unendlichen Reihen. 2. Auflage. In: Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete. Springer Verlag , Berlin u. a. 1996, ISBN 3-540-59111-7
- Max Koecher, Aloys Krieg: Elliptische Funktionen und Modulformen, 2. Aufl., Springer, Berlin (2007) ISBN 978-3-540-49324-2
- Don Zagier: Zetafunktionen und quadratische Körper. Springer Verlag Berlin u. a. 1981, ISBN 3-540-10603-0
Wikimedia Foundation.