2-Körper Problem

Unter Zweikörperproblem, unter astronomischen Gesichtspunkten Keplerproblem, versteht man die Aufgabe, die Bahnbewegung eines einzelnen Körpers (Himmelskörpers) um ein Schwerezentrum genau zu berechnen, wenn sich nur diese zwei Körper durch Newtonsche Gravitation (d.h. im 1/r Gravitationspotential und instantaner Fernwirkung) gegenseitig beeinflussen.

Ursprünglich wurde angenommen, das Zweikörperproblem würde zur Beschreibung eines heliozentrischen Kosmos ausreichen. Tatsächlich hat sich aber gezeigt, dass das Keplerproblem eine Idealisierung darstellt, die so in der Natur nicht zu finden ist. Ungeachtet dessen ist die Lösung der Frage die Grundlage moderner Himmelsmechanik.

Die Keplersche Lösung

Der Großteil der Lösung geht auf Johannes Kepler zurück:

• 1. und 2. Keplersches Gesetz (gefunden 1599 bis 1609, der Ellipsen- und der Flächensatz) und
• 3. Keplersches Gesetz (1619, in der Weltharmonie veröffentlicht).
• die Keplergleichung

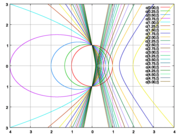
Als mögliche Bahnen (Keplerbahnen) kommen Kreise, Ellipsen, Parabeln und Hyperbeln in Frage. Bei Kreisen und Ellipsen sind die Körper aneinander gebunden wie die Planeten an die Sonne. Ist die Bahnform parabolisch oder hyperbolisch, so findet nur eine Begegnung statt.

Mögliche Bahnkurven nach Kepler

Die nebenstehende Zeichnung stellt die verschiedenen Bahnkurven für ein Zweikörperproblem dar. Die verschieden Bahnkurven werden durch eine positive reelle Zahl, die sogenannte numerische Exzentrizität charakterisiert. Gebundene Bahnen (Kreise und Ellipsen) haben eine numerische Exzentrizität von ε < 1, wobei der Kreis einer Exzentrizität ε = 0 entspricht. Größere Exzentrizitäten führen zu offenen Bahnen (Parabeln mit ε = 1 und Hyperbeln mit ε > 1).

Die exakte Differentialgleichung lautet: $\ddot{\vec r} = - \gamma M \frac{\vec r}{\left| \vec r \right|^3}$

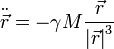
Anwendung in der Himmelsmechanik

Mit den drei Keplerschen Gesetzen und jeweils sechs Bahnelementen lässt sich die Position jedes Himmelskörpers berechnen, wenn außer ihm und der Sonne keine weiteren Körper wirksam sind.
Tatsächlich bewirken die anderen Körper des Sonnensystems so genannte Bahnstörungen, welche die auf zwei Körpern beruhenden, elliptischen Kepler-Bahnen zu leicht spiraliger Form verzerren.

Zur kompletten Lösung des Zweikörperproblems sind auch Methoden notwendig, um die sechs Bahnelemente eines im Sonnensystem umlaufenden Körpers bestimmen zu können. Sie gehen auf Sir Isaac Newton und Pierre-Simon Laplace bzw. Carl Friedrich Gauß zurück (Bahnbestimmung).

Im Zweikörperproblem (ohne Bahnstörungen durch dritte Körper und nicht-gravitative Einflüsse) genügen diese sechs Bahnelemente. Eine elegante Methode zu ihrer Bestimmung ist die Ausnutzung zweier zeitlich konstanter Vektoren (entspricht wegen je drei Komponenten sechs Erhaltungsgrößen): des Drehimpulses und des Laplace-Runge-Lenz-Vektors.

Grenzen der Zwei-Körper-Lösung

Zum Dreikörperproblem wird die Aufgabe der Bahnberechnung, wenn die Gravitation eines dritten Körpers (wegen seiner Größe meist Jupiter) berücksichtigt werden soll. Es ist jedoch nicht streng lösbar – außer für die Spezialfälle der fünf Lagrange-Punkte.

Die Keplerlösung ist aber die Basis aller modernen Planetentheorien (wie auch Mondtheorien und den Bewegungstheorien aller anderen Himmelskörper), die auf der idealisierten Lösung Keplers weitere Terme aufbringen und so zu komplexen Kalkülen herangewachsen sind. Ihre Grenzen finden sie weniger in der Genauigkeit, sondern der Oskulation, der zeitlichen Begrenztheit.

Resumé:

• Zweikörperproblem direkt gelöst durch Keplers drei Gesetze und himmelsmechanische Methoden zur Berechnung der sechs Bahnelemente – siehe auch Doppelsterne.
• Dreikörperproblem nur iterativ lösbar, Bahnstörungen bewirken kleine Änderungen in den sechs Bahnelementen.
• Allgemeine Mehrkörper-Probleme löst man als Mechanische Simulation.

Anmerkung: Im Rahmen der allgemeinen Relativitätstheorie besitzt das Zweikörperproblem wegen der Abstrahlung von Gravitationswellen und dem damit verbundenen Drehimpulsverlust keine stabile Lösung. Vielmehr werden die Orbits um den Schwerpunkt immer enger, bei kürzer werdender Umlaufzeit.

Literatur

• Andreas Guthmann: Einführung in die Himmelsmechanik und Ephemeridenrechnung. BI-Wiss.-Verl., Mannheim 1994, ISBN 3-411-17051-4.