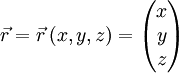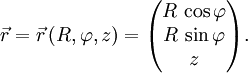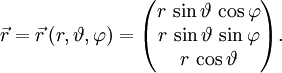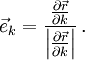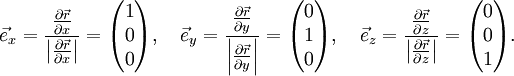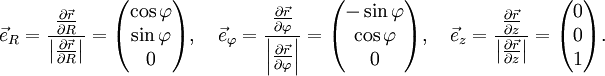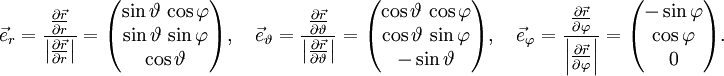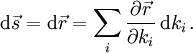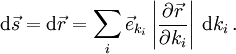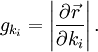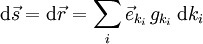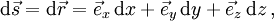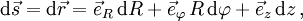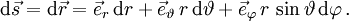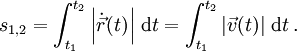- Radiusvektor
-
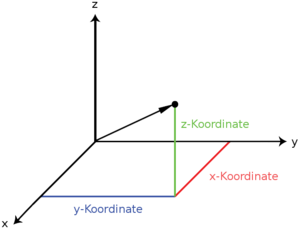
Als Ortsvektor bezeichnet man in der Mathematik und Physik einen Vektor, der von einem festen Bezugspunkt zu einem bestimmten Punkt, dem Aufpunkt, zeigt. Der Ortsvektor wird auch als Aufpunktvektor oder Radiusvektor bezeichnet. Der Vorteil eines Ortsvektors besteht darin, dass mit seiner Hilfe die Position des Aufpunktes ohne Festlegung auf ein bestimmtes Koordinatensystem dargestellt werden kann.
Inhaltsverzeichnis
Ortsvektor in verschiedenen Koordinatensystemen
Der durch einen Ortsvektor beschriebene Aufpunkt kann durch die Koordinaten eines Koordinatensystems beschrieben werden, wobei der Bezugspunkt des Ortsvektors normalerweise in den Koordinatenursprung gelegt wird.
Kartesische Koordinaten
Üblicherweise wird der Ortsvektor in kartesischen Koordinaten in der Form
definiert. Daher sind die kartesischen Koordinaten gleichzeitig die Komponenten des Ortsvektors.
Zylinderkoordinaten
Der Ortsvektor als Funktion von Zylinderkoordinaten ergibt sich durch Umrechnen der Zylinderkoordinaten in die entsprechenden kartesischen Koordinaten zu
Kugelkoordinaten
Der Ortsvektor als Funktion von Kugelkoordinaten ergibt sich durch Umrechnen der Kugelkoordinaten in die entsprechenden kartesischen Koordinaten zu
Basisvektoren
Die Basisvektoren in den verschiedenen Koordinatensystemen ergeben sich durch Normierung der partiellen Ableitungen des Ortsvektors nach den jeweiligen Koordinaten. Allgemein ergibt sich der zur Koordinate k gehörende Basisvektor zu
Kartesische Koordinaten
Die Basisvektoren
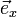 ,
, 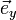 und
und 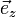 sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.
sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.Zylinderkoordinaten
Die Basisvektoren
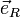 ,
, 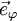 und
und 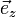 sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.
sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.Kugelkoordinaten
Die Basisvektoren
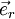 ,
, 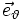 und
und 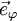 sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.
sind zueinander orthonormal und bilden in dieser Reihenfolge ein Rechtssystem.Wegelement
Ein Wegelement oder Linienelement
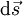 kann als totales Differential
kann als totales Differential 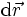 des Ortsvektors dargestellt werden. Allgemein ergibt sich für das vektorielle Wegelement bei Verwendung der Koordinaten
des Ortsvektors dargestellt werden. Allgemein ergibt sich für das vektorielle Wegelement bei Verwendung der Koordinaten 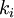 :
:Mit der obenstehenden Gleichung für die Basisvektoren kann man auch schreiben
Die Beträge der Ableitungen des Ortsvektors
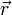 nach den Koordinaten
nach den Koordinaten 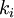 heißen metrische Koeffizienten
heißen metrische KoeffizientenDamit kann man das vektorielle Wegelement in der Form
darstellen. Für die bisher betrachteten Koordinatensysteme ergeben sich daraus die folgenden Darstellungsformen:
- Kartesische Koordinaten:
- Zylinderkoordinaten:
- Kugelkoordinaten:
Relativistische Koordinaten
In der speziellen Relativitätstheorie (SRT) werden Raum und Zeit als eine zusammenhängende, vierdimensionale pseudoriemannsche Mannigfaltigkeit, der sogenannten Raumzeit, beschrieben. Ein Punkt auf dieser Mannigfaltigkeit, der durch 3 Raumkoordinaten und eine Zeitkoordinate festgelegt wird, wird als Ereignis bezeichnet. Für jeweils zwei Ereignisse kann durch die Minkowski-Metrik ein Linienelement ds definiert werden, welches zur Eigenzeit proportional ist.
- ds2 = ημνdxμdxν = c2dt2 − dx2 − dy2 − dz2.
Hierbei bezeichnet ημν = diag(1, − 1, − 1, − 1) die Minkowski-Metrik und dxμ das Vierervektordifferential.
Physik
In der Physik sind viele Größen vom Ortsvektor abhängig, wie etwa die Geschwindigkeit und Beschleunigung eines Massenpunktes, oder eine Dichteverteilung.
Der Betrag des Ortsvektors ist die Entfernung des Punktes vom Ursprung, da der Betrag gerade die Länge des Vektors ist.
Die Ableitung des Ortsvektors
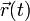 nach der Zeit t ergibt den Geschwindigkeitsvektor
nach der Zeit t ergibt den Geschwindigkeitsvektor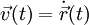 .
.
Durch nochmalige Ableitung ergibt sich der Beschleunigungsvektor
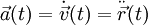 .
.
Trajektorie
Als Trajektorie bezeichnet man den Weg, auf dem sich ein Punkt (z. B. der Schwerpunkt eines Körpers) bewegt. Wenn man die Position eines Punktes durch einen Ortsvektor
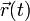 beschreibt, der von einem Parameter t (z. B. der Zeit) abhängt, so beschreibt die Abbildung
beschreibt, der von einem Parameter t (z. B. der Zeit) abhängt, so beschreibt die Abbildung 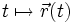 bei Variation von t eine Trajektorie, d. h. zu jedem Wert von t gibt es einen bestimmten Punkt im Raum. Die Menge aller Punkte des Weges heißt Kurve, hier speziell Bahnkurve.
bei Variation von t eine Trajektorie, d. h. zu jedem Wert von t gibt es einen bestimmten Punkt im Raum. Die Menge aller Punkte des Weges heißt Kurve, hier speziell Bahnkurve.Wenn beispielsweise
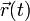 die zeitabhängige Bewegung eines Punktes beschreibt, so ergibt sich für die Länge des zwischen den Zeitpunkten t1 und t2 zurückgelegten Weges:
die zeitabhängige Bewegung eines Punktes beschreibt, so ergibt sich für die Länge des zwischen den Zeitpunkten t1 und t2 zurückgelegten Weges:Himmelsmechanik
In der Himmelsmechanik wird der Orts- oder Radiusvektor verwendet, um die Position eines Himmelskörpers bezogen auf das Schwerezentrum anzugeben, um welches er sich auf einer Umlaufbahn bewegt (Gravizentrisches Koordinatensystem). Der Radiusvektor liegt hierbei stets in Richtung der Gravitationslinie und die Strecke des Ortsvektors wird Fahrstrahl genannt. Der Fahrstrahl ist die zentrale Größe des zweiten Keplergesetzes (Flächensatz).
Siehe auch: Hodograph
Siehe auch
Literatur
- Alexander Heigl: Mathematische Einführung in die Elektrizitätslehre (PDF, 649 kB). Lehrstuhl für Technische Elektrophysik, Technische Universität München. 18. Oktober 2006.
- Klaus Desch: Mathematische Ergaenzungen zur Physik II, Kapitel 11: Vektoranalysis (PDF, 210 kB). Institut für Experimentalphysik, Hamburg.
Wikimedia Foundation.