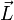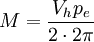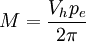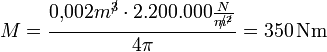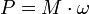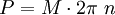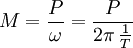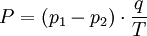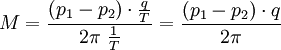- Bremsmoment
-
Physikalische Größe Name Drehmoment Größenart Moment Formelzeichen der Größe M Größen- und
Einheiten-
systemEinheit Dimension SI Nm M L2 T −2 Als Drehmoment bezeichnet man jene physikalische Größe, die bei der Beeinflussung der Drehzahl (Zunahme oder Abnahme) eines drehbaren Körpers wirkt.
Das Drehmoment wird in Newtonmeter (Einheitenzeichen: Nm) gemessen und ist das Vektorprodukt von Kraftarm und Kraft.
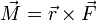 – Drehmomentvektor
– Drehmomentvektor- Drehmoment ist Kraftarm mal Kraft.
Das Drehmoment ist ein Spezialfall eines Moments, der für rotierende Körper und Systeme benutzt wird. Es spielt dabei eine vergleichbare Rolle wie die Kraft bei der geradlinigen Schiebebewegung (Translationsbewegung). Siehe hierzu auch die Tabelle in Rotation (Physik). Ein Antriebsmoment kann einen Drehkörper (z. B. ein Rad) um seine Drehachse rotatorisch beschleunigen, sodass die Drehzahl des Rades steigt. Ein in die andere Richtung gerichtetes Bremsmoment kann die Drehzahl des Rades reduzieren. Sind Antriebs- und Bremsmoment gleich groß (Momentengleichgewicht), dann ändert der Drehkörper seine Drehzahl nicht.
Die physikalische Dimension des Drehmomentes ist damit das Produkt aus Kraft und Weg. Im SI-System hat es die (abgeleitete) Maßeinheit Newton-Meter,
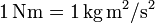 .
.Inhaltsverzeichnis
Grundlagen
Wirkt auf den Schwerpunkt eines frei beweglichen starren Körpers eine Kraft, so wird der Körper beschleunigt, das heißt, seine Geschwindigkeit verändert sich. Er führt eine geradlinige Translationsbewegung (Verschiebung) aus. Wird der Körper jedoch an einem Punkt festgehalten, so ist keine Translation mehr möglich, und die Bewegungsmöglichkeit des Körpers reduziert sich auf Rotationsbewegungen (Drehungen) um diesen Punkt. Die Größe, die diese Drehbewegung beeinflusst, d. h. die Änderung der Rotationsgeschwindigkeit verursacht, heißt Drehmoment.
Eine einzelne Kraft
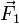 kann keine reine Drehbewegung verursachen. Eine Veränderung der Drehbewegung ohne Änderung der Translationsbewegung ist erst möglich, wenn ein Kräftepaar angreift. Die zweite Kraft wird beispielsweise durch die drehbare Befestigung des Körpers aufgebracht. Ist die zweite Kraft entgegengesetzt gleich der ersten Kraft,
kann keine reine Drehbewegung verursachen. Eine Veränderung der Drehbewegung ohne Änderung der Translationsbewegung ist erst möglich, wenn ein Kräftepaar angreift. Die zweite Kraft wird beispielsweise durch die drehbare Befestigung des Körpers aufgebracht. Ist die zweite Kraft entgegengesetzt gleich der ersten Kraft, 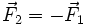 , so ist die resultierende Kraft auf den Körper null, und die Translationsbewegung ändert sich nicht. Trotzdem bewirkt dieses Kräftepaar ein Drehmoment auf den Körper und dadurch eine Veränderung der Drehbewegung. Dabei ist neben der Größe der beiden Kräfte
, so ist die resultierende Kraft auf den Körper null, und die Translationsbewegung ändert sich nicht. Trotzdem bewirkt dieses Kräftepaar ein Drehmoment auf den Körper und dadurch eine Veränderung der Drehbewegung. Dabei ist neben der Größe der beiden Kräfte 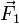 und
und 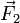 auch der Abstand der beiden Punkte, an denen die Kräfte angreifen, von Bedeutung. Der Abstand
auch der Abstand der beiden Punkte, an denen die Kräfte angreifen, von Bedeutung. Der Abstand 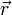 ist ein Vektor, der vom Angriffspunkt der Kraft
ist ein Vektor, der vom Angriffspunkt der Kraft 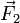 zum Angriffspunkt von
zum Angriffspunkt von 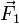 zeigt. Zum Drehmoment trägt nur die Komponente
zeigt. Zum Drehmoment trägt nur die Komponente 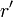 von
von 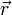 bei, die senkrecht auf der Richtung der Kraft
bei, die senkrecht auf der Richtung der Kraft 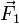 (oder
(oder 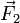 ) steht.
) steht. 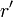 ist der Abstand, in dem die beiden Kräfte wirken.
ist der Abstand, in dem die beiden Kräfte wirken.- Der Betrag des Drehmomentes ist dann das Produkt von
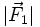 mit r'
mit r'
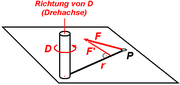
- Die Richtung des Drehmomentes ist senkrecht zur durch die Kraft
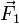 und den Abstandsvektor
und den Abstandsvektor 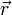 aufgespannten Ebene gelegen, in derjenigen Richtung, in die der Daumen zeigt, wenn man mit den gekrümmten Fingern der rechten Hand in Richtung der durch das Drehmoment hervorgerufenen Drehbewegung zeigt. Diese „Rechte-Hand-Regel“ ist eine (willkürliche) Festlegung, die durchgängig bei allen Berechnungen der technischen Mechanik verwendet wird.
aufgespannten Ebene gelegen, in derjenigen Richtung, in die der Daumen zeigt, wenn man mit den gekrümmten Fingern der rechten Hand in Richtung der durch das Drehmoment hervorgerufenen Drehbewegung zeigt. Diese „Rechte-Hand-Regel“ ist eine (willkürliche) Festlegung, die durchgängig bei allen Berechnungen der technischen Mechanik verwendet wird.
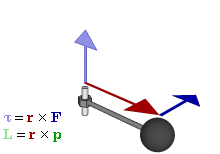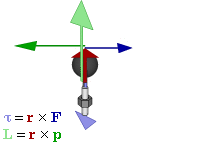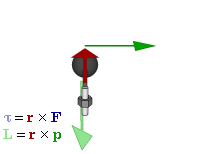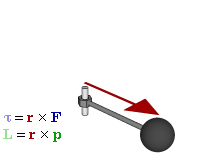
Dieser Zusammenhang zwischen den auf den Körper wirkenden Kräften, dem Abstandsvektor der beiden Angriffspunkte und dem Drehmoment (in Betrag und Richtung) wird in kompakter Form durch das Kreuzprodukt (Vektorprodukt) ausgedrückt. In dieser Darstellung erhält man für das Drehmoment
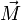 die Definition:
die Definition: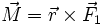 .
.
- Hauptartikel: D'Alembertsches Prinzip
Wirkt auf einen Körper eine, von null verschiedene, resultierende Kraft, z. B., weil nur eine einzige Kraft
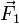 von außen einwirkt, so wird der Körper nach dem 2. Newtonschen Gesetz beschleunigt. Nach dem d'Alembertschen Prinzip wird dies im beschleunigten Bezugssystem so beschrieben, dass eine Trägheitskraft (Scheinkraft)
von außen einwirkt, so wird der Körper nach dem 2. Newtonschen Gesetz beschleunigt. Nach dem d'Alembertschen Prinzip wird dies im beschleunigten Bezugssystem so beschrieben, dass eine Trägheitskraft (Scheinkraft) 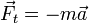 berücksichtigt wird. Wenn die Wirklinie der Kraft
berücksichtigt wird. Wenn die Wirklinie der Kraft 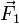 nicht durch den Schwerpunkt geht, dann bilden
nicht durch den Schwerpunkt geht, dann bilden 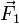 und
und 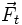 ein Kräftepaar, das ein Drehmoment erzeugt (obwohl im beschleunigten Bezugssystem die Summe aller Kräfte einschließlich der Trägheitskraft null ergibt!).
ein Kräftepaar, das ein Drehmoment erzeugt (obwohl im beschleunigten Bezugssystem die Summe aller Kräfte einschließlich der Trägheitskraft null ergibt!).Die Beschreibung des gleichen Vorgangs im ruhenden System (Inertialsystem) kommt ohne Trägheitskräfte aus. Hier bewirkt
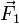 sowohl eine Beschleunigung als auch ein Drehmoment
sowohl eine Beschleunigung als auch ein Drehmoment 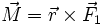 und damit eine Winkelbeschleunigung (Beispiel: Anschneiden eines Balles durch seitliches Treten etc.).
und damit eine Winkelbeschleunigung (Beispiel: Anschneiden eines Balles durch seitliches Treten etc.).Messung des Drehmoments
Drehmomentmesseinrichtungen
- Drehmomentmesswelle
- Pendelmaschine
- Pronyscher Zaum
- Wasserwirbelbremse
Unterschiedliches Auftreten des Drehmomentes
In der Technik ist es gebräuchlich, dem Drehmoment unterschiedliche Bezeichnungen zu geben, je nachdem in welchem Zusammenhang sie wirken:
Man unterscheidet je nach der Richtung, in der Leistung fließt, zweierlei Drehmomente:
- Antriebsmoment ist das Drehmoment, womit die Maschine etwas antreibt und Leistung abgibt.
- Abtriebsmoment ist das Drehmoment, womit die Maschine angetrieben wird und Leistung aufnimmt.
- Antriebsmoment eines Motors (für Verbrennungsmotor siehe Link unten)
- Abtriebsmoment eines Generators, eines Kompressors oder einer Pumpe
- Antriebsmoment und Abtriebsmoment eines Getriebes
- Anfahrmoment einer Gasturbine
- Anzugsmoment einer Schraube
- Drehmoment in der Propellerwelle eines Schiffes oder eines Motorflugzeugs.
Beispiel: Elektromotor
Der Asynchronmotor in der Ausführung als Kurzschlussläufer ist der am häufigsten verwendete Elektromotor. Das Bild zeigt das erzeugte Drehmoment in Abhängigkeit von der Drehzahl. Der normale Betriebsbereich ist rechts von den Kipppunkten K1 oder K2 auf der steil abfallenden Kurve. Der Bereich links von den Kipppunkten ist der Anlaufbereich, der immer möglichst schnell durchfahren werden muss. Im Anlaufbereich hat der E-Motor ein schlechten Wirkungsgrad und kann ohne Schutzmaßnahmen durchbrennen.
Beispiel: Drehmoment eines Verbrennungsmotors
Der bei Automobilen verwendete Begriff maximales Drehmoment eines Verbrennungsmotors bei einer bestimmten Drehzahl bezeichnet das maximale vom Motor an der Kurbelwelle abgegebene Drehmoment. Das an der Kurbelwelle bei Volllast (Vollgas) abgegebene Drehmoment ist nicht über den gesamten Drehzahlbereich des Motors konstant, sondern hat in einem bestimmten Bereich des nutzbaren Drehzahlbereiches ein Maximum.
Das Drehmoment M für Viertaktmotoren berechnet sich aus:
Hierbei ist Vh das Hubvolumen und pe der effektive Mitteldruck, der Faktor 2π im Nenner stammt aus der Formel für die Arbeit eines Drehmoments, die entlang des Umfanges 2π verrichtet wird. Der Wert 2π wird bei Viertaktmotoren mit 2 multipliziert, da Viertaktmotoren nur bei jeder zweiten Umdrehung Arbeit verrichten. Für Zweitaktmotoren gilt entsprechend:
Rechenbeispiel für das Drehmoment eines Serienfahrzeuges mit 2000 cm³ (=0,002 m³) Hubvolumen, dessen Viertaktmotor bei einer Drehzahl von 2000 1/min einen Mitteldruck von 22 Bar (=2.200.000 Pa; 1 Pa = 1 N/m²) erreicht, in SI-Einheiten gerechnet:
Beispiel: Zusammenhang von Drehmoment und Leistung
Die Leistung bei einer Drehbewegung ergibt sich zu
Die Winkelgeschwindigkeit ω erhält man aus der Drehzahl n gemäß
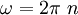 . Damit ergibt sich für die Leistung
. Damit ergibt sich für die Leistungund für eine drehzahlabhängige Leistung
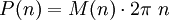
- M(n) ist die für die untersuchte Maschine typische drehzahlabhängige Drehmomentkenngröße, die durch Messung erhalten wird.
Ein Verbrennungsmotor, der bei 2000 Umdrehungen pro Minute ein Drehmoment von 350 Nm abgibt, gibt somit bei dieser Drehzahl auch eine Leistung von
 ab.
ab.
Beispiel: Drehmoment eines Hydraulikmotors
Für die Leistung P gilt:
Damit ergibt sich für das Drehmoment
mit der Periodendauer T, welche einer Umdrehung des Motors entspricht.
Die hydraulische Leistung P errechnet sich aus Druck p1 und p2 am Motoreingang bzw. Ausgang und q des geschluckten Ölvolumens pro Umdrehung (Periode T)
Die Formel der hydraulischen Leistung eingesetzt in obige Formel ergibt das Drehmoment
Siehe auch
Weblinks
Wikimedia Foundation.

 ,
,  ,
,  ,
,