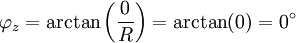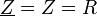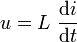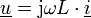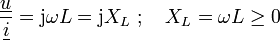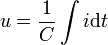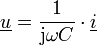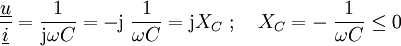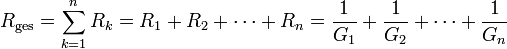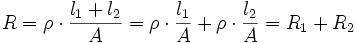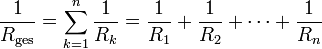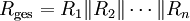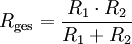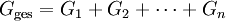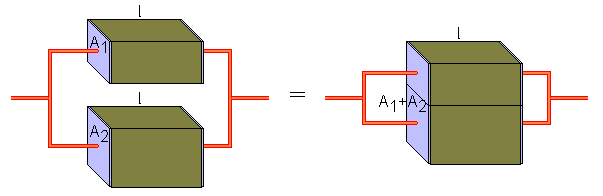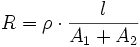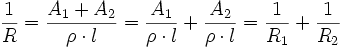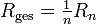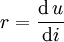- Differenzieller Widerstand
-
Physikalische Größe Name Elektrischer Widerstand Formelzeichen der Größe R, Z, X Größen- und
Einheiten-
systemEinheit Dimension SI Ohm (Ω) M·L2/(I2·T3) Der elektrische Widerstand ist in der Elektrotechnik ein Maß dafür, welche elektrische Spannung erforderlich ist, um einen bestimmten elektrischen Strom durch einen elektrischen Leiter fließen zu lassen. Als Formelzeichen für den elektrischen Widerstand wird in der Regel R – wahrscheinlich abgeleitet vom Lateinischen resistere für „widerstehen“ (evtl. auch von den französischen oder englischen Entsprechungen, genaue Herkunft unbekannt) verwendet. Der Widerstand hat die SI-Einheit Ohm, sein Einheitenzeichen ist das große Omega (Ω).
Verwandt mit dem Widerstand ist der spezifische elektrische Widerstand (Formelzeichen ρ). Bei diesem Wert handelt es sich um eine temperaturabhängige Materialkonstante, die eine von der geometrischen Form des ausgeführten Leiters unabhängige Beschreibung der Widerstandseigenschaft ermöglicht.
Inhaltsverzeichnis
Geschichte
Die elektrische Ladung war seit Coulomb bekannt, die elektrische Spannung seit Volta und die Wirkung des elektrischen Stromes seit Ampère. Georg Simon Ohm kannte die Kraftwirkung der elektrischen Spannung, deshalb konnte er Spannungen durch Kraftmessungen bestimmen. Die Stärke von Strömen konnte er anhand chemischer Prozesse quantitativ bestimmen. Man wusste, dass elektrische Ströme etwas mit der Bewegung der coulombschen Ladungen zu tun haben. Die gesetzmäßigen Zusammenhänge zwischen Spannung und Stromstärke waren unbekannt.
Erste Versuche ließen keine klaren Gesetzmäßigkeiten erkennen. Erst als Ohm [1] begann, einen langen und sehr dünnen stromdurchflossenen Draht auf möglichst konstanter Temperatur zu halten, erkannte er die Proportionalität zwischen Spannung U und Stromstärke I :
Diese Proportionalität zwischen Spannung und Stromstärke wird durch das von ihm formulierte und nach ihm benannte ohmsche Gesetz beschrieben:
Der von U und I unabhängige Proportionalitätsfaktor R ist der elektrische Widerstand. Dieses einfach erscheinende Gesetz wurde zu einer Zeit gefunden, als es noch keine „richtigen“ Spannungsquellen gab, geschweige denn Spannungs- oder Strommesser. Zudem waren die Messungen von anderen physikalischen Effekten überlagert. Auch waren die Begriffe Spannung, Stromstärke und Widerstand noch nicht allgemein etabliert. Erst vor diesem Hintergrund kann man seine wissenschaftliche Leistung würdigen.
Ohm war aber in Deutschland kein angesehener Wissenschaftler, Professuren wurden ihm zunächst verweigert. Das änderte sich erst, als ihm zahlreiche Würdigungen aus dem Ausland zuteil wurden.
Ohmscher Widerstand
Ein ohmscher Widerstand ist ein elektrischer Widerstand, dessen Widerstandswert im Idealfall unabhängig von der Spannung, der Stromstärke und der Frequenz ist. An einem solchen ohmschen Widerstand gilt das ohmsche Gesetz für beliebige Spannungen, Ströme und Frequenzen. Wenn man die Stromstärke I über der Spannung U in Form eines U-I-Diagramms aufträgt, erhält man eine Ursprungsgerade, der Zusammenhang also ist direkt proportional :
Näherungsweise und mit Einschränkungen kann ein ohmscher Widerstand durch ein Bauelement, im einfachsten Fall einen Metalldraht, realisiert werden, das üblicherweise ebenfalls einfach Widerstand – siehe Widerstand (Bauelement) − genannt wird.
Wenn Strom durch einen Widerstand fließt und Spannung daran abfällt, wird elektrische Leistung gemäß
in Wärmeleistung umgesetzt.
Der ohmsche Widerstand wird auch als Gleichstromwiderstand bezeichnet. Sein Kehrwert, also der Proportionalitätsfaktor zwischen Stromstärke und Spannung, heißt elektrischer Leitwert G des Leiters. Es gilt also:
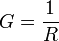 .
.
Berechnung des Widerstands eines Leiters
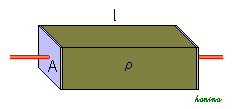
Der ohmsche Widerstand eines Körpers lässt sich aus seinen geometrischen Abmessungen und einer materialspezifischen Konstante, dem spezifischen Widerstand ρ, berechnen.
Für einen in Längsrichtung durchflossenen geraden Leiter mit konstanter Querschnittsfläche A und der Länge l gilt:
Die Querschnittsfläche A berechnet sich für runde Drähte mit dem Durchmesser d nach der Formel:
Der spezifische Widerstand selbst ist im Allgemeinen von der Temperatur und eventuell noch weiteren Größen abhängig.
Temperaturabhängigkeit
Beispiele für spezifischen Widerstand und Temperaturkoeffizient bei 20 °C Material ρ20 in (Ω·mm²)/m α20 in 1/K Silber 1,587 · 10−2 3,8 · 10−3 Kupfer 1,786 · 10−2 3,9 · 10−3 Silizium 2,3 · 109 −7,5 · 10−2 Der elektrische Widerstand eines Leiters ist im Wesentlichen von seiner Temperatur und der Frequenz der Spannung abhängig.
Die Frequenzabhängigkeit kann man leicht umgehen, wenn man Gleichstrom verwendet. Dafür wird auch der Begriff Gleichstromwiderstand verwendet. Wie oben beschrieben, berechnet sich der Gleichstromwiderstand eines geraden Leiters durch:
Dieses gilt aber nur für die Temperatur, für die der angegebene spezifische Widerstand gilt. Wenn nicht anders angegeben, gilt dieses für eine Ausgangstemperatur von 20 °C. Darauf weist auch die 20 im Index von R hin.
Grundsätzlich ist aber der Widerstand temperaturabhängig. Dieses gilt für alle Materialien.
Dieses Verhalten ist materialabhängig und wird mit dem Linear-Temperaturkoeffizienten α und der Bestimmung des Temperaturunterschieds (ΔT = T − T0) berechenbar. Im allgemeinen beschreibt man diese Änderung durch eine Linearisierung
bei
Für die meisten Materialien und Anwendungen mit nicht zu großen Temperaturbereichen reicht diese lineare Näherung aus, da die Temperaturkoeffizienten höherer Ordnungen dann vernachlässigbar klein sind.
Je nachdem, ob der Widerstandswert mit steigender Temperatur größer oder kleiner wird, unterscheidet man zwischen Kaltleitern oder PTC (Widerstandswert steigt, prinzipiell bei allen Metallen; PTC: positive temperature coefficient) und Heißleitern oder NTC (Widerstandswert sinkt; NTC: negative temperature coefficient).
In der Technik wird die Temperaturabhängigkeit des elektrischen Widerstandes ausgenutzt, zum Beispiel beim Thermostaten und Widerstandsthermometer (Beispiel: Thermometer mit Pt100-Fühlern) oder bei Thermo-Anemometern (Windmessgeräten).
Es gibt auch verschiedene spezielle Metall-Legierungen, die sich durch einen über weite Temperaturbereiche annähernd konstanten spezifischen elektrischen Widerstand auszeichnen, → Messwiderstand.
Wechselstromwiderstand
Darstellung
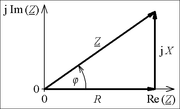
An einem linearen, rein ohmschen Widerstand R, der von Wechselstrom durchflossen wird, sind Spannung und Strom in Phase. Wenn allerdings eine frequenzabhängige Phasenverschiebung und Widerstandsänderung auftritt, kommt als Anteil am Widerstand eine Komponente X hinzu, die auf Spannungs- bzw. Stromänderungen verzögernd reagiert. Bei sinusförmigem Verlauf von Spannung und Strom wird der Quotient aus den Amplituden oder Effektivwerten als Scheinwiderstand Z bezeichnet. In der komplexen Wechselstromrechnung wird der Scheinwiderstand mit dem Phasenverschiebungswinkel
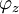 als Impedanz oder komplexer Widerstand
als Impedanz oder komplexer Widerstand 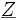 zusammengefasst.
zusammengefasst.In einer anderen Darstellung werden die zwei Komponenten zueinander rechtwinklig zu
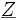 zusammengefasst,
zusammengefasst,Darin werden R als Wirkwiderstand und X als Blindwiderstand bezeichnet. Der Wirkwiderstand, welcher nicht phasenverschiebend arbeitet, wird auch als ohmscher Anteil der Impedanz bezeichnet.
Umrechnungen
Werden die Spannung
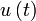 und der Strom
und der Strom 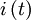 als sinusförmige Größen mit der Frequenz f bzw. der Kreisfrequenz ω = 2πf in der komplexen Ebene durch Zeiger
als sinusförmige Größen mit der Frequenz f bzw. der Kreisfrequenz ω = 2πf in der komplexen Ebene durch Zeiger 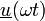 und
und 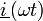 dargestellt, so erhält man
dargestellt, so erhält manmit
Durch Vergleich der beiden Darstellungen von
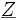 erhält man
erhält manEs ergeben sich der Scheinwiderstand:
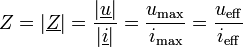
- oder
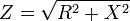
und der Phasenverschiebungswinkel zwischen
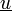 und
und 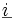 :
:Man bezeichnet auch
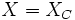 = kapazitiver Blindwiderstand
= kapazitiver Blindwiderstand
oder
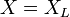 = induktiver Blindwiderstand.
= induktiver Blindwiderstand.
Wie weiter unter gezeigt wird, ist
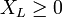 und
und 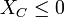 .
.
Sonderfälle
- Für R = 0 ergibt sich:
Für X > 0 ist
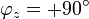 und
und 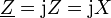 ;
;für X < 0 ist
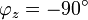 und
und 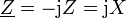 .
.- Für X = 0 ergibt sich:
Ursachen der komplexen Widerstände
Bei einer Spule mit der Induktivität L gilt
Aufgrund einer Spannung wächst der Strom mit der Zeit an. Bei Wechselstrom folgt dieser verzögert.
Mit dem Ansatz in komplexer Schreibweise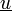 und
und 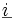 wie oben erhält man nach der Differenziation
wie oben erhält man nach der DifferenziationDas bedeutet, dass eine Induktivität für sinusförmige Wechselgrößen wie ein phasendrehender Blindwiderstand wirkt. Mit
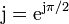 ergibt sich
ergibt sich 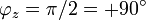 .
.Entsprechend gilt bei einem Kondensator mit der Kapazität C
Aufgrund eines Stromes wächst die Spannung mit der Zeit an. Bei Wechselspannung folgt diese verzögert.
Man erhält in komplexer Schreibweise und nach der IntegrationDas bedeutet, dass eine Kapazität für sinusförmige Wechselgrößen wie ein phasendrehender Blindwiderstand wirkt. Hier ist
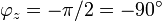 .
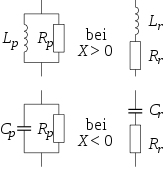
.Tatsächlich auftretende Wechselstromwiderstände beschreibt man durch Ersatzschaltbilder in Reihenschaltung oder Parallelschaltung aus einem ohmschen Widerstand mit einer Induktivität oder mit einer Kapazität. Welches der Bilder verwendet wird, ist eine Frage der besseren Annäherung an die Wirklichkeit mit möglichst frequenzunabhängigen Größen und der Zweckmäßigkeit für die mathematische Behandlung.
Bei genauer Betrachtung hat aber auch jeder Kondensator einen kleinen induktiven Anteil, so wie eine Spule auch einen kapazitiven Anteil hat. Selbst ein Stück Draht muss exakt mit R, C und L beschrieben werden. Dies zeigt sich dann im Besonderen, wenn die Bauteile mit ihren geometrischen Abmessungen in den Bereich der Wellenlänge der angelegten Wechselspannung kommen, dann besitzen sie einen nicht zu vernachlässigenden sowohl induktiven, als auch einen kapazitiven Anteil. Sie werden gegebenenfalls zum Schwingkreis, als Beispiel sei hier die Antenne genannt. Die Enden dürfen als Kondensatorplatten gesehen werden, der „Draht“ dazwischen als Spule.
Zusammenschaltung
Werden ein ohmscher Widerstand und eine Impedanz zusammengeschaltet, so können in komplexer Schreibweise die weiter unten folgenden Regeln für Reihen- und Parallelschaltung angewendet werden.
Werden eine kapazitive und eine induktive Impedanz zusammengeschaltet, so entsteht ein Schwingkreis; die Reihen- und Parallelschaltung und die weiteren Konsequenzen werden unter diesem Stichwort behandelt.
Ersatzwiderstand
Als Ersatzwiderstand wird der komplexe elektrische Widerstand bezeichnet, der den gleichen Widerstand besitzt wie eine elektrische Schaltung oder der Teil einer elektrischen Schaltung, den er ersetzt. Ersatzwiderstände können zur Vereinfachung der Berechnung komplexer elektrischer Anordnungen verwendet werden.
Ortskurve
Ein anschauliches Hilfsmittel zur Analyse und Beschreibung von Schaltungen mit Wechselstromwiderständen ist die Ortskurve.
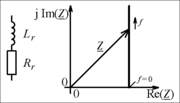
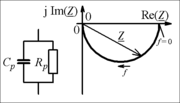
Komplexe Größen lassen sich durch Zeiger in der komplexen Ebene darstellen. Wenn die komplexe Größe eine Funktion eines (reellen) Parameters ist und wenn dieser Parameter variiert wird, verschiebt sich die Spitze des Zeigers. Eine Linie durch alle denkbaren Zeigerspitzen bezeichnet man als Ortskurve.
Die Bilder zeigen Ortskurven der Impedanz als Funktion der Frequenz für die angegebenen Schaltungen.
Der elektrische Widerstand im Teilchenmodell
Die physikalische Beschreibung benutzt die Vorstellung, dass sich die Valenzelektronen im Metall wie ein Gas (Elektronengas) verhalten. Im einfachsten Modell bildet das Metall ein positiv homogen geladenes Volumen, in denen sich die Elektronen frei bewegen können. In dieses Volumen sind die Atomrümpfe eingebettet, die aus dem Atomkern und den stärker gebundenen Elektronen auf den tieferen, vollbesetzten Schalen bestehen.
Ohne äußere elektrische Spannung bewegen sich die Elektronen ungeordnet im Metall (siehe: brownsche Bewegung). Legt man nun eine Spannung an die zwei Seiten an, so werden die freien Elektronen durch das elektrische Feld in Richtung der Feldlinien beschleunigt. Es fließt ein elektrischer Strom.
Auf ihrem Weg durch das Metall kommt es zu elastischen Stößen der Elektronen mit anderen Elektronen, den Atomrümpfen und Phononen. Dabei geben die Elektronen Energie an ihre Stoßpartner ab, werden gestreut und wieder durch das elektrische Feld beschleunigt. Die Elektronen werden durch diese Wechselwirkung dauernd abgebremst und es stellt sich eine mittlere Strömungsgeschwindigkeit ein.
Die bei diesen Stößen an die Atomrümpfe beziehungsweise Phononen übertragene Energie führt zu einer größeren Eigenschwingung um ihre Gleichgewichtslage, ihre Temperatur erhöht sich. Durch die stärkeren Schwingungen erhöht sich die Querschnittsfläche für mögliche Stöße, deren Anzahl mit steigender Temperatur zunimmt und den Widerstand steigen lässt (Kaltleiter). Der Leitungsvorgang in Heißleitern kann mit diesem Modell nicht vollständig erklärt werden, da es hier mit steigender Temperatur zu einer deutlichen Ladungsträgergeneration kommt, die den eben beschriebenen Vorgang überlagern.
Bei sehr hohen Temperaturen, bei denen die Atome des Materials ionisiert werden (Plasma), ist jeder Stoff elektrisch leitend, da die vorher gebundenen Elektronen nun für den Ladungstransport zur Verfügung stehen. Umgekehrt sind Metalle und Oxide bekannt, für die der elektrische Widerstand bei sehr niedrigen Temperaturen unterhalb der so genannten Sprungtemperatur verschwindet: Supraleiter.
Durch die thermische Bewegung der Elektronen entsteht ein temperaturabhängiger Rauschstrom, der als Widerstandsrauschen bezeichnet wird.
Reihen- und Parallelschaltung
Reihenschaltung
Werden n Widerstände in Reihe geschaltet, so addieren sich die Widerstände:
Veranschaulichen kann man sich dieses an zwei Widerständen, die sich nur in der Länge unterscheiden.
Die Reihenschaltung ergibt einen Widerstandskörper der Länge l1 + l2. Dann gilt:
Parallelschaltung
Bei der Parallelschaltung von n Widerständen addieren sich die Leitwerte beziehungsweise die reziproken Widerstände:
alternative Schreibweise:
Formel für zwei parallele Widerstände:
Schreibweise als Leitwerte:
Der Leitwert ist der Kehrwert des Widerstandes, seine SI-Einheit ist das reziproke Ohm, das auch den besonderen Namen Siemens führt.
Man veranschaulicht sich diesen Zusammenhang an der Parallelschaltung zweier Widerstände, die sich nur in ihrer Querschnittsfläche A unterscheiden.
Man erhält einen Widerstand vom Gesamtquerschnitt A1 + A2, also gilt:
und daher
Sind in einer Parallelschaltung nur Widerstände eines gleichen Wertes vorhanden, (
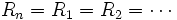 ) so kann der Gesamtwiderstand errechnet werden, indem man den Einzelwiderstand durch die Anzahl der Widerstände in der Schaltung dividiert:
) so kann der Gesamtwiderstand errechnet werden, indem man den Einzelwiderstand durch die Anzahl der Widerstände in der Schaltung dividiert:Dabei bezeichnet Rn die Werte der Einzelwiderstände und n deren Anzahl.
Differentieller Widerstand
Bei nichtlinearen Strom-Spannungs-Kennlinien - wie zum Beispiel von Dioden - ist der Quotient für jedes Strom-Spannungspaar unterschiedlich. In diesem Fall gilt das ohmsche Gesetz nicht und man kann nicht von einem ohmschen Widerstand R sprechen. Kleine Spannungsänderungen sind jedoch näherungsweise proportional zu kleinen Stromänderungen. Der Quotient aus kleiner Spannungsänderung und zugehöriger Stromänderung bei einer bestimmten Spannung wird als differentieller Widerstand r bezeichnet. In einem Diagramm, in dem U über I aufgetragen wird, entspricht er der Steigung der Tangente am betrachteten Punkt der Kennlinie.
Negativer differentieller Widerstand
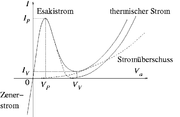
Der differentielle Widerstand kann in einem Teil der Kennlinie negativ sein, so dass die Stromstärke bei steigender Spannung sinkt beziehungsweise die Stromstärke bei sinkender Spannung steigt. Im Bild ist das im Bereich VP < V < VV der Fall. Ein negativer differentieller Widerstand kann zum Anregen (Entdämpfen) von Schwingkreisen oder zur Erzeugung von Kippschwingungen verwendet werden (Oszillator). Der negative differentielle Widerstand tritt zum Beispiel bei Gasentladungen, Bauteilen wie Avalanche- oder Tunneldioden auf, aber auch bei komplexeren Modulen wie z. B. Schaltnetzteilen auf der Eingangsseite.
Positiver differentieller Widerstand
Bei positiven differentiellen Widerständen nimmt der Widerstand mit zunehmender Spannung zu. Alle real existierenden Schaltungselemente besitzen in einem Teil ihrer Kennlinie, jedoch stets für sehr große Werte, einen positiven differentiellen Widerstand. Die meisten Elemente in der Schaltungstechnik besitzen einen ausschließlich positiven differentiellen Widerstand.
Beispiele: realer Widerstand, Diode, Zener-Diode, alle halbleitenden Keramiken.
Supraleitung
Unterhalb einer spezifischen Sprungtemperatur besitzt ein supraleitungsfähiges Material praktisch keinen ohmschen Widerstand. Ein solches Material wird als Supraleiter bezeichnet, weil der Strom in ihm bei dieser tiefen Temperatur ohne Verluste fließt.
Weblinks
Einzelnachweise
- ↑ Georg Simon Ohm: Die galvanische Kette. [Reprint der Ausg., [Riemann], 1827] Oekonomie-Verl. Müller im VDM, Saarbrücken 2006, ISBN 3939962031
Wikimedia Foundation.

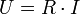
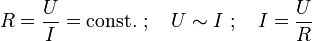
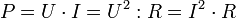
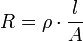
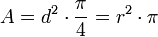
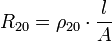
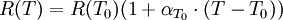
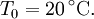
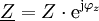
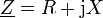
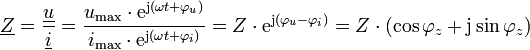
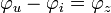
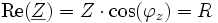 (
(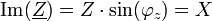 (
(