- Rechteckverteilung
-
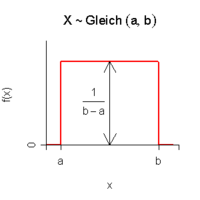
Die stetige Gleichverteilung, auch Rechteckverteilung oder Uniformverteilung genannt, ist eine stetige Wahrscheinlichkeitsverteilung. Sie hat auf einem Intervall (a,b) eine konstante Wahrscheinlichkeitsdichte. Dies ist gleichbedeutend damit, dass alle Teilintervalle gleicher Länge dieselbe Wahrscheinlichkeit besitzen.
Inhaltsverzeichnis
Definition
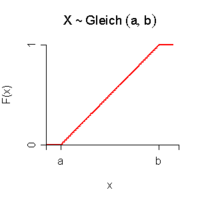
Eine stetige Zufallsvariable X bezeichnet man als gleichverteilt auf dem Intervall [a,b], wenn Wahrscheinlichkeitsdichte f(x) und Verteilungsfunktion F(x) gegeben sind als
Als abkürzende Schreibweise für die stetige Gleichverteilung wird häufig
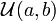 oder
oder 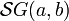 verwendet.
verwendet.Eigenschaften
Erwartungswert und Median
Der Erwartungswert und der Median der stetigen Gleichverteilung ist
Varianz
Die Varianz der stetigen Gleichverteilung ist
Standardabweichung
Aus der Varianz erhält man die Standardabweichung
Variationskoeffizient
Für den Variationskoeffizienten ergibt sich:
Schiefe
Die Schiefe lässt sich darstellen als
Wölbung
Die Wölbung lässt sich ebenfalls geschlossen darstellen als
Summe von gleichverteilten Zufallsvariablen
Die Summe zweier unabhängiger und stetig gleichverteilter Zufallsvariablen ist dreiecksverteilt.
Charakteristische Funktion
Die charakteristische Funktion hat die Form
wobei i die imaginäre Einheit darstellt.
Momenterzeugende Funktion
Die momenterzeugende Funktion der stetigen Gleichverteilung ist
und speziell für a = 0 und b = 1
Damit ergeben sich die ersten allgemeinen Momente zu
Beziehung zu anderen Verteilungen
Mit der Inversionsmethode lassen sich gleichverteilte Zufallszahlen in andere Verteilungen überführen. Wenn X eine gleichverteilte Zufallsvariable ist, dann genügt beispielsweise
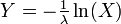 der Exponentialverteilung mit dem Parameter λ.
der Exponentialverteilung mit dem Parameter λ.Beispiel für das Intervall [0,1]
Häufig wird a = 0 und b = 1 angenommen. Dann ist:
- f(x) = 1 für
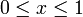
- F(x) = x für
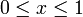
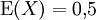
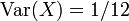
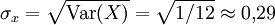
Ein Beispiel für eine auf dem Intervall [0,1] stetig gleichverteilte Zufallsvariable ist die Funktion Z(y) = y. Hier ist offenbar
daher ist Z gleichverteilt.
Siehe auch
Weblinks
- Universität Konstanz – Interaktive Animation
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.

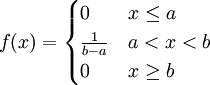
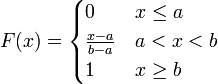
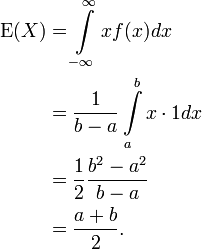
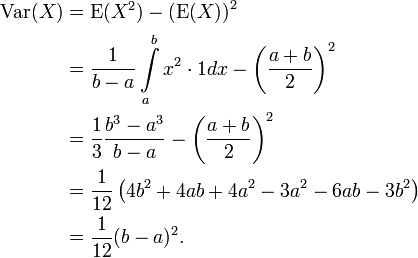
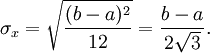
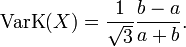
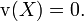
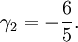
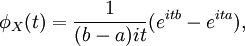
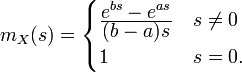
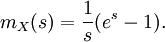
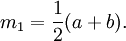
![\mathbb{P} (Z \leq x)= \mathbb{P} ([-\infty,x])=F(x)=\begin{cases}
0 & x \le 0\\
x & 0 < x < 1\\
1 & x\ge 1,
\end{cases}](/pictures/dewiki/54/61eafb92fdddd95fca8a282e3d0d51b7.png)