- Dodecaedron simum
-
Das abgeschrägte Dodekaeder (auch Dodecaedron simum genannt) ist ein Polyeder, das zu den Archimedischen Körpern zählt. Es setzt sich aus 92 Flächen, nämlich 12 regelmäßigen Fünfecken und 80 gleichseitigen Dreiecken, zusammen und hat 60 Ecken sowie 150 Kanten. Dabei bilden jeweils vier Dreiecke und ein Fünfeck eine Raumecke.
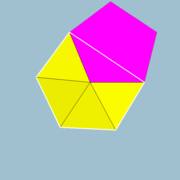
Die folgenden Bilder zeigen zwei zueinander spiegelbildliche abgeschrägte Dodekaeder.
Konstruktion
Wie der Name schon andeutet, entsteht dieses Polyeder durch fortwährendes Abschrägen eines Dodekaeders, sodass am Ende zwölf (kleinere) regelmäßige Fünfecke übrigbleiben, die koinzident mit den ursprünglichen Begrenzungsflächen des Dodekaeders sind.
Formeln
Nachfolgend bezeichne der Term t den Kosinus des kleineren Zentriwinkels ζ im Sehnenfünfeck (weiße Linien in der Grafik rechts) mit den Seitenlängen a und d = a·φ (d. i. die Diagonale im Pentagon; φ ist die Goldene Zahl). Dann ist t die einzige reelle Lösung der kubischen Gleichung
Mit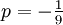 und
und 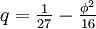 folgt somit nach den Cardanischen Formeln:
folgt somit nach den Cardanischen Formeln:Größen eines abgeschrägten Dodekaeders mit Kantenlänge a Oberflächeninhalt 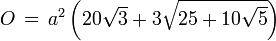
Volumen 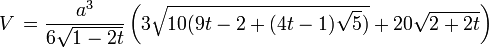
Umkugelradius 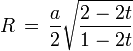
Kantenkugelradius 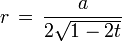
Flächen-Flächen-Winkel
≈ 164,18° (Trigon–Trigon)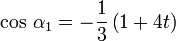
Flächen-Flächen-Winkel
≈ 152,93° (Pentagon–Trigon)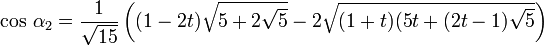
Flächen-Kanten-Winkel
≈ 143,35° (Pentagon–Trigon)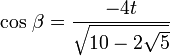
Kanten-Kanten-Winkel
≈ 118,14° (Trigon–Trigon)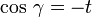
Weblinks
- Eric W. Weisstein: Snub Dodecahedron auf MathWorld (engl.)
Tetraederstumpf · Kuboktaeder · Hexaederstumpf · Oktaederstumpf · Rhombenkuboktaeder · Großes Rhombenkuboktaeder · Dodekaederstumpf · Ikosaederstumpf · Ikosidodekaeder · Abgeschrägtes Hexaeder · Rhombenikosidodekaeder · Großes Rhombenikosidodekaeder · Abgeschrägtes Dodekaeder
Rhombendodekaeder · Triakistetraeder · Triakisoktaeder · Tetrakishexaeder · Deltoidalikositetraeder · Pentagonikositetraeder · Rhombentriakontaeder · Hexakisoktaeder · Triakisikosaeder · Pentakisdodekaeder · Deltoidalhexakontaeder · Pentagonhexakontaeder · Disdyakistriakontaeder
Wikimedia Foundation.




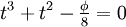
![t = cos(\zeta) = - \tfrac{1}{3} + \sqrt[3]{-q + \sqrt{q^2+p^3}} + \sqrt[3]{-q - \sqrt{q^2+p^3}}](/pictures/dewiki/100/d62799e687a39776dd542f4c4b496ca0.png)