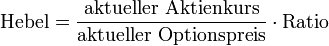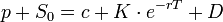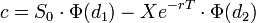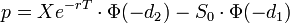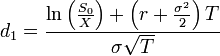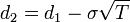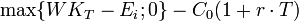Finanzoption

Eine Option bezeichnet in der Wirtschaft ein abgeleitetes Finanzgeschäft (so genanntes Derivat). Mit einer Option erhält man das Recht, ein Wertpapier oder ein anderes Produkt zu einem späteren Zeitpunkt zu einem vorher vereinbarten Preis zu kaufen oder zu verkaufen. Es muss also nicht „unbedingt“ ge- oder verkauft werden, sondern man kann die Option auch verfallen lassen. Das Optionsgeschäft ist eine besondere Form des Termingeschäfts und wird auch als „bedingtes Termingeschäft“ bezeichnet.

In der Praxis muss der Basiswert bei Ausübung der Option auch nicht unbedingt geliefert werden. Häufig bezahlt der Verkäufer der Option dem Käufer oder umgekehrt einfach die Preisdifferenz. Diese Praxis wird als Barausgleich bezeichnet. Ob bei Ausübung ein Barausgleich stattfindet oder ob der Basiswert geliefert wird, wird bei Vertragsabschluss festgelegt.

Merkmale von Optionen allgemein

Der Käufer erwirbt das Recht, hat aber nicht die Pflicht,

• während eines festgelegten Zeitraums (Kontraktlaufzeit, Lebenszeit) bei amerikanischen Optionen
• bzw. am Ende der Laufzeit zum Ausübungsdatum bei europäischen Optionen

die Option einzulösen.

Im Falle der Einlösung der Option erhält er einen Auszahlungsbetrag, der von allen möglichen Faktoren beeinflusst sein kann.

Der Verkäufer definiert genau, wie hoch die Auszahlung unter welchen Bedingungen ist.

Merkmale von Standard-Optionen

Die Standard-Optionen, auch Plain Vanilla Options genannt, sind Put-Optionen und Call-Optionen, sowohl amerikanischer als auch europäischer Art.

Der Käufer erwirbt das Recht, hat aber nicht die Pflicht,

• während eines festgelegten Zeitraums (Kontraktlaufzeit, Lebenszeit) bei amerikanischen Optionen
• bzw. am Ende der Laufzeit zum Ausübungsdatum bei europäischen Optionen

eine bestimmte Menge eines Gutes (Basiswert, Underlying oder underlying asset) zu einem im voraus festgelegten Preis (Ausübungspreis oder Strike-Preis)

• zu kaufen (Call-Option) oder
• zu verkaufen (Put-Option).

Der Verkäufer (auch Stillhalter, Schreiber, Zeichner) erhält den Kaufpreis der Option. Er ist im Falle der Ausübung verpflichtet, den Basiswert zum vorher bestimmten Preis zu kaufen (Put) bzw. zu verkaufen (Call).

Black-Scholes-Modell

Im Jahre 1973 veröffentlichten die amerikanischen Wissenschaftler Fischer Black und Myron Scholes fast zeitgleich mit Robert C. Merton in zwei unabhängigen Artikeln Methoden zur exakten Bestimmung des „wahren“ Wertes einer Option. Scholes und Merton erhielten 1997 den Preis der Schwedischen Reichsbank für Ökonomische Wissenschaften in Erinnerung an Alfred Nobel, oftmals als Wirtschaftsnobelpreis bezeichnet, „für eine neue Methode zur Bestimmung des Wertes von Derivaten“, das Black-Scholes-Modell. Black konnte den Preis nicht mehr entgegennehmen, er verstarb im August 1995.

Taxonomie verschiedener Optionen

Prinzipiell unterscheidet man anhand der Ausübungsart der Option zwischen der Amerikanischen Option und der Europäischen Option (die Asiatische Option ist keine nach der Ausübungsart abgegrenzte Optionsart, sondern als Option mit spezieller Wertermittlung zum Ausübungstag eine Exotische Option).

Europäische Optionen können nur am Ende der Laufzeit ausgeübt werden, Amerikanische Optionen zu jedem Zeitpunkt während ihrer Laufzeit. Dies beeinflusst den Wert der Option, beispielsweise durch das Vorhandensein von Dividenden im Falle von Aktienoptionen, und macht amerikanische Optionen teurer als eine europäische Option mit ansonsten identischen Merkmalen.

Optionen lassen sich noch weiter nach der zeitlichen Ausübbarkeit charakterisieren:

• So lässt sich bspw. das Optionsrecht von Wandelanleihen, sobald ein zukünftiger Zeitpunkt eingetreten ist, jederzeit ausüben. Wandelanleihen schließen das Recht auf Wandlung in Aktien sowie ein Kündigungsrecht für den Emittenten ein.
• Bermuda-Optionen beinhalten ein Kündigungsrecht zu bestimmten zukünftigen Zeitpunkten (zu einem festen Kupontermin unter Einhaltung einer beispielsweise dreimonatigen Kündigungsfrist). Diese Optionen heißen Bermuda, da sich die Inselgruppe der Bermudas zwischen Europa und Amerika befinden, genau wie sich die Ausübungstermine der Bermuda-Optionen zeitlich zwischen denen der europäischen- und amerikanischen Optionen bewegen.

Aus den beiden Grundformen, den plain vanilla options, können beliebig viele Optionen erstellt werden. Nichtstandardisierte Optionstypen nennt man exotische Optionen. Dazu gehören unter unzähligen anderen capped options, rainbow options, asian options und compound options.

Handel

Eine Option kann als ein individueller Vertrag zwischen dem Optionsnehmer und dem Optionsgeber (Stillhalter) abgeschlossen werden. Sie ist als solcher frei gestaltbar. Solche direkt zwischen zwei Vertragsparteien abgeschlossene Optionen nennt man gemeinhin OTC-Optionen.

Der größte Teil des weltweiten Handels mit Optionen besteht jedoch aus standardisierten Kontrakten, die an Terminbörsen wie der EUREX in Europa oder der CBOT in den USA gehandelt werden. Die Standardisierung soll die Liquidität der Optionen erhöhen.

Letztendlich können Optionen noch als Wertpapier gestaltet werden (Optionsschein).

Basiswerte

An den Finanzmärkten können Optionen auf folgende Basiswerte gehandelt werden

• Aktien
• Exchange-traded fund
• Indizes
• ausländische Währungen
• Anleihen
• Rohstoffe
• Nahrungsmittel
• elektrischer Strom
• Wetter
• andere Optionen

Für den geregelten Handel mit Optionen ist es Voraussetzung, dass die Basiswerte an liquiden Märkten gehandelt werden, um jederzeit den Wert der Option ermitteln zu können. Im Prinzip ist es jedoch auch möglich, dass der Basiswert beliebig gewählt werden kann, solange es möglich ist, die in Abschnitt 6 beschriebenen nötigen Variablen zu bestimmen. Diese Derivate werden hingegen nur von zugelassenen Händlern wie Investmentbanken oder Brokern over the counter im außerbörslichen Handel angeboten.

Begriffe

Im Geld

Im Geld (englisch in the money) bezeichnet eine Option, bei der der aktuelle Kurs höher ist als der Ausübungspreis (Call) bzw. der aktuelle Kurs niedriger ist als der Ausübungspreis (Put). Der Betrag, um den der aktuelle Kurs besser ist als der Ausübungspreis, nennt man Inneren Wert der Option.

1. Im Geld bedeutet für eine Call-Option, dass der Marktpreis des Basiswertes höher ist als der Ausübungspreis.
2. Eine Put-Option ist dagegen im Geld, wenn der Marktpreis des Basiswertes unter dem Ausübungspreis liegt.

Aus dem Geld

• Aus dem Geld (englisch out of the money) ist eine Option, die keinen inneren Wert besitzt
• Eine Call-Option ist aus dem Geld, wenn der Marktpreis des Basiswertes kleiner als der Ausübungspreis ist
• Eine Put-Option ist aus dem Geld, wenn der Marktpreis des Basiswertes größer als der Ausübungspreis ist

Am Geld

Eine Option ist am Geld (englisch at the money), wenn der Marktpreis des Basiswertes gleich oder nahezu gleich dem Ausübungspreis ist.

Wird der Ausübungspreis dabei mit dem Kassakurs verglichen, so spricht man von at-the-money-spot. Wird der Ausübungspreis mit dem laufzeitgleichen Terminkurs verglichen, so spricht man von at-the-money-forward.

Siehe hierzu auch: Moneyness.

Sensitivitäten und Kennzahlen - die sog. „Griechen“

Delta

Sensitivitätskennzahl, die angibt, welchen Einfluss der Preis des Basiswertes auf den Wert der Option hat. Das Delta ist mathematisch die erste Ableitung des Optionspreises nach dem Preis des Basiswertes. So bedeutet ein Delta von 0,5 dass eine Veränderung des Basiswertes um 1 Euro (in linearer Näherung) eine Veränderung des Optionspreises von 50 Cent hervorruft. Das Delta ist insbesondere im Zusammenhang mit dem sog. Delta-Hedging wichtig.

Gamma

Das Gamma einer Option gibt an, wie stark sich deren Delta (in linearer Näherung) ändert, wenn sich der Kurs des Basiswerts um eine Einheit ändert und alle anderen Größen sich nicht verändern. Mathematisch ist das Gamma die zweite Ableitung des Optionspreises nach dem Preis des Basiswertes. Für den Inhaber der Option (also sowohl für Long Call als auch für Long Put) gilt immer, dass Gamma ≥ 0 ist. Die Kennzahl findet auch bei Absicherungsstrategien in Form des Gamma-Hedging Berücksichtigung.

Theta

Das Theta einer Option gibt an, wie stark sich der theoretische Wert einer Option ändert, wenn sich die Restlaufzeit um einen Tag verkürzt und alle anderen Größen konstant bleiben. Für den Inhaber der Option ist das Theta normalerweise negativ, eine kürzere Restlaufzeit bedeutet also immer einen geringeren theoretischen Wert.

Vega

Das Vega (manchmal auch Lambda, da Vega kein Buchstabe des griechischen Alphabets ist) einer Option gibt an, wie stark sich der Wert der Option ändert, wenn sich die Volatilität des Basiswerts um einen Prozentpunkt ändert und alle anderen Größen konstant bleiben.

Rho

Das Rho einer Option gibt an, wie stark sich der Wert der Option ändert, wenn sich der risikofreie Zinssatz am Markt um einen Prozentpunkt ändert. Für Call-Optionen ist Rho positiv, für Put-Optionen negativ.

Hebel

Der Hebel wird errechnet, indem man den aktuellen Kurs des Basiswerts durch den aktuellen Preis der Option dividiert. Bezieht sich die Option auf ein Vielfaches oder einen Bruchteil des Basiswerts, muss dieser Faktor in der Rechnung entsprechend berücksichtigt werden. Man spricht hierbei vom Bezugsverhältnis.

• $\text{Hebel} = \frac{\text{aktueller Aktienkurs}}{\text{aktueller Optionspreis}} \cdot \text{Ratio}$

Omega

Man erhält durch Multiplikation des Deltas mit dem aktuellen Hebel eine neue Hebelgröße, die sich in den Kurstabellen meist unter der Bezeichnung Omega oder „Hebel effektiv“ findet. Eine Option mit einem aktuellen Hebel von 10 und einem Delta von 50% hat also „nur“ ein Omega von 5, der Schein steigt also etwa um 5%, wenn die Basis um 1% steigt. Auch hier ist jedoch wieder zu beachten, dass sowohl das Delta und das Omega und die meisten anderen Kennzahlen sich ständig ändern. Trotzdem bietet das Omega ein relativ gutes Bild von den Chancen der entsprechenden Option.

Bewertung

Einflussgrößen

Der Preis einer Option hängt zum einen von ihren Ausstattungsmerkmalen ab, hier

• der aktuelle Preis des Basiswerts,
• der Ausübungspreis,
• die Restlaufzeit bis zum Ausübungsdatum,

zum anderen von dem zugrunde gelegten Modell für die zukünftige Entwicklung des Basiswertes und anderer Marktparameter. Unter dem Black-Scholes-Modell sind die weiteren Einflussgrößen

• die Volatilität des Basiswerts,
• der risikofreie, kurzfristige Zinssatz am Markt,
• erwartete Dividendenzahlungen innerhalb der Lebenszeit.

Der aktuelle Preis des Basiswertes und der Ausübungspreis bestimmen den inneren Wert der Option. Der innere Wert ist die Differenz zwischen dem Ausübungspreis und dem Preis des Basiswertes. Im Falle eines Calls auf einen Basiswert mit einem augenblicklichen Wert von 100,- € und einem Ausübungspreis von 90,- € ist der innere Wert 10,- €. Im Falle eines Puts ist der innere Wert dieser Option 0.

Insbesondere die Volatilität hat einen großen Einfluss auf den Wert der Option. Je stärker der Preis schwankt, umso höher ist die Wahrscheinlichkeit, dass sich der Wert des Basiswertes stark verändert und damit der innere Wert der Option steigt oder sinkt. In der Regel gilt, dass eine höhere Volatilität einen positiven Einfluss auf den Wert der Option hat. In extremen Grenzfällen kann es sich jedoch genau umgekehrt verhalten.

Die Restlaufzeit beeinflusst den Wert der Option ähnlich wie die Volatilität. Je mehr Zeit bis zum Ausübungsdatum vorhanden ist, um so höher ist die Wahrscheinlichkeit, dass sich der innere Wert der Option ändert. Ein Teil des Wertes der Option besteht aus diesem Zeitwert. Es ist theoretisch möglich, den Zeitwert zu berechnen, indem man zwei Optionen vergleicht, die sich nur durch ihre Laufzeit unterscheiden und ansonsten identisch sind. Dies setzt aber den unrealistischen Fall eines nahezu vollkommenen Kapitalmarkts voraus.

Der Anstieg des risikofreien Zinssatzes hat einen positiven Effekt auf den Wert von Kaufoptionen (Calls) und einen negativen Effekt auf den Wert von Verkaufsoptionen (Puts), weil nach den gängigen Bewertungsmethoden die Wahrscheinlichkeit eines Kurs- oder Wertanstiegs des Basisguts an den risikofreien Zinssatz gekoppelt ist. Das liegt daran, dass das Geld, das dank des Calls nicht in einen Basiswert investiert werden muss, zinsbringend angelegt werden kann. Je höher die Zinsen einer alternativen Geldanlage sind, desto attraktiver ist der Kauf eines Calls. Mit steigendem Zinsniveau steigt damit der über den Inneren Wert hinausgehende Wert der Option, der Zeitwert. Beim Put ist die Situation umgekehrt: Je höher das Zinsniveau, desto niedriger ist der Zeitwert des Puts, weil man theoretisch den Basiswert der Option besitzen müsste, um das Verkaufsrecht in Anspruch nehmen zu können.

Dividendenzahlungen im Falle von Optionen auf Aktien haben negativen Einfluss auf den Wert einer Kaufoption im Vergleich zur selben Aktie bei Dividendenlosigkeit, da während der Optionshaltedauer auf Dividenden verzichtet wird, die theoretisch durch Ausübung der Option vereinnahmt werden können. Umgekehrt haben sie im Vergleich zur selben dividendenlosen Aktie einen positiven Einfluss auf den Wert einer Verkaufsoption, weil während der Optionshaltedauer noch Dividenden vereinnahmt werden können, die bei sofortiger Ausübung dem Optionsinhaber zuständen. Im Falle von Optionen auf Währungen oder Rohstoffe wird der zugrunde liegende Zinssatz der Währung oder die 'convenience yield' anstelle von Dividenden verwendet.

Asymmetrischer Gewinn und Verlust

Im Falle einer für ihn nachteiligen Entwicklung im Preis des Basiswertes wird der Besitzer der Option sein Recht nicht ausüben und die Option verfallen lassen. Er verliert damit maximal den Optionspreis - d.h. er realisiert einen Totalverlust! -, hat aber die Möglichkeit auf einen unbegrenzten Gewinn bei Kaufoptionen. Dies bedeutet, dass die möglichen Verluste des Verkäufers bei Kaufoptionen unbegrenzt sind. Allerdings könnte man diesen Verlust auch als 'entgangenen Gewinn' (gedeckter Short-Call) betrachten, es sei denn, der Verkäufer der Kaufoption ist nicht im Besitz der entsprechenden Basiswerte (muss also zur Erfüllung kaufen und dann liefern - ungedeckter Verkauf einer Kaufoption (ungedeckter Short-Call), wobei ungedeckt bedeutet, dass die Position nur aus einem Instrument besteht.).

Die folgenden Grafiken verdeutlichen die asymmetrische Auszahlungsstruktur. Die dargestellten Optionen sind identisch in allen Einflussgrößen. Wichtig für das Verständnis ist, dass der Käufer einer Option eine long position eingeht und der Verkäufer einer Option eine short position eingeht. In allen vier Fällen ist der Wert der Option 10 und der Ausübungspreis 100.

In der vorherigen Grafik ist zu sehen, dass der Käufer (long) des Calls einen maximalen Verlust von 10 hat, hingegen unbegrenzte Gewinnmöglichkeiten besitzt. Im Gegensatz dazu hat der Verkäufer (short) einen maximalen Gewinn von 10 mit unbegrenzten Verlusten.

Im Falle eines Puts hat der Käufer (long) ebenfalls einen maximalen Verlust von 10. Ein häufiger Fehler ist die Übertragung der unbegrenzten Gewinnmöglichkeit der Kaufoption auf die Verkaufsoption. Das Basisgut kann aber allenfalls den Kurswert null annehmen. Dadurch ist die maximale Gewinnmöglichkeit auf diesen Fall eines Kurses von null begrenzt. Genau wie beim Call hat der Verkäufer (short) einen maximalen Gewinn von 10 mit nunmehr nur begrenzten Verlusten, wenn der Kurs des Basiswerts null annimmt. Der Unterschied zwischen Call und Put liegt darin, wie sich die Auszahlung im Verhältnis zum Basiswert verändert, und in der Begrenzung des Maximalgewinns/-verlusts bei Verkaufsoptionen.

Berechnung des Optionspreises

In der Optionspreistheorie gibt es prinzipiell zwei Herangehensweisen zur Bestimmung des fairen Optionspreises:

• Mit Hilfe von Abschätzungen ohne Annahmen über mögliche zukünftige Aktienkurse und deren Wahrscheinlichkeiten (Verteilungsfreie No-Arbitrage-Beziehungen, Siehe: Optionspreistheorie)
• Durch mögliche Aktienkurse und risikoneutrale Wahrscheinlichkeiten. Hierzu zählen das Binomialmodell sowie das Black-Scholes-Modell

Prinzipiell ist es möglich, die stochastischen Prozesse, welche den Preis des Basiswertes bestimmen, auf unterschiedliche Weise zu modellieren. Man kann diese Prozesse analytisch zeitkontinuierlich mit Differentialgleichungen und analytisch zeitdiskret mit Binomialbäumen abbilden. Eine nichtanalytische Lösung ist durch Zukunftssimulationen möglich.

Das bekannteste analytisch zeitkontinuierliche Modell ist das Modell von Black und Scholes. Das bekannteste analytisch zeitdiskrete Modell ist das Cox-Ross-Rubinstein-Modell. Eine gängige Simulationsmethode ist die Monte-Carlo-Simulation.

Verteilungsfreie No-Arbitrage-Beziehungen

Siehe Hauptartikel Optionspreistheorie

Eine Call-Option kann nicht mehr wert sein als der Basiswert. Angenommen, der Basiswert wird heute zu 80,- € gehandelt und jemand bietet auf diesen Basiswert eine Option an, die 90,- € kostet. Niemand würde diese Option kaufen wollen, weil der Basiswert selbst günstiger zu erwerben ist, der offensichtlich mehr wert ist als die Option. Da z.B. eine Aktie als Basiswert keine Verpflichtungen beinhaltet, kann diese gekauft und deponiert werden. Bei Bedarf wird sie wieder hervorgeholt. Dies entspricht einer ewigen Option mit Ausübungskurs 80,- €; eine wertvollere Option ist aber nicht denkbar, so dass die (Call-)Option nie wertvoller sein kann als der Basiswert.

Eine Put-Option kann nicht mehr wert sein als der Barwert des Ausübungspreises. Niemand würde für das Recht, etwas für 80,- € verkaufen zu dürfen, mehr als 80,- € ausgeben. Finanzmathematisch korrekt müssen diese 80,- € auf den heutigen Barwert abgezinst werden.

Diese Wertgrenzen sind der Ausgangspunkt zur Bestimmung des Wertes einer europäischen Option, die Put-Call Parität.

Put-Call-Parität

Die Put-Call-Parität ist eine Beziehung zwischen dem Preis eines europäischen Calls und dem Preis eines europäischen Puts, wenn beide den gleichen Basispreis und das gleiche Fälligkeitsdatum haben:

• $p + S_0 = c + K \cdot e^{-rT} + D$

wobei

• p: Preis der europäischen Verkaufsoption
• S₀: Aktienkurs
• c: Preis der europäischen Kaufoption
• K: Basispreis der Kauf- und Verkaufsoption
• r: risikoloser Zinssatz
• D: Diskontierte Dividendenzahlungen während der Laufzeit der Optionen

Mittels der Put-Call-Parität lässt sich die Äquivalenz zwischen Optionsstrategien und einfachen Optionspositionen zeigen.

• Covered Call entspricht Put short, an diesem Beispiel Beziehung demonstriert: S₀ − c = Ke ^{− rT} + D − p, d. h. Aktie long und Call short (=Covered Call) ist gleich einem Put short zuzüglich eines Geldbetrages
• Gegenposition (Reverse Hedge) von Covered Call entspricht Put long
• Protective Put entspricht Call long
• Gegenposition von Protective Put entspricht Call short

Black-Scholes

Siehe Hauptartikel Black-Scholes-Modell

Die Black-Scholes-Formeln für den Wert europäischer Calls und Puts auf Basiswerte ohne Dividendenzahlungen sind

• $c=S_0 \cdot \Phi(d_1)-Xe^{-rT} \cdot \Phi(d_2)$
• $p=Xe^{-rT} \cdot \Phi(-d_2)-S_0 \cdot \Phi(-d_1)$

wobei

• $d_1 = \frac{\ln \left (\frac{S_0}{X} \right)+ \left(r+ \frac{\sigma^2}{2} \right)T} {\sigma\sqrt{T}}$
• $d_2=d_1-\sigma\sqrt{T}$

In dieser Formel ist S der heutige Preis des Basiswertes, X der Ausübungspreis, r der risikolose Zinssatz, T die Lebenszeit der Option in Jahren, σ die Volatilität von 'S' und Φ(x) die kumulative Wahrscheinlichkeit, dass eine Variable mit einer Standardnormalverteilung 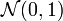$\mathcal N(0,1)$ kleiner als x ist.

Die Formel für c gibt auch den Wert einer amerikanischen Call Option mit denselben Kennzahlen unter der Annahme, dass der Basiswert keine Dividenden zahlt. Es existiert keine analytische Lösung für den Wert einer amerikanischen Put-Option.

Berücksichtigung von Zinsen

Der Gewinn bzw. Verlust von Optionen lässt sich unter Berücksichtigung von Zinsen bestimmen als:

• $\max \{ WK_T - E_i ; 0 \} - C_0(1+r \cdot T)$

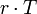wobei $r \cdot T$ linear ist, da hier der Geldmarktzinssatz verwendet wird.

Verwässerungsschutz

Bei den Bewertungsmethoden wird implizit angenommen, dass das Optionsrecht nicht durch Kapitalmaßnahmen der Aktiengesellschaft an Wert verlieren (verwässern) kann. Dies wird durch den sog. Verwässerungsschutz beim Optionshandel gewährleistet.

Optimale Ausübung

Amerikanische Optionen lassen sich zu mehreren Zeitpunkten ausüben. Das Ausübungsverhalten wird beeinflusst von den Faktoren Zinsen auf Basispreis, einen Flexibilitätseffekt und der Dividende. Zu differenzieren ist nach Calls und Puts.

Ein positiver Effekt bedeutet, dass ausgeübt werden soll, ein negativer Effekt, dass es lohnender ist abzuwarten.

Bei Zinsen auf den Basispreis ist der Effekt auf Calls negativ, auf Puts dagegen positiv. Der Flexibilitätseffekt wirkt sowohl negativ auf Calls wie auch auf Puts. Das Dividendenereignis hat einen positiven Effekt auf Calls, jedoch einen negativen auf Puts.

Dividenden

• Wird keine Dividende gezahlt, so ist die Ausübung eines Calls am Ende der Laufzeit immer optimal.
• Bei Dividendenzahlung ist das Abwarten bis zum Endtermin für Puts weiterhin optimal.

Kritik zu den Standardbewertungsmethoden

Üblicherweise basieren die Bewertungsmethoden auf den Annahmen, dass die Wertänderungen normalverteilt („Glockenkurve“) sowie voneinander unabhängig sind. Nach Benoît Mandelbrot sind alle darauf aufbauenden Modelle und Bewertungsformeln (z.B. die obige von Black/Scholes) falsch. Seine Untersuchungen ergaben, dass die Kursänderungen exponentiell verteilt und voneinander abhängig sind und damit zu wesentlich heftigeren Preisausschlägen führen, als die Standardmodelle vorsehen. Die Nobelpreisträger Merton und Scholes haben z.B. mit ihrem Hedgefonds LTCM eine spektakuläre Pleite hingelegt, als die Anleihemärkte wegen der Russlandkrise in sehr starke Turbulenzen gerieten. Nach ihrer Theorie hätten derartige Kurssprünge gar nicht auftreten dürfen.

Kritik des orthodoxen Optionsverständnisses

Der US-amerikanische Finanzmarktfachmann Nasser Saber (z.B. 2006) hält den Begriff „Option“ für nicht hilfreich, weil die Ausübung oder Nichtausübung immer stattfinden wird, wenn die entsprechenden Umstände eingetreten sind. Man sagt ja auch nicht, dass der Käufer einer Ware dem Verkäufer die „Option“ einräumt, den Kaufpreis anzunehmen oder auch nicht. In einer heterodoxen Sichtweise versteht Saber unter Option ein Termingeschäft, bei dem eine Seite das Recht auf Nichterfüllung (right to default) ihrer Zahlungverpflichtung kauft.

So zahlt bei einem normalen Termingeschäft „Short“ an „Long“, wenn der Preis steigt, und umgekehrt „Long“ an „Short“, wenn der Preis fällt.

Wenn Long durch Bezahlen einer Prämie (Preis der Option) an Short sich das Recht kauft, dass er bei diesem Termingeschäft nicht zahlen muss, wenn der Preis fällt, liegt eine Call-Option vor. Wenn Short durch Bezahlen einer Prämie (Preis der Option) an Long sich das Recht kauft, dass er bei diesem Termingeschäft nicht zahlen muss, wenn der Preis steigt, liegt eine Put-Option vor.

Die auf Grundlage dieser Vorstellung ermittelten Optionspreise stimmen mathematisch, nach Saber aber nicht inhaltlich, mit denen der Black-Scholes-Methode überein.

Ein Zahlenbeispiel

Berechnung des Preises einer Call-Option nach Nasser Saber

Zur Veranschaulichung werden folgende vereinfachende Modellannahmen getroffen:

Für den herrschenden Zinssatz als risikolose alternative Verzinsung wird ein Wert von null angenommen. Ein Wertgegenstand (Basiswert, Underlying) habe den Ausgangspreis von 50 Euro. Es wird angenommen, dass dieser Preis bis zu einem bestimmten Termin sich

• entweder auf 60 Euro erhöht

• oder auf 40 Euro vermindert.

Bei einem einfachen Termingeschäft würde im ersten Fall Short an Long 10 Euro bezahlen, im zweiten Fall Long an Short 10 Euro. Das Geschäft ist fair, weil beide Seiten die gleichen Gewinn- und Verlustchancen haben unter der Annahme, dass man über die Eintrittswahrscheinlichkeiten der beiden Fälle nichts weiß oder dass sie gleich 0,5 gesetzt werden können.

Bei einer Call-Option erwirbt Long das Recht, die aus einem Termingeschäft folgende Zahlungverpflichtung von 10 Euro, sollte der Preis auf 40 Euro fallen, nicht zu erfüllen („right to default“).

Wie hoch ist der Kaufpreis für die Call-Option, damit dieses neue Geschäft von beiden Seiten als fair akzeptiert werden kann?

Antwort: Der Preis der Call-Option ist 5 Euro. Genau lautet die Berechnungsformel nach Nasser Saber^[1] für dieses Zahlenbeispiel:

C (Wert der Call Option) =
(60 Euro – 50 Euro)/(60 Euro – 40 Euro) mal (50 Euro – 40 Euro) = 5 Euro

Long zahlt zu Beginn an Short 5 Euro. Steigt der Preis des Basiswerts auf 60 Euro, kassiert er 10 Euro, abzüglich der für den Call gezahlten 5 Euro verbleiben ihm 5 Euro Gewinn. Sinkt der Preis auf 40 Euro, muss er gemäß Call-Option an Short nichts bezahlen, es bleibt bei einem Verlust von 5 Euro für den gekauften Call.

Umgekehrt hat Short im ersten Fall einen Verlust von 5 Euro. 5 Euro hat Short für den Verkauf der Call-Option an Long erhalten, 10 Euro muss er ihm wegen des gestiegenen Preises von 50 Euro auf 60 Euro bezahlen. Im zweiten Fall hat Short einen Gewinn von 5 Euro, die er für den Verkauf der Call-Option erhalten hat.

Im Endergebnis kann man dieses Optionsgeschäft als ein „verkürztes“ Termingeschäft auffassen. Der ursprüngliche Gewinn- oder Verlustbetrag hat sich von 10 Euro auf 5 Euro vermindert. Allerdings musste Long 5 Euro für die Call-Option zu Beginn auslegen. In dieser Deutung sind Optionsgeschäfte „Termingeschäfte des kleinen Mannes“ oder „an option is a poor man’s forward“.^[2]

Außerdem hat in diesem verkürzten Termingeschäft Long seinen möglichen Verlust von 5 Euro schon im Voraus bezahlt. Tritt für ihn der Verlustfall ein, der Preis sinkt, hat er keine weiteren Zahlungsverpflichtungen mehr, weil er schon bezahlt hat. Im Gewinnfall bekommt er den vorausbezahlten Betrag ersetzt und darüber hinaus den anfallenden Gewinn von 5 Euro. Saber sieht so Optionsgeschäfte als eine Möglichkeit breitere Massen, die früher mangels Kreditwürdigkeit von spekulativen Geschäften ausgeschlossen waren, Finanzgeschäften zuzuführen, indem diese eben ihren jeweils möglichen Verlust im Voraus bezahlen.^[3]

Verallgemeinert man die Modellannahmen, indem nicht nur zwei mögliche Preisveränderungen als möglich angesehen werden, sondern die Preise sich beliebig nach oben oder unten verändern können, dann ergeben sich für den Käufer und Verkäufer der Option jeweils entgegengesetzte Gewinn- und Verlustbereiche. Long, hier der Käufer der Option, macht einen Gewinn, wenn der Preis stärker als um um 5 Euro steigt oder fällt. Im ersten Fall erhält er mehr als ihn die Option gekostet hat (Optionspreis war 5 Euro). Im zweiten Fall gewinnt er, weil er eine Zahlungsverpflichtung von über 5 Euro dank seines durch den Optionskauf erworbenes Recht auf Nichterfüllung dieser Verpflichtung nicht nachkommen muss.

Steigt oder sinkt der Preis um weniger als 5 Euro, macht Long, hier als Käufer der Option, Verlust. Im ersten Fall gewinnt er durch den Preisanstieg weniger als ihn die Option gekostet hat, im zweiten Fall hat er mit 5 Euro mehr für die Option bezahlt, als er an Short hätte zahlen müssen.

Saber^[4] sieht dies so, dass entgegen verbreitetem Verständnis der Optionskäufer der „Spekulant“ ist in dem Sinne, dass er von hohen Preisveränderungen profitiert, während der Optionsverkäufer gewinnt wenn sich wenig ändert. Letzterer vertritt also die „konservative“ Seite in diesem Geschäft.

Berechnung des Preises einer Call-Option nach Black-Scholes

Zu Beginn verkauft Short an Long eine Call-Option. Gleichzeitig als Risikoausgleich oder Hedging kauft er X Stück des Basiswertes. Der Wert der gekauften Basiswerte erscheint in der Bilanz auf der Aktivseite, während die Verpflichtung aus oder der Wert der verkauften Call-Option auf der Passivseite erscheint. Zu Beginn des Geschäftes beträgt also der Wert dieses Vermögens^[5]

in Euro: 50 X – C

wobei X Anzahl der gekauften Basiswerte und C der Wert der Call-Option ist.

Zum Termin verändert sich der Wert des Portfolios:

Wenn der Preis des Basiswertes auf 60 Euro steigt, annahmegemäß die eine Möglichkeit, dann beträgt der Wert des Portfolios:

in Euro: 60 X - 10

Die -10 Euro ergeben sich, weil in diesem Fall der Käufer der Call-Option vom Verkäufer 10 Euro einfordern kann, da der Preis des Basiswertes von 50 Euro auf 60 Euro gestiegen ist.

Wenn der Preis des Basiswertes auf 40 Euro sinkt, annahmegemäß die andere Möglichkeit, dann beträgt der Wert des Portfolios:

in Euro: 40 X

Die Call-Option hat in diesem Fall einen Wert von null. Wenn der Preis sinkt, hat der Käufer der Call-Option gegenüber dem Verkäufer keine Zahlungsverpflichtung.

X ist jetzt so zu bestimmen, dass sich ein risikoneutrales Portfolio ergibt, das heißt der Wert des Portfolios muss gleich bleiben, gleichgültig ob Fall eins oder Fall zwei eintritt:

In Euro: 60 X – 10 = 40 X

Daraus ergibt sich X = 0,5. In beiden Fällen ergibt sich dann ein Portfoliowert von 20 Euro.

Der Preis der Call-Option ist jetzt so zu bestimmen, dass sich auch für das Portfolio zu Beginn des Geschäftes ein Wert von 20 Euro ergibt, anderenfalls würde eine der beiden Parteien zu Lasten der anderen einen Gewinn machen, d.h. es ergäbe sich die Möglichkeit zu einem Arbitrage-Geschäft. Setzt man X = 0,5 in den Portfoliowert zu Beginn des Geschäftes ein, dann ergibt sich:

In Euro: 50 * 0,5 – C = 20

C = 5 Euro.

Auch nach der Black-Scholes-Methode ergibt sich also für die Call-Option ein Preis von 5 Euro, obwohl dem Black-Scholes-Modell, nach Saber, ein anderes Optionsverständnis zugrunde liegt.

Einzelnachweise

1. ↑ Saber 1999, S. 44ff.
2. ↑ Saber 1999, S. 32
3. ↑ Saber 2006, S. 18f.
4. ↑ 2006, S. 23f.
5. ↑ Darstellung nach Saber 1999, S. 28ff.

Literatur

• John C. Hull: Optionen, Futures und andere Derivate. 6. Aufl., Pearson Studium, München 2006.
• Bloss, Michael; Ernst, Dietmar; Häcker Joachim (2008): Derivatives - An authoritative guide to derivatives for financial intermediaries and investors Oldenbourg Verlag München ISBN 978-3-486-58632-9

Weblinks

• Einsteigerkurs Optionsscheine
• Aktuelle Studien zur Bewertung von Aktienoptionen gemäß IFRS 2