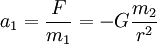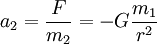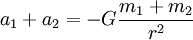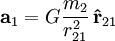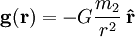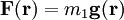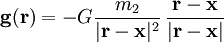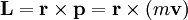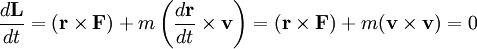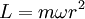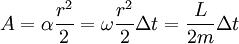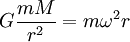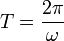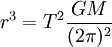- Gravitationsbeschleunigung
-
Das newtonsche Gravitationsgesetz wurde von Isaac Newton 1686 erstmals in seinem Werk Philosophiae Naturalis Principia Mathematica formuliert. Es besagt:
- Jede Masse, genauer jeder Massenpunkt, zieht jeden anderen Massenpunkt mittels einer Kraft an, die entlang der Verbindungslinie gerichtet ist. Der Betrag dieser Gravitationskraft ist proportional zum Produkt der beiden Massen und umgekehrt proportional zum Quadrat des Abstandes der beiden Massen. Damit ergibt sich die Kraft als:
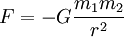
Dabei ist
- F die Kraft zwischen den Massenpunkten,
- m1 die Masse des ersten Massenpunktes,
- m2 die Masse des zweiten Massenpunktes,
- r der Abstand zwischen den Massenpunkten,
- G die Gravitationskonstante.
Das negative Vorzeichen der Kraft bringt hier zum Ausdruck, dass sie immer anziehend wirkt. Diese Vorzeichenkonvention wird hier übernommen, um Konsistenz mit dem Coulombgesetz zu wahren, wo sich Ladungen gleicher Vorzeichen abstoßen und Ladungen verschiedener Vorzeichen anziehen.
In SI-Einheiten wird F in Newton, m1 und m2 in Kilogramm und r in Meter gemessen. Die Gravitationskonstante ist eine Naturkonstante mit dem Wert
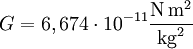 .
.Inhaltsverzeichnis
Grundlegende Eigenschaften
Gravitationsbeschleunigung
Wir nennen die Beschleunigung durch Gravitation, die die erste Punktmasse erfährt a1. Das zweite newtonsche Axiom besagt, dass Kraft und Beschleunigung proportional sind:
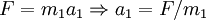 . Setzt man nun das Kraftgesetz der Gravitation ein, erhält man
. Setzt man nun das Kraftgesetz der Gravitation ein, erhält manDie Punktmasse m1 zieht die Masse m2 an und umgekehrt. Ihre Gesamtbeschleunigung aufeinander zu ist also die Summe der Einzelbeschleunigungen:
Falls nun eine der Massen viel kleiner ist als die andere, reicht es, die größere Masse zu berücksichtigen. So ist die Erde viel schwerer als ein Apfel, ein Mensch oder ein LKW, so dass es für alle diese Objekte reicht, die Masse der Erde in der Gleichung für die Beschleunigung einzusetzen. Alle drei Objekte werden also gleich beschleunigt und fallen gleich schnell. Wenn man jedoch ein Doppelsternsystem betrachtet, muss man beide Sternenmassen berücksichtigen, weil sie etwa gleich groß sind.
Falls r sich nur sehr geringfügig während der Bewegung eines Objektes verändert, erscheint die Gravitationsbeschleunigung konstant. Ein Beispiel dafür ist ein Gegenstand nahe der Erdoberfläche, der nur einige Meter tief fällt. Dies ist sehr wenig im Vergleich zum Erdradius r = 6370 km, so dass die Erdbeschleunigung als konstant angesehen werden kann. Bei einem sehr langen Objekt, z.B. einem Stab der Länge r/2 der hochkant steht, ist die Beschleunigung des unteren Endes sehr viel größer, als die des oberen Endes. Daher wird eine Kraft auf den Stab wirken, die versucht ihn auseinander zu ziehen. Man spricht dabei von einer Gezeitenkraft.
Vektorform
Das newtonsche Gravitationsgesetz lässt sich als Vektorgleichung formulieren, so dass nicht nur die Größe, sondern auch die Richtung der Kraft direkt aus dem Gesetz folgt. Vektoren werden hier durch Fettdruck des Größensymbols dargestellt.
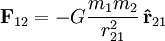 oder
oder 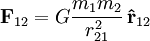
dabei ist
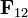 die Kraft auf Objekt 2 von Objekt 1
die Kraft auf Objekt 2 von Objekt 1- G die Gravitationskonstante
- m1 die Masse von Objekt 1 und m2 die Masse von Objekt 2
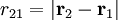 der Abstand zwischen Objekt 1 und Objekt 2
der Abstand zwischen Objekt 1 und Objekt 2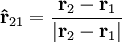 der Einheitsvektor von Objekt 1 zu Objekt 2
der Einheitsvektor von Objekt 1 zu Objekt 2
Man sieht, dass die Vektorform der oben gegebenen Form weitgehend gleicht, mit dem Unterschied, dass die Kraft nun eine Vektorgröße ist, also eine Richtung hat. Diese Richtung zeigt von Objekt 2 zu Objekt 1, wie man an der rechten Seite der Gleichung ablesen kann. Man kann sich auch leicht klar machen, dass
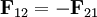 gilt, also auf das andere Objekt eine Kraft in entgegengesetzter Richtung wirkt. Die Objekte ziehen sich also an, da die Kräfte aufeinander zeigen.
gilt, also auf das andere Objekt eine Kraft in entgegengesetzter Richtung wirkt. Die Objekte ziehen sich also an, da die Kräfte aufeinander zeigen.Die Vektorform der Gravitationsbeschleunigung gleicht ebenso weitgehend der obigen Betragformel:
Ausgedehnte Körper
Reale Körper sind keine Punktmassen, sondern haben eine räumliche Ausdehnung. In diesem Fall nimmt man an, dass der Körper sich in kleinere Teile zerlegen lässt, die sich wieder als Punktmassen auffassen lassen und bildet dann die Summe über alle Teilkräfte. Im Grenzwert unendlich kleiner Teile, aus denen der Körper besteht muss man die Kraft in Vektorform über die Ausdehnung der beiden Körper integrieren.
Auf diese Weise kann gezeigt werden, dass ein Objekt mit sphärisch symmetrischer Massenverteilung sich von außen betrachtet verhält wie eine Punktmasse im Schwerpunkt des Körpers sich verhalten würde. Newton hat dieses Theorem in Philosophiae Naturalis Principia Mathematica gezeigt. Für nicht sphärisch symmetrische Körper ist das im allgemeinen nicht wahr.
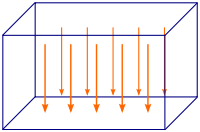
Gravitationsfeld
Das Gravitationsfeld ist ein Vektorfeld, das für alle Punkte im Raum die Gravitationskraft pro Masseneinheit angibt, die auf ein Objekt wirken würde. Es entspricht damit der Gravitationsbeschleunigung in jedem Punkt und ist eine Verallgemeinerung der Vektorform des Kraftgesetzes, die besonders dann interessant ist, wenn mehr als zwei Objekte betrachtet werden (wie z.B. bei einer Rakete zwischen Erde und Mond).
Um das Feld einer Punktmasse m2 zu beschreiben, wählt man zunächst zur Vereinfachung ein Koordinatensystem mit der Punktmasse im Ursprung. Dann kann man jeden Punkt mit einem Ortsvektor
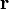 bezeichnen, wobei
bezeichnen, wobei 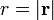 der Abstand des Punktes vom Ursprung ist. Das Feld
der Abstand des Punktes vom Ursprung ist. Das Feld 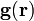 ist dann
ist dannMan erkennt, dass der Feldvektor auf den Ursprung zeigt, denn er zeigt am Punkt
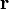 in die Richtung von
in die Richtung von 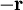 . Die Kraft auf eine Punktmasse m1 in diesem Feld ist dann
. Die Kraft auf eine Punktmasse m1 in diesem Feld ist dannWenn man das Feld mehrerer Punktmassen berechnen will, berechnet man wie oben die Felder aller Punktmassen und addiert sie. Man kann dann nicht mehr alle diese Punktmassen in den Ursprung des Koordinatensystems legen, daher wird die Formel für das Feld etwas komplizierter. Für eine Punktmasse am Ort
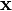 lautet sie:
lautet sie:Es wird also überall in der Formel der Verbindungsvektor vom Ursprung nach
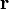 durch den Verbindungsvektor von
durch den Verbindungsvektor von 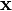 nach
nach 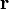 ersetzt. Die Kraft auf eine Punktmasse m ergibt sich dann wie oben indem man m mit dem Gesamtfeld der Punktmassen multipliziert.
ersetzt. Die Kraft auf eine Punktmasse m ergibt sich dann wie oben indem man m mit dem Gesamtfeld der Punktmassen multipliziert.Keplersche Gesetze
Die newtonsche Gravitationstheorie liefert eine Erklärung für die drei keplerschen Gesetze, die von Johannes Kepler 1609 bzw. 1619 veröffentlicht wurden. Das newtonsche Gravitationsgesetz muss in Verbindung mit der newtonschen Mechanik diese empirisch gefundenen Gesetzmäßigkeiten reproduzieren, um nicht im Widerspruch mit der Beobachtung zu sein. Die Tatsache, dass die Theorie die keplerschen Gesetze ebenso wie die Erdgravitation erklärt, kann als Beleg gesehen werden, dass sie in sehr guter Näherung die Gravitation beschreibt.
Im Folgenden wird ein Zweilkörperproblem betrachtet, wobei die Masse des schwereren Körpers M sehr viel größer sein soll, als die Masse des leichteren Körpers m. Dann kann man annehmen, dass der schwerere Körper ruht und die Kraftwirkung des leichteren Körpers auf ihn vernachlässigen.
Der Ellipsensatz
Das als Ellipsensatz bekannte erste keplersche Gesetz lässt sich auf verschiedene Weise aus dem newtonschen Gravitationsgesetz herleiten. Mit Hilfe der Bewegungsgleichungen ist der Beweis recht kurz aber auch mathematisch recht anspruchsvoll. Es ist auch möglich, den Beweis geometrisch mit einem Geschwindigkeitsvektordiagramm, dem sogenannten Hodograph, zu führen. Dieser Beweis ist mathematisch sehr viel einfacher aber dafür auch sehr viel aufwändiger.
Der Flächensatz
Der Flächensatz folgt aus der Drehimpulserhaltung. Der Drehimpulsvektor
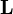 ist definiert als
ist definiert alsWobei
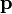 der Impuls und
der Impuls und 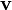 die Geschwindigkeit ist. Um zu zeigen, dass der Drehimpuls immer gleich bleibt, zeigt man, dass die Ableitung nach der Zeit verschwindet
die Geschwindigkeit ist. Um zu zeigen, dass der Drehimpuls immer gleich bleibt, zeigt man, dass die Ableitung nach der Zeit verschwindetdenn die Kraft zeigt immer in derselben Richtung wie
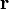 und
und 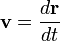 ist die Definition der Geschwindigkeit.
ist die Definition der Geschwindigkeit.Mit der Winkelgeschwindigkeit ω lässt sich der Betrag des Drehimpulses auf einer Kreisbahn schreiben als
Der Flächeninhalt des Kreissegments mit dem Innenwinkel α in Radiant beträgt
Der Flächeninhalt hängt also nur von der Länge des Zeitintervalls ab. Ein sehr kleines Stück einer Ellipse kann wie ein sehr kleines Stück eines Kreises behandelt werden, da sich auf einem sehr kleinen Stück der Abstand vom Schwerpunkt der Ellipse kaum ändert. Das bedeutet, die hergeleitete Formel für den Flächeninhalt der vom Fahrstrahl überstrichenen Fläche gilt bei sehr kleinen Zeitintervallen auch für Ellipsen. Für diese kleinen Zeitintervalle gilt der Flächensatz also.
Um das nun auf größere Zeitintervalle zu erweitern, muss man die Summe über die kleinen Zeitintervalle bilden. Genauer gesagt bildet man das Integral über unendlich kleine Zeitintervalle. Damit ist bewiesen, dass die Fläche, die der Fahrstrahl in einem bestimmten Zeitintervall überstreicht immer dieselbe ist.
Drittes keplersches Gesetz
Das dritte keplersche Gesetz ist für eine allgemeine elliptische Bahn eines Körpers sehr aufwändig zu beweisen. Daher wird es an dieser Stelle nur für eine Kreisbahn bewiesen. Auf einer Kreisbahn ändert sich der Abstand des Körpers von der Kreismitte nicht. Daher muss an jedem Punkt der Bahn die Gravitationskraft, die ihn zur Zentralmasse zieht genauso groß sein, wie die Zentrifugalkraft
Die Umlaufzeit T auf einer Kreisbahn hängt vom Kehrwert der konstanten Winkelgeschwindigkeit ab
Damit ergibt sich aus dem Kräftegleichgewicht
Also ist das Verhältnis r3 / T2 eine Konstante, die nicht von der Masse m des Objektes auf der Kreisbahn abhängt. Es ist für alle Planeten in demselben Sternensystem gleich.
Für allgemeine elliptische Bahnen wird die Rolle des Bahnradius von der großen Halbachse der Ellipse übernommen.
Grenzen der Theorie
Obwohl es für praktische Zwecke hinreichend genau ist, ist das newtonsche Gravitationsgesetz nur eine Näherung für schwache Gravitationsfelder. Für starke Felder verwendet man die genauere Beschreibung mittels der allgemeinen Relativitätstheorie, aus welcher die Poisson Gleichung der klassischen Gravitationstheorie und damit auch das newtonsche Gravitationsgesetz direkt hergeleitet werden kann, wenn man nur annimmt, dass es sich bei der Gravitation um ein konservatives Feld handelt. Man bezeichnet das Gesetz daher heute oft als Grenzfall kleiner Felder. Die allgemeine Relativitätstheorie löst insbesondere auch die hier beschriebenen Probleme der newtonschen Gravitationstheorie.
Theoretische Grenzen
- Die newtonsche Theorie ist eine effektive Theorie, das bedeutet, sie gibt weder eine Ursache für die Gravitationskraft an, noch erklärt sie, wie das Feld über die Entfernung wirken kann. Diese geisterhafte Fernwirkung war auch für Newton unbefriedigend. Um diese Erklärungslücke zu schließen, wurde die sogenannte Le-Sage-Gravitation als Modell entwickelt, das sich jedoch nie wirklich durchsetzen konnte.
- Die newtonsche Theorie setzt voraus, dass sich die Gravitationswirkung unendlich schnell ausbreitet, damit die keplerschen Gesetze erfüllt sind. Dies führte sehr viel später zu Konflikten mit der speziellen Relativitätstheorie. Diese fordert nämlich, dass sich die Gravitation nur mit Lichtgeschwindigkeit ausbreitet.
- Die Äquivalenz von träger und schwerer Masse ist in der newtonschen Mechanik allgemein unerklärt.
Widersprüche zur Beobachtung
- Die newtonsche Theorie erklärt nicht vollständig die Periheldrehung der Planetenumlaufbahnen, besonders des Merkur. Bei diesem beträgt der Unterschied zwischen der nach der newtonschen Theorie berechneten und der beobachteten Periheldrehung 43 Bogensekunden pro Jahrhundert.
- Die vorhergesagte Lichtablenkung an Körpern mit großer Masse entspricht nur der Hälfte der tatsächlich beobachteten Lichtablenkung.
Wikimedia Foundation.