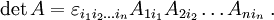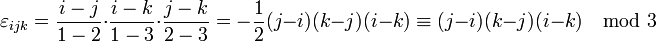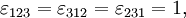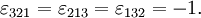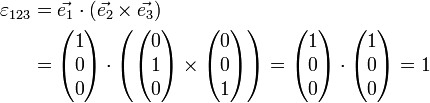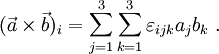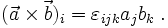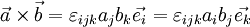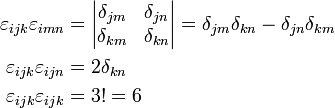Levi-Civita-Tensor

Das Levi-Civita-Symbol 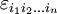$\varepsilon_{i_1i_2\dots i_n}$, auch Permutationssymbol, (ein wenig nachlässig) total antisymmetrischer Tensor oder Epsilon-Tensor genannt, ist ein Symbol, das in der Physik bei der Vektor- und Tensorrechnung nützlich ist. Das Symbol bezeichnet die Komponenten eines Tensors n-ter Stufe. Es ist benannt nach dem italienischen Mathematiker Tullio Levi-Cività (1873−1941). In der Mathematik spricht man stattdessen meist vom Vorzeichen der entsprechenden Permutation, siehe Alternierende Gruppe.

Die n Indizes i₁ bis i_n haben Werte von 1 bis n. Haben zwei Indizes denselben Wert, so ist 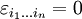$\varepsilon_{i_1\dots i_n}=0$. Sind die Werte der Indizes paarweise verschieden, so gibt das Symbol an, ob eine gerade (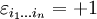$\varepsilon_{i_1\dots i_n}=+1$) oder eine ungerade (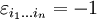$\varepsilon_{i_1\dots i_n}=-1$) Anzahl von Vertauschungen der Indizes nötig ist, um die Werte aufsteigend anzuordnen. Zum Beispiel ist 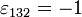$\varepsilon_{132}=-1$, da eine Vertauschung nötig ist, um 132 in die Reihenfolge 123 zu bringen.

Definition

Das Levi-Civita-Symbol in n Dimensionen hat n Indizes, die gewöhnlich von 1 bis n (für manche Anwendungen auch von 0 bis n-1) laufen. Es wird durch folgende Eigenschaften definiert:

• $\varepsilon_{12\dots n} = 1$.
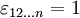• Unter Vertauschung zweier Indizes ändert es das Vorzeichen: $\varepsilon_{ij\dots u\dots v\dots} = -\varepsilon_{ij\dots v\dots u\dots}$.

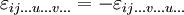Aus der zweiten Eigenschaft folgt sofort: Falls zwei Indizes gleich sind, ist der Wert null: $\varepsilon_{ij\dots u\dots u\dots} = 0$.

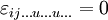Gleichwertig ist die Definition

$\varepsilon_{ijk\dots} = \begin{cases} +1, & \mbox{falls }(i,j,k,\dots) \mbox{ eine gerade Permutation von } (1,2,3,\dots) \mbox{ ist,} \\ -1, & \mbox{falls }(i,j,k,\dots) \mbox{ eine ungerade Permutation von } (1,2,3,\dots) \mbox{ ist,} \\ 0, & \mbox{wenn mindestens zwei Indizes gleich sind.} \end{cases}$

Eine alternative Definition verwendet eine Formel, welche auch für die Definition des Signums einer Permutation benutzt wird:

$\varepsilon_{i_1\dots i_n} = \prod_{1\le p<q\le n} \frac{i_p-i_q}{p-q}$.

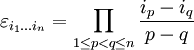Es bezeichne 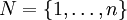$N=\{1,\dots,n\}$ die Menge der natürlichen Zahlen von 1 bis n. Man kann das Levi-Civita-Symbol als eine Abbildung 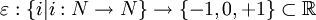$\varepsilon:\{i|i:N\rightarrow N\}\rightarrow\{-1,0,+1\}\subset\mathbb{R}$ auffassen mit 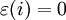$\varepsilon(i)=0$, falls i nicht bijektiv ist und 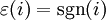$\varepsilon(i)=\sgn(i)$ sonst (also das Signum von i, falls i eine Permutation ist).

Zusammenhang mit der Determinante

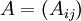Die Determinante einer $n \times n$-Matrix $A = \left(A_{ij}\right)$ kann mit dem Levi-Civita-Symbol und der Summenkonvention wie folgt geschrieben werden:

$\det A = \varepsilon_{i_1 i_2 \dots i_n} A_{1i_1} A_{2i_2} \dots A_{ni_n} \;.$

Allgemeiner gilt der Zusammenhang

$\varepsilon_{j_1 \dots j_n} A_{j_1i_1} \dots A_{j_ni_n} = \varepsilon_{i_1 \dots i_n} \det A$.

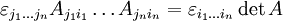Setzt man in diese Beziehung für A die Einheitsmatrix E_n ein, also für A_ij das Kronecker-Delta δ_ij, so erhält man wegen detE = 1 die folgende Darstellung des Levi-Civita-Symbols:

$\varepsilon_{i_1 \dots i_n} = \varepsilon_{j_1 \dots j_n} \delta_{j_1i_1} \dots \delta_{j_ni_n} = \begin{vmatrix} \delta_{1i_1} & \dots & \delta_{1i_n}\\ \vdots & & \vdots\\ \delta_{ni_1} & \dots & \delta_{ni_n} \end{vmatrix} = \det(e_{i_1}\dots e_{i_n})$.

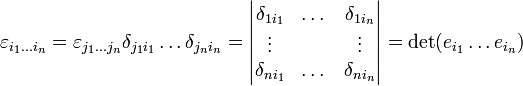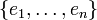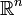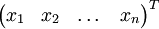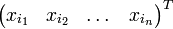Dabei sind die Spalten der Matrix die Einheitsvektoren aus der Standardbasis $\{e_1,\dots,e_n\}$ des $\mathbb R^n$. Diese Matrix ist also die Transponierte derjenigen Permutationsmatrix, welche den Vektor $\begin{pmatrix}x_1&x_2&\dots&x_n\end{pmatrix}^T$ auf $\begin{pmatrix}x_{i_1}&x_{i_2}&\dots&x_{i_n}\end{pmatrix}^T$ abbildet. Daraus erhält man mit Hilfe der Produktregel für Determinanten einen Ausdruck für das folgende Tensorprodukt:

$\varepsilon_{i_1 \dots i_n}\varepsilon_{j_1 \dots j_n} = \det \left((e_{i_1}\dots e_{i_n})^T\cdot(e_{j_1}\dots e_{j_n})\right) = \begin{vmatrix} \delta_{i_1j_1} & \dots & \delta_{i_1j_n}\\ \vdots & & \vdots\\ \delta_{i_nj_1} & \dots & \delta_{i_nj_n} \end{vmatrix}$.

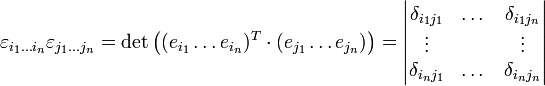Unter Verwendung des laplaceschen Entwicklungssatzes erhält man daraus die folgende Beziehung, wenn man über die jeweils ersten k Indizes beider Tensoren verjüngt:

$\varepsilon_{i_1 \dots i_k i_{k+1} \ldots i_n}\varepsilon_{i_1 \dots i_k j_{k+1} \ldots j_n} = k! \begin{vmatrix} \delta_{i_{k+1}j_{k+1}} & \dots & \delta_{i_{k+1}j_n}\\ \vdots & & \vdots\\ \delta_{i_nj_{k+1}} & \dots & \delta_{i_nj_n} \end{vmatrix}$.

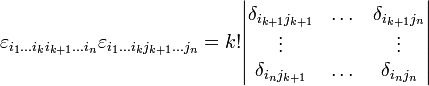Als Komponenten eines Tensors

Das Levi-Civita-Symbol bezeichnet die Komponenten eines vollständig antisymmetrischen Tensors, auch Volumenform genannt. Ein solcher Tensor ist nur bis auf einen skalaren Faktor bestimmt. Die Wahl des Vorfaktors fixiert die Volumeneinheit. Im euklidischen Raum steht das Levi-Civita-Symbol für die Komponenten des Standardvolumens in der Standardbasis 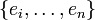$\{e_i,\dots,e_n\}$. Bezüglich einer anderen Basis e'_i = C_jie_j hat derselbe Tensor offenbar die Komponenten 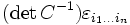$(\det C^{-1})\varepsilon_{i_1\dots i_n}$, wobei C = (C_ij) und C ^{− 1} die dazu inverse Matrix ist. Ist die Basis nicht orthonormal bezüglich des euklidischen Skalarprodukts, dann unterscheiden sich entsprechend ko- und kontravariante Komponenten des Tensors. Der Vorfaktor hängt von den Koordinaten ab, wenn krummlinige Koordinaten verwendet werden oder der zugrunde liegende Basisraum eine (orientierbare) Mannigfaltigkeit ist. Für eine semi-riemannsche Mannigfaltigkeit mit metrischem Tensor g und der zugehörigen riemannschen Volumenform (siehe Hodge-Stern-Operator) ist der Vorfaktor gegeben durch 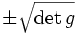$\pm\sqrt{\det g}$. Das Vorzeichen hängt von der gewählten Orientierung ab. Der Zusammenhang zwischen Levi-Civita-Symbol und Kronecker-Delta verallgemeinert sich zu

$(\det g)\varepsilon_{i_1 \dots i_n}\varepsilon_{j_1 \dots j_n}= \begin{vmatrix} g_{i_1j_1} & \dots & g_{i_1j_n}\\ \vdots & & \vdots\\ g_{i_nj_1} & \dots & g_{i_nj_n} \end{vmatrix}$.

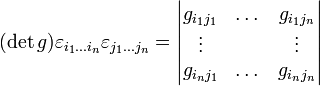Anwendungen

Vektorrechnung

Für den dreidimensionalen Fall ergibt sich

$\varepsilon_{ijk} = \frac{i-j}{1-2}\cdot\frac{i-k}{1-3}\cdot\frac{j-k}{2-3} = -\frac{1}{2}(j-i)(k-j)(i-k) \equiv (j-i)(k-j)(i-k) \mod 3$

wobei $i,j,k \in \lbrace1,2,3\rbrace$.

Levi-Civita-Symbol

Levi-Civita-Symbol

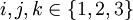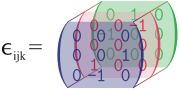
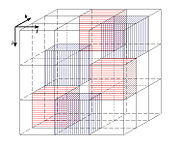
Lediglich sechs der 27 Komponenten von 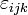$\varepsilon_{ijk}$ sind ungleich null:

$\varepsilon_{123} = \varepsilon_{312} = \varepsilon_{231} = 1 ,$

$\varepsilon_{321} = \varepsilon_{213} = \varepsilon_{132} = -1 .$

In diesem Beispiel erkennt man ferner eine Invarianz unter zyklischer Permutation der Indizes. Dies gilt allgemein nur dann, wenn n ungerade ist. Im anderen Fall geht eine zyklische Permutation mit einem Vorzeichenwechsel einher.

Das folgende Zahlenbeispiel demonstriert die Darstellung als Determinante, welche im dreidimensionalen Fall auch durch das Spatprodukt ausgedrückt werden kann:

$\begin{align} \varepsilon_{123} &= \vec{e_{1}} \cdot (\vec{e_{2}} \times \vec{e_{3}}) \\ &= \begin{pmatrix}1\\0\\0\end{pmatrix} \cdot \left(\begin{pmatrix}0\\1\\0\end{pmatrix} \times \begin{pmatrix}0\\0\\1\end{pmatrix}\right) = \begin{pmatrix}1\\0\\0\end{pmatrix} \cdot \begin{pmatrix}1\\0\\0\end{pmatrix} = 1 \end{align}$

Das Levi-Civita-Symbol mit drei Indizes erweist sich in der Vektorrechnung als nützlich, um die Komponenten des Kreuzproduktes zweier Vektoren zu schreiben. Es gilt

$(\vec{a} \times \vec{b})_i = \sum_{j=1}^3 \sum_{k=1}^3 \varepsilon_{ijk} a_j b_k \;.$

Bei solchen Rechnungen wird häufig die einsteinsche Summenkonvention angewandt, das heißt, man lässt die Summenzeichen weg und vereinbart, dass über in Produkten doppelt auftretende Indizes stets automatisch summiert wird:

$(\vec{a} \times \vec{b})_i = \varepsilon_{ijk} a_j b_k \;.$

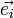Ist $\vec{e_i}$ der i-te Einheitsvektor, so kann diese Gleichung auch notiert werden als:

$\vec{a} \times \vec{b} = \varepsilon_{ijk} a_j b_k \vec{e_i} = \varepsilon_{ijk} a_i b_j \vec{e_k}$

Für das Spatprodukt gilt

$(\vec{a} \times \vec{b})\cdot\vec{c}=\varepsilon_{ijk} a_i b_j c_k$.

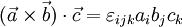In dieser Beziehung wird die Eigenschaft des Levi-Civita-Symbols als Komponenten einer Volumenform deutlich, denn das Spatprodukt ist gleich dem Volumen des von den drei Vektoren aufgespannten Spates.

Für den Zusammenhang zwischen dem Epsilon-Tensor und dem Kronecker-Delta erhält man die Beziehung

$\begin{align} \varepsilon_{ijk} \varepsilon_{lmn} &= \begin{vmatrix} \delta_{il} & \delta_{im} & \delta_{in} \\ \delta_{jl} & \delta_{jm} & \delta_{jn} \\ \delta_{kl} & \delta_{km} & \delta_{kn} \end{vmatrix}\\ &= \delta_{il} \delta_{jm} \delta_{kn} + \delta_{im} \delta_{jn} \delta_{kl} + \delta_{in} \delta_{jl} \delta_{km} -\delta_{im} \delta_{jl} \delta_{kn} - \delta_{il} \delta_{jn} \delta_{km} - \delta_{in} \delta_{jm} \delta_{kl} \end{align}$.

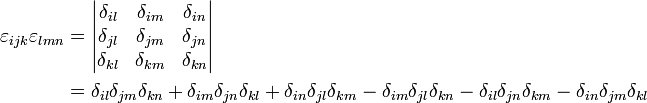Aus dieser folgt

$\begin{align} \varepsilon_{ijk} \varepsilon_{imn} &= \begin{vmatrix} \delta_{jm} & \delta_{jn} \\ \delta_{km} & \delta_{kn} \end{vmatrix} = \delta_{jm} \delta_{kn} - \delta_{jn} \delta_{km}\\ \varepsilon_{ijk} \varepsilon_{ijn} &= 2\delta_{kn}\\ \varepsilon_{ijk} \varepsilon_{ijk} &= 3! = 6 \end{align}$

(wiederum mit Summenkonvention). Diese Beziehungen sind hilfreich bei der Herleitung von Identitäten für das Kreuzprodukt.

Weiterhin ordnet der Epsilon-Tensor einem Vektor 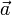$\vec{a}$ eine schiefsymmetrische Matrix A mit 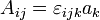$A_{ij}=\varepsilon_{ijk}a_k$ zu. Damit kann das Kreuzprodukt als Matrixprodukt 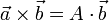$\vec{a}\times\vec{b}=A\cdot\vec{b}$ ausgedrückt werden. In der Mathematik wird diese Zuordnung als Hodge-*-Operator bezeichnet. Ein Beispiel ist die Zuordnung des magnetischen Feldvektors zu den entsprechenden Komponenten im elektromagnetischen Feldstärketensor. Solch eine Zuordnung ist auch für andere axiale Vektoren, etwa für den Drehimpulsvektor, üblich.

Relativitätstheorie

In der Relativitätstheorie muss zwischen ko- und kontravarianten Komponenten des Epsilon-Tensors unterschieden werden. Im Folgenden sei im vierdimensionalen Minkowski-Raum die Signatur des metrischen Tensors 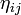$\,\eta_{ij}$ als (1,-1,-1,-1) festgelegt. Die Indizes sollen Werte von 0 bis 3 annehmen. Weiterhin sei für die vierfach kontravariante Komponente 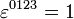$\varepsilon^{0123}=1$ festgelegt.^[1] Unterschiedliche Autoren verwenden verschiedene Konventionen für die Vorzeichen in Metrik und Epsilon-Tensor. Wie üblich werden Indizes mit dem metrischen Tensor bewegt. Dann erhält man zum Beispiel für die vierfach kovariante Komponente 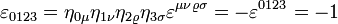$\varepsilon_{0123}=\eta_{0\mu}\eta_{1\nu}\eta_{2\varrho}\eta_{3\sigma}\varepsilon^{\mu\nu\varrho\sigma}=-\varepsilon^{0123}=-1$. Der Epsilon-Tensor kann verwendet werden, um den dualen elektromagnetischen Feldstärketensor 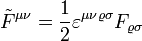$\tilde{F}^{\mu\nu}=\frac{1}{2}\varepsilon^{\mu\nu\varrho\sigma}F_{\varrho\sigma}$ zu definieren, mit dessen Hilfe sich wiederum die homogenen Maxwell-Gleichungen 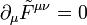$\partial_{\mu} \tilde{F}^{\mu\nu}=0$ kompakt notieren lassen.

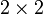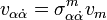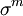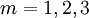Eine Anwendung des zweistufigen Epsilon-Tensors in der Relativitätstheorie ergibt sich, wenn man den Minkowski-Raum auf den Vektorraum der hermiteschen $2\times 2$-Matrizen abbildet: $v_{\alpha\dot\alpha}=\sigma^m_{\alpha\dot\alpha}v_m$. Dabei sind $\,\sigma^m$ für $\,m=1,2,3$ die Pauli-Matrizen und 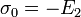$\,\sigma_0=-E_2$ die negative Einheitsmatrix. Entsprechend erfolgt dann die Zuordnung von Tensoren. Der metrische Tensor wird dabei auf das Produkt zweier Epsilon-Tensoren abgebildet: 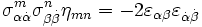$\sigma^m_{\alpha\dot\alpha}\sigma^n_{\beta\dot\beta}\eta_{mn}=-2\varepsilon_{\alpha\beta}\varepsilon_{\dot\alpha\dot\beta}$. In diesem Formalismus sind Objekte mit einem Index Spinoren 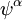$\,\psi^\alpha$, und der Epsilon-Tensor spielt bei der Umrechnung von ko- in kontravariante Komponenten die gleiche Rolle wie der metrische Tensor 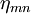$\,\eta_{mn}$ im gewöhnlichen Minkowski-Raum: 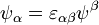$\psi_\alpha=\varepsilon_{\alpha\beta}\psi^\beta$. Dieser Formalismus ist unter dem Namen Van-der-Waerden-Notation bekannt. Für die Metrik wird üblicherweise die Signatur (-1,1,1,1) gewählt. Für den Epsilon-Tensor gilt hierbei die Festlegung 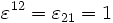$\varepsilon^{12}=\varepsilon_{21}=1$.^[2]

Quantenmechanik

In der Quantenmechanik wird das Levi-Civita-Symbol bei der Formulierung der Drehimpulsalgebra verwendet. In mathematischen Begriffen ausgedrückt stimmt das Symbol mit den Strukturkonstanten der Lie-Algebren 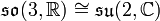$\mathfrak{so}(3,\mathbb R)\cong \mathfrak{su}(2,\mathbb C)$ überein. Das folgende Beispiel illustriert die Anwendung des Levi-Civita-Symbols in diesem Zusammenhang. Die Lie-Algebra 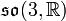$\mathfrak{so}(3,\mathbb R)$ kann als die Unteralgebra der schiefsymmetrischen Matrizen in 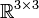$\mathbb R^{3\times 3}$, das heißt der reellen 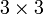$3\times 3$-Matrizen, dargestellt werden. Die Generatoren (eine Basis) von 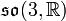$\mathfrak{so}(3,\mathbb R)$ ist gegeben durch die Matrizen 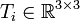$T_i\in\mathbb R^{3\times 3}$, i = 1,2,3, mit den Komponenten 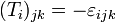$(T_i)_{jk}=-\varepsilon_{ijk}$. Die Kommutatoren der Generatoren lauten dann $[T_i,T_j]=\varepsilon_{ijk}T_k$.

Einzelnachweise

1. ↑ John David Jackson: Classical Electrodynamics. 3. Auflage. John Wiley & Sons, Inc., 1999, ISBN 0-471-30932-X. 
2. ↑ Julius Wess, Jonathan Bagger: Supersymmetry and Supergravity. Princeton University Press, 1983.