Phase-locked loop

Eine Phasenregelschleife, auch als englisch Phase-locked loop (PLL) bezeichnet, ist eine elektronische Schaltungsanordnung, die die Phasenlage und damit zusammenhängend die Frequenz eines veränderbaren Oszillators über einen geschlossenen Regelkreis so beeinflusst, dass eine möglichst kleine Phasenabweichung zwischen einem äußeren Referenzsignal und dem Oszillator- oder einem daraus abgeleiteten Signal erzielt wird.

Anwendungen findet die PLL in der Nachrichten-, Regel- und Messtechnik wie beispielsweise zur Realisierung von Filtern, zur Modulation und Demodulation, in digitalen Kommunikationssystemen zur Taktrückgewinnung und Synchronisation. Neben den in diesem Artikel behandelten elektronischen Schaltungen finden die zugrunde liegenden Prinzipien auch bei optischen Phasenregelschleifen Anwendung.

Geschichte

Erste Erwähnungen von analogen Phasenregelschleifen finden sich in britischen Arbeiten aus den frühen 1920er Jahren. ^[1] Die Schaltungen wurden mit Elektronenröhren realisiert und dienten in Folgejahren als Schaltungsteil in der damals aufkommenden Funktechnik und wurden unter anderem in Überlagerungsempfängern eingesetzt. Ziel war dabei die Minimierung der notwendigen Abstimmkreise und deren Stabilisierung im Betrieb. ^[2]

Wichtige Arbeiten zu den Grundlagen, ausgehend von der Theorie zu rückgekoppelten Verstärkern, lieferten in den 1930er Jahren die Arbeiten von Hendrik Wade Bode mit dem Bode-Diagramm und Harry Nyquist mit dem Stabilitätskriterium von Nyquist. ^[3][4] Darauf basierend wurden Phasenregelschleifen zunehmend auch in der Regelungstechnik zum Steuern von Aktoren wie Servomotoren verwendet. Bereits Anfang der 1950er Jahre wurden Phasenregelkreise zur Horizontalsynchronisation von Fernsehgeräten verwendet und es wurden erste Phasenregelschleifen zum Empfang der aufkommenden UKW-Radioprogramme im Rahmen der Frequenzdemodulation eingesetzt. ^[5] Es folgten Anwendungen im Bereich der Fernsehtechnik, insbesondere im Bereich des Farbfernsehens nach der NTSC-Fernsehnorm.

Mitte der 1960er Jahre setzte eine starke Verbreitung der PLL im Bereich der Konsumelektronik wie den Radio- und Fernsehgeräten ein. Die in der Anfangszeit diskret realisierten analogen Regelschleifen wurden zunehmend in integrierten Schaltungen (IC) zusammengefasst und von Firmen wie Signetics als fertige Bauelemente angeboten. ^[6] Daraus entwickelten sich im Elektroniksektor populäre Phasenregelschleifen, wie die von RCA entwickelte PLL-Schaltung mit der Bezeichnung CD4046. Dieses in CMOS-Technik realisierte IC fand große Verbreitung und wird auch noch im Jahr 2010 von verschiedenen Anbietern angeboten. ^[7]

Anfang der 1980er Jahre wurden die ersten digitalen Phasenregelschleifen entwickelt, die für den Bereich der digitalen Signalverarbeitung und der damit verknüpften Synchronisation von Sender- und Empfangsgeräten wesentlich sind. ^[8] Phasenregelschleifen wurden auch verschiedenartig im Aufbau modifiziert, wie es beispielsweise die Costas Loop zur Demodulation von digitalen Übertragungen darstellt.

Aufbau

Aufbau einer Phasenregelschleife

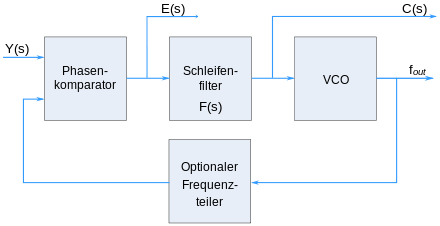
Die einfachste Form einer PLL besteht aus drei Komponenten, die in einem Regelkreis zusammengefasst sind und sich so gegenseitig beeinflussen:

1. Einem Phasendetektor. Dieser vergleicht an seinen beiden Eingängen die Phasenlage des Eingangssignals Y(s) mit der Phasenlage des gesteuerten Oszillators und liefert ein Ausgangssignal E(s) das in der Regelungstechnik auch als Fehlersignal (Error-Signal) bezeichnet wird. E(s) ist 0, wenn keine Phasenabweichung zwischen den beiden Eingängen vorliegt.
2. Einem Schleifenfilter mit der Übertragungsfunktion F(s), dem das Fehlersignal E(s) zugeführt wird und der an seinem Ausgang das Steuersignal oder Controll-Signal C(s) liefert. Der Schleifenfilter wird im Bereich der Regelungstechnik auch als Regler bezeichnet.
3. Einem steuerbaren Oszillator. In analogen Schaltungen meist in Form eines spannungsgesteuerten Oszillators (engl. Voltage Controlled Oscillator, VCO) realisiert, der beispielsweise durch eine Kapazitätsdiode in seiner Frequenz verändert werden kann. Bei digitalen PLLs sind numerisch gesteuerte Oszillatoren (engl. Numerically Controlled Oscillator, NCO) üblich. Dieser Oszillator kann über das Steuersignal C(s) in seiner Frequenz, die dem Phasendetektor entweder direkt oder über einen zusätzlichen Frequenzteiler zugeführt wird, in bestimmten Grenzen beeinflusst werden.

Im eingeschwungenen Zustand ergibt sich mit dieser Anordnung eine Nachführung der Oszillatorfrequenz und der Phase bezogen auf das zugeführte Referenzsignal. Je nach Anwendungsfall wird als Ausgang der PLL entweder das Fehlersignal E(s), das Steuersignal C(s) oder direkt die vom gesteuerten Oszillator erzeugte Schwingung betrachtet. Die drei Grundkomponenten werden je nach Anwendung verschieden ausgewählt und bestimmen das dynamische Betriebsverhalten des Regelkreises. Dabei versucht die Schleife, durch die negative Rückkopplung am Phasendetektor bestimmt, bei Veränderungen des Eingangssignals durch Nachjustieren des Oszillators das Fehlersignal möglichst klein und nahe dem Wert 0 zu halten.

Als Phasendetektor kommen bei analogen PLLs Analogmultiplizierer zur Anwendung, die im Bereich kleiner Fehlerwerte, bei E(s) nahe dem Wert 0, ein angenähert lineares Übertragungsverhalten aufweisen. Bei digitalen PLLs kommen XOR-Gatter oder sequentielle Logikschaltungen in Form von Flipflops zur Anwendung. Die Art des Phasendetektors bestimmt unter anderem das sogenannte Einrastverhalten der PLL.

Bei einem PLL-Sender, der FM-moduliert betrieben wird, muss noch berücksichtigt werden, dass der PLL die NF-Information (der Hub) zugeführt wird, damit diese die NF bei der Frequenzeinstellung berücksichtigt. Denn die FM-Modulation bewirkt eine Abweichung von der Sollfrequenz, so dass die PLL versucht, diese zu kompensieren. Durch das Zuführen der NF in die PLL wird diese gewollte Frequenzabweichung berücksichtigt und nicht kompensiert.

Ordnung einer PLL

Das lineare Schleifenfilter stellt einen Tiefpassfilter dar, dessen Übertragungsfunktion F(s) die dynamischen Eigenschaften der PLL wesentlich bestimmt. Das Schleifenfilter bestimmt, auf welche Art die Regelschleife auf Abweichungen reagiert. Die Übertragungsfunktion der offenen Schleife G(s) (engl. Open-Loop Transfer Function) besteht primär aus dem VCO und dem Schleifenfilter mit einem Verstärkungsfaktor k:

$G(s) = \frac{k \cdot F(s)}{s}$

Daraus kann die Übertragungsfunktion der geschlossenen Regelschleife H(s) (engl. Closed-Loop Transfer Function) ausgedrückt werden:

$H(s) = \frac{C(s)}{Y(s)} = \frac{G(s)}{1+G(s)}$

Daraus ergibt sich, dass die Ordnung H(s), und somit die Ordnung einer PLL, immer um eins höher als die Filterordnung des Schleifenfilters F(s) ist.

Bei einer PLL erster Ordnung wird als Besonderheit das Fehlersignal E(s) direkt dem gesteuerten Oszillator zugeführt, es gilt also E(s) = k · C(s) mit einem beliebigen konstanten Faktor k, der nur eine Verstärkung oder Dämpfung ausdrückt.

Bei einer PLL zweiter Ordnung weist der Schleifenfilter die allgemeine Übertragungsfunktion F(s) mit erster Ordnung auf:

$F(s) = \frac{a_0 + a_1 s}{b_0 + b_1 s}$

Und bei einer PLL dritter Ordnung:

$F(s) = \frac{a_0 + a_1 s + a_2 s^2}{b_0 + b_1 s + b_2 s^2}$

Je nach Wahl der Faktoren a_i, welche die Nullstellen, und b_i, welche die Polstellen bestimmen, werden die dynamischen Regeleigenschaften beschrieben. Bei Schleifen erster Ordnung ist ein konstanter Phasenfehler unvermeidbar, wenn die Eingangsfrequenz konstant neben der Eigenfrequenz des Oszillators liegt. Diese Regelabweichung kann nur über eine Erhöhung der Verstärkung k verringert werden, was zu Stabilitätsproblemen führen kann. Aus diesem Grund werden meistens Phasenregelschleifen zweiter Ordnung eingesetzt: Phasenfehler verschwinden asymptotisch, wenn die Frequenz am Eingang konstant bleibt. In Anlehnung an die Nomenklatur der Regelungstechnik werden die Parameter als Kreisfrequenz ω und Dämpfungsfaktor ζ bezeichnet. Bei PLLs dritter Ordnung verschwindet der Phasenfehler bei konstanter Chirprate.

In den unten angegeben Literaturquellen werden die verschiedenartige Typen von PLLs je nach Ordnung und innerhalb einer Ordnung in unterschiedlichen Typen klassifiziert und tabelliert.

Betriebsbereiche

Betriebsbereiche einer PLL

Die Abweichung der Eingangsfrequenz von der von dem steuerbaren Oszillator erzeugten Frequenz f_c beschreibt verschiedene Betriebsbereiche einer PLL, die für das Verhalten des Regelkreises wesentlich sind. Es wird dabei zwischen dem eingerasteten Betriebsbereich (engl. lock) der PLL, in dem stabiles Regelverhalten vorliegt, dem Einrastverhalten, wo die Regelschleife möglicherweise in den eingerasteten stabilen Betriebszustand übergeht, und dem nicht eingerasteten, freilaufenden Betriebszustand unterschieden.

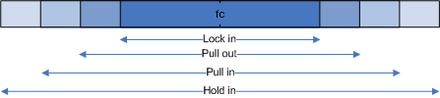
In nebenstehender Grafik sind die vier wesentlichen Betriebsbereiche angegeben, wobei die Abweichung der Eingangsfrequenz durch eine horizontale, symmetrische Abweichung von der zentrischen Lokalfrequenz f_c symbolisiert ist. Die genauen Grenzwerte hängen von der Art des Phasendetektors und des Schleifenfilters ab. Die Bereiche bedeuten:

1. Haltebereich (engl. Hold-In Range): Ist der größte Bereich, und die eingerastete Phasenregelschleife kann in diesem Bereich bei langsamer, nicht sprunghafter Änderung der Eingangsfrequenz der Eingangsfrequenz folgen. In diesem Fall liegt Regelverhalten vor.
2. Ziehbereich (engl. Pull-In Range): In diesem Bereich kann die PLL aus dem nicht eingerasteten Zustand nur mit Überspringen einer oder mehrerer Perioden in den eingerasteten Zustand überwechseln.
3. Ausrastbereich (engl. Pull-Out Range): Bei Anlegen eines Frequenzsprunges am Eingang an die eingerastete PLL kann sie in diesem Bereich ohne Überspringen einer Periode folgen. Auch in diesem Fall liegt Regelverhalten vor.
4. Fangbereich (engl. Lock-In Range): In diesem Bereich kann die PLL aus dem nicht eingerasteten Zustand direkt ohne Überspringen einer Periode in den eingerasteten Zustand überwechseln. Dieser Bereich ist der schmalste Bereich um die Oszillatorfrequenz.

Außerhalb des Haltebereichs liegt der nicht stabile freilaufende Betrieb vor, in dem weder ein Einrasten noch ein Halten eines zuvor erfolgten eingerasteten Betriebs möglich ist.

Digitale PLL

Phasenregelschleifen können im Rahmen der digitalen Signalverarbeitung auch als so genannte digitale PLL, abgekürzt DPLL, realisiert werden. Wesentlich dabei ist der Übergang von einem zeitkontinuierlichen System zu einem zeitdiskreten System, und an die Stelle der kontinuierlichen Laplace-Transformation zur Analyse tritt die diskrete Z-Transformation. Ein Vorteil von DPLLs besteht in der leichteren Reproduzierbarkeit.

Die Klassifizierung, ab welchem Umfang eine PLL als DPLL zu werten ist, ist in der Literatur nicht einheitlich. So kann nur ein Teil der PLL, beispielsweise nur das Schleifenfilter, als Digitalfilter realisiert werden. Typischerweise werden dabei die Entwurfsmethoden einer analogen PLL als Grundlage für die DPLL verwendet. Bei All-DPLLs wird die komplette Regelschleife inklusive NCO in digitalen Schaltungen aufgebaut.

So genannte Software-PLLs, die die Regelschleife als ein sequentielles Programm in einem digitalen Signalprozessor realisieren und meist bei niedrigen Frequenzen Anwendung finden, zählen ebenfalls zu dem Bereich der DPLLs. Bei Software-PLLs werden auch komplexe Phasendetektoren basierend auf der Hilbert-Transformation eingesetzt ^[9].

Anwendungen

PLLs umfassen ein breites Anwendungebiet und im folgenden Abschnitt sind beispielhaft einige Anwendungsbereiche beschrieben.

PLL als Nachlauffilter

Betrachtet man Frequenz und Phase des Referenzsignals als Eingangsgröße und das Oszillatorsignal als Ausgangsgröße, so verhält sich die beschriebene Anordnung ähnlich wie ein elektrischer Bandpass, wobei die Übertragungseigenschaften im Wesentlichen durch die Dimensionierung des Schleifenfilters festgelegt sind. Von besonderer Bedeutung bei der Anwendung der PLL als Bandpassfilter ist die Tatsache, dass dabei eine automatische Nachführung auf die Frequenz des Eingangssignals erfolgt. Gleichzeitig besteht bei dieser Anordnung die Möglichkeit, sehr kleine Nachführbandbreiten zu realisieren. Sie eignet sich daher in besonderem Maße zur Regeneration von verrauschten Signalen veränderlicher Frequenz.

PLL als Demodulator und Modulator

Mit dem Referenzsignal als Eingangsgröße und der Oszillator-Stellspannung als Ausgangsgröße eignet sich die PLL zur Anwendung als FM-Demodulator, solange die Modulationsfrequenz kleiner als die Nachführbandbreite bleibt. Die oben beschriebene Filterwirkung der PLL bleibt dabei erhalten, so dass auch noch extrem gestörte Signale demoduliert werden können.

Benutzt man die Ausgangsspannung des Phasendetektors als Ausgangssignal, dann lässt sich die PLL als Demodulator für phasenmodulierte Signale einsetzen. In diesem Fall muss die Nachführbandbreite kleiner als die niedrigste Modulationsfrequenz gewählt werden. PLL-basierte Phasendemodulatoren haben große Bedeutung in der Satellitenkommunikation erlangt.

Analog zu den Funktionen als Demodulator lässt sich die PLL als PM- und FM-Modulator einsetzen.

Frequenzsynthese

Prinzipschaltung eines PLL-Regelkreises

Ein Anwendungsbereich der PLL ist die Frequenzsynthese. Das nebenstehende Bild zeigt ein Blockschaltbild eines PLL-basierten Frequenzsynthesizers. Ein VCO (spannungsgesteuerter Oszillator) erzeugt das Ausgangssignal. Im Rückführungszweig der PLL ist ein Frequenzteiler vorgesehen, der die VCO-Frequenz vor dem Phasendetektor um einen einstellbaren Faktor herunterteilt. Das Referenzsignal der PLL wird typischerweise von einem genauen und stabilen Quarzoszillator bereitgestellt.

Im eingerasteten Zustand wird der VCO auf eine Frequenz geregelt, die um den Teilerfaktor größer ist als die Frequenz des Referenzsignals. Durch Ändern des Teilerfaktors lässt sich somit die Frequenz des VCOs auf genau ganzzahlige Vielfache der Referenzfrequenz einstellen. Ein wesentlicher Aspekt dabei ist, dass die Genauigkeit und Stabilität der festen Referenzfrequenz auch für die einstellbare Ausgangsfrequenz gelten.

Die beschriebene Anordnung lässt sich mit den heute verfügbaren Bauteilen zu geringen Kosten auf kleinstem Raum aufbauen und findet beispielsweise in Mobiltelefonen, Radios, Fernsehtunern und Funkgeräten massenhafte Anwendung. Typische Ausgangsfrequenzen liegen hier bei einigen hundert MHz, typische Referenzfrequenzen bei einigen 100 kHz. Frequenzteiler und Phasendetektor sind dabei meist in einer integrierten Schaltung realisiert, während der VCO und das Schleifenfilter oft diskret aufgebaut werden.

Wichtige Aspekte beim Entwurf eines PLL-Frequenzsynthesizers sind die spektrale Reinheit des Ausgangssignals, die Frequenzauflösung und die für eine Frequenzänderung benötigte Einrastzeit. Die spektrale Reinheit wird wesentlich von den Eigenschaften des VCOs, aber auch von den Rauscheigenschaften der übrigen Komponenten sowie von einem zweckmäßigen Aufbau (Abschirmung, Filterung) bestimmt. Die Frequenzauflösung ist beim oben beschriebenen System gleich groß wie die Referenzfrequenz. Die Einrastzeit hängt wesentlich von der Regelbandbreite ab, die aber nicht frei wählbar ist, sondern im Hinblick auf die benutzte Referenzfrequenz und die spektrale Reinheit des Ausgangssignals optimiert werden muss. Bei der Dimensionierung praktischer Systeme zeigt sich, dass eine hohe Frequenzauflösung im Widerspruch zu den Forderungen nach spektraler Reinheit und kurzer Einrastzeit steht.

Dieser Widerspruch ist durch Verwendung eines Frequenzteilers, der die VCO-Frequenz durch gebrochene Faktoren dividiert, auflösbar. Dazu muss der Teilfaktor zeitlich so variiert werden, dass sich im Mittel der gewünschte gebrochene Einstellwert ergibt^[10]. Am Ausgang des Phasendetektors entsteht dabei allerdings eine Störgröße, die mit geeigneten Gegenmaßnahmen kompensiert oder gefiltert werden muss (Delta-Sigma-Verfahren). Mit derart aufgebauten PLL-Synthesizern lassen sich beliebig feine Frequenzauflösungen bei gleichzeitig kürzesten Einrastzeiten und sehr hoher spektraler Reinheit realisieren.

Nachrichtentechnik, Messtechnik

PLLs eignen sich zur Erzeugung von stabilen Frequenzen bis in den GHz-Bereich (Funktechnik), Erzeugung von programmierbaren Frequenzen, Erzeugung von hochfrequenten Takten für Rechner sowie Synthesizer-Tuner, da mit Hilfe dieser Schaltungstechnik ein sehr exaktes Anwählen bzw. Ansteuern von Frequenzen möglich ist. Einerseits ist es möglich, mit einer festen Referenzfrequenz (Quarz-Oszillator) und einem variablem Feedback-Frequenzteiler eine präzise Ausgangsfrequenz zu erzeugen, was dem genannten Synthesizer-Prinzip entspricht. Andererseits kann man eine variable Frequenz mittels fest eingestelltem Feedback-Frequenzteiler mit einem fixen Faktor multiplizieren.

Neben der Anwendung als Frequenzerzeuger werden PLL-Schaltungen vor allem zur Demodulation von frequenz- oder phasenmodulierten Signalen, für Taktsynchronisation und Taktrückgewinnung eingesetzt.

Je nachdem, für welche Anwendung die PLL verwendet wird, unterscheidet sich auch, wo das Ausgangssignal abgegriffen wird. Die Frequenz des Oszillators wird z. B. bei Frequenz-Modulatoren verwendet, bei der Verwendung als Demodulator eines FM-Signals die Abstimmspannung des VCO.

Taktrückgewinnung

Einige Datenströme, besonders serielle, synchrone Datenströme (wie z. B. der Datenstrom des Magnetlesekopfes einer Festplatte), werden ohne getrenntes Taktsignal gesendet bzw. aus dem Speichermedium ausgelesen. Zur Taktrückgewinnung aus dem empfangenen Signal ist eine spezielle Leitungscodierung der zu übertragenden Nutzdaten notwendig, wie das beispielsweise der Manchester-Code darstellt.

Taktsynchronisation: Wenn parallel mit dem Datenstrom ein Takt gesendet wurde, muss dieser wiederaufbereitet werden, bevor er zur Verarbeitung der Daten genutzt werden kann. Das kostet jedoch einige Zeit, so dass Takt und Daten zunächst nicht mehr synchron zueinander sind. Die PLL sorgt dafür, dass der wiederaufbereitete Takt und der ursprüngliche Takt (und somit die Daten) wieder synchron sind.

Energietechnik

Eine PLL wird auch verwendet, um bei aktiven Systemen zur Leistungsfaktorkorrektur die Phasenlage aus den Außenleiterspannungen zu gewinnen. Mit Hilfe des Phasenwinkels kann eine Regelung vorgenommen werden, die dafür sorgt, dass die Außenleiterströme die gleiche Phasenlage wie die Phasenspannungen haben. Damit kann der Grundschwingungsleistungsfaktor auf Werte knapp unter 1 gebracht werden und das Leitungsnetz wird nicht mit Blindleistung belastet.

Erweiterungen

Eine Delay-Locked Loop (DLL) ist ähnlich wie eine PLL aufgebaut, weist aber keinen eigenen Oszillator auf und arbeitet statt dessen mit einem einstellbaren Laufzeitglied. Im Bereich der digitalen Frequenzsynthese spielt das Element der Direct Digital Synthesis (DDS) eine Rolle, die im Rahmen einer digitalen PLL als NCO Anwendung findet. Die Frequency Locked Loop (FLL) weist einen modifizierten Diskriminator auf und wird in der Literatur zur Gruppe der PLLs gezählt.

Literatur

• Donald R. Stephens: Phase-Locked Loops For Wireless Communications. 2. Auflage. Kluwer, 2002, ISBN 0-792-37602-1.

• Roland E. Best: Phase-Locked Loops. 6. Auflage. Mcgraw-Hill, 2007, ISBN 978-0-071-49375-8.

• Dieter Scherer, Bill Chan, Fred Ives, William Crilly, Donald Mathiesen: Low-Noise RF Signal Generator Design. Hewlett-Packard Journal, Feb. 1981.

• Bar-Giora Goldberg: Digital Frequency Synthesis Demystified - DDS and Fractional-N PLLs. LLH Technology Publishing., Eagle Rock 1999, ISBN 1-878707-47-7.

Einzelnachweise

1. ↑ J.H. Vincent: On Some Experiments in Which Two Neigboring Maintained Oscillatory Circuits Affect a Resonanting Circuit. Proceedings Royal Society, Vol. 32, Part 2, 1920, S. 84 bis 91.
2. ↑ H. de Bellescise: La réception Synchrone. Onde Electrique, 11. Ausgabe, 1932.
3. ↑ Hendrik Wade Bode: Relations Between Attenuation and Phase in Feedback Amplifier Design. Bell System Technical Journal, 19. Ausgabe, 1940, S. 421.
4. ↑ Harry Nyquist: Regeneration Theory. Bell System Technical Journal, 11. Ausgabe, 1932, S. 126.
5. ↑ J. Ruston: A Simple Crystal Discriminator for FM Oscillator Stabilization. Proceedings of the IRE, 39. Ausgabe, Nr. 7, 1951, S. 783 bis 788.
6. ↑ A.B. Grebene, H. R. Camenzind: Phase Locking As A New Approach For Tuned Integrated Circuits. ISSCC Digest of Technical Papers, 1969, S. 100 bis 101.
7. ↑ Datenblatt der PLL 4046 von NXP (Philips).
8. ↑ W.C. Lindsey, C.M. Chie: A Survey of Digital Phase-Locked Loops. Proceedings of the IEEE, 69. Ausgabe, Nr. 4, 1981, S. 410 bis 430.
9. ↑ J. Tierney, C.M. Rader: A Digital Frequency-Synthesizer. IEEE Transaction on Audio and Electromagnetics, Vol AU-19, 1971, S. 48 bis 57.
10. ↑ Technical Brief SWRA029 - Fractional/Integer-N PLL Basics von Texas Instruments.

Weblinks

 Commons: Phase-locked loops – Sammlung von Bildern, Videos und Audiodateien

• Alles zu PLL (Software, Berechnungen, Anwendungen, Definitionen,...)
• PLL-Tutorial
• Design Loop Filters For PLL Frequency Synthesizers
• Berechnung des Passive Loop Filters 3. Ordnung
• PLL-Frequenzsynthesizer mit digitalem Potentiometer