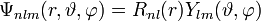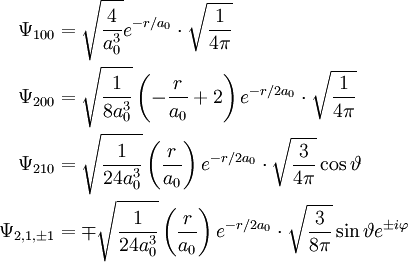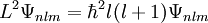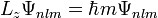Wasserstoffproblem

Ein Wasserstoffatom ist ein Atom des chemischen Elements Wasserstoff, der unter den auf der Erde herrschenden Bedingungen nur als zweiatomiges Wasserstoffmolekül vorkommt (gasförmiges H₂).

Das ¹H-Atom in der Isotopentabelle (Nuklidkarte)

Das Atom besteht aus einem einfach positiv geladenen Atomkern (mit einem Proton und null bis zwei Neutronen) und einem negativ geladenen Elektron. Elektron und Atomkern sind aufgrund ihrer entgegengesetzten elektrischen Ladung aneinander gebunden (coulombsches Gesetz).

Das Wasserstoffatom ist das am einfachsten aufgebaute aller Atome und bietet daher den Schlüssel zum Verständnis des Aufbaus und der Eigenschaften aller Atome. Es ist das einzige Atom, für das die quantenmechanische Schrödinger-Gleichung analytisch, d. h. in mathematisch geschlossener Form, gelöst werden kann. Die Spektrallinien des Wasserstoffatoms sind mit hoher Genauigkeit berechenbar, und können mit den gemessenen Werten verglichen werden, wie zum Beispiel das bekannteste Linienmultiplett, die Balmer-Serie.

Geschichte der Modellvorstellung des Wasserstoffatoms

Das 1913 entwickelte Bohrsche Atommodell stimmte in seiner Vorhersage der Spektrallinien gut mit experimentellen Beobachtungen überein, und zeigt auch eine hohe Übereinstimmung mit den 1925/26 berechneten quantenmechanischen Werten. Das quantenmechanische Modell lieferte zusätzlich die geometrische Struktur der Elektronenorbitale, und löste das Bohrsche Atommodell mit seinen Ad-hoc-Annahmen ab.

Verfeinerungen des quantenmechanischen Modells führten zu theoretischen Bestätigungen in der Detailstruktur der Spektrallinien des Wasserstoffatoms, das damit gleichzeitig zum Standardtest der Quantenmechanik avancierte.

Wichtige Phänomene, die anhand des Wasserstoffatoms erkannt oder verstanden wurden, sind unter anderem das Pauli-Prinzip und der Zeeman-Effekt.

Die am Wasserstoffatom abgeleiteten Prinzipien der Atomphysik bilden die Grundlage zur Beschreibung aller Atome. Allerdings kann das quantenmechanische Modell bei Atomen mit mehr als einem Elektron nur näherungsweise gelöst werden. Weiter haben Kenntnisse von Aufbau und Eigenschaften des Wasserstoffatoms zum Verständnis des Aufbaus chemischer Moleküle beigetragen.

Experimentelle Untersuchungen der Linienspektren

Termschema (Energieniveauschema) des Wasserstoffs

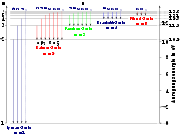
Seit 1885 werden die Absorptions- und Emissionsspektren des Wasserstoffatoms untersucht. Sie werden verursacht durch den Übergang des gebundenen Elektrons von einem höheren in ein niedrigeres Niveau (Emission) oder umgekehrt (Absorption). Dabei werden die möglichen Linien klassifiziert nach dem Grundniveau und benannt nach ihren jeweiligen Entdeckern. Mathematisch werden die Übergänge durch die Rydberg-Formel beschrieben.

Name der Serie	Grundniveau	Wellenlängenbereich	Entdeckungsjahr
Lyman-Serie	1	ultraviolett	1906
Balmer-Serie	2	sichtbar	1885
Paschen-Serie	3	infrarot	1908
Brackett-Serie	4	infrarot	1922
Pfund-Serie	5	infrarot	1924

Lösung der Schrödinger-Gleichung

Die dreidimensionale Schrödinger-Gleichung (eine partielle Differentialgleichung) kann aufgrund der Kugelsymmetrie der elektromagnetischen Wechselwirkung in drei unabhängige Gleichungen separiert werden. Jede der drei Einzelgleichungen kann mathematisch exakt gelöst werden.

Die wichtigste Gleichung ergibt die Energiezustände und Energiewerte des Elektrons im Wasserstoffatom; es ist üblich, die verschiedenen diskreten Energiewerte über die Hauptquantenzahl n als E_n zu bezeichnen. Der tiefste Energiezustand ist E₁, die weiteren Anregungszustände sind E₂ und E₃.

Die beiden anderen Gleichungen enthalten die Winkelabhängigkeit (Bahndrehimpulsquantenzahl, magnetische Quantenzahl).

Das Wasserstoffatom ist eines der wenigen quantenmechanischen Systeme, die sich exakt berechnen lassen. Die Lösung der Schrödinger-Gleichung für das Wasserstoffatom ist auch deshalb ein Standardverfahren der universitären Physik- und Chemieausbildung.

Mathematische Details

verschiedene Orbitale des Wasserstoffs

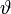Die Separation der Schrödinger-Gleichung führt zu drei Gleichungen, die von jeweils einer der drei Kugelkoordinaten $\,r$ (Abstand vom Mittelpunkt), $\vartheta$ (Breitenwinkel) und $\varphi$ (Längenwinkel) abhängen. Eine vollständige Lösung ergibt sich als das Produkt der Lösungen dieser 3 Gleichungen.

Jede Lösung 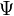$\,\Psi$ der Schrödinger-Gleichung für das Wasserstoffatom wird durch die drei Zahlen 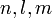$\, n, l, m$, Quantenzahlen genannt, gekennzeichnet. Dabei ist die Haupt- oder Energiequantenzahl 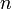$\,n$ eine beliebige positive Zahl, die Drehimpulsquantenzahl 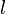$\,l$ nimmt für gegebenes 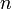$\,n$ die Werte von 0 bis n − 1 an, und die magnetische Quantenzahl 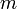$\,m$ läuft für gegebenes 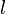$\,l$ von − l bis + l. Die Lösungsfunktion ist dann

$\Psi_{nlm}(r,\vartheta,\varphi) = R_{nl}(r) Y_{lm}(\vartheta, \varphi )$

mit

• $R_{nl}(r) = \sqrt {{\left(\frac{2}{n a_0}\right)}^3\frac{(n-l-1)!}{2n[(n+l)!]} } e^{- \rho / 2} \rho^{l} L_{n-l-1}^{2l+1}(\rho)$
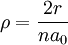• $\rho = {2r \over {n a_0}}$ (a₀ ist der Bohrsche Radius);
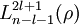• $L_{n-l-1}^{2l+1}(\rho)$ sind die zugeordneten Laguerre-Polynome;
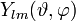• $Y_{lm}(\vartheta, \varphi )$ sind die Kugelflächenfunktionen.

Für die niedrigsten Orbitale ergibt sich damit:

$\begin{align} \Psi_{100} &= \sqrt{4 \over a_0^3} e^{-r/a_0} \cdot \sqrt{1 \over 4\pi}\\ \Psi_{200} &= \sqrt{1 \over 8 a_0^3} \left(-{r \over a_0} + 2\right)e^{-r/2a_0} \cdot \sqrt{1 \over 4\pi}\\ \Psi_{210} &= \sqrt{1 \over 24 a_0^3} \left({r \over a_0}\right)e^{-r/2a_0} \cdot \sqrt{3 \over 4\pi} \cos \vartheta\\ \Psi_{2,1,\pm 1} &= \mp \sqrt{1 \over 24 a_0^3} \left({r \over a_0}\right)e^{-r/2a_0} \cdot \sqrt{3 \over 8\pi} \sin \vartheta e^{\pm i \varphi}\\ \end{align}$

Die Energieeigenwerte sind

$H \Psi_{nlm} = E_n \Psi_{nlm} \,$

$E_n = -{{m_r c^2 Z^2 \alpha^2} \over {2 \cdot n^2}} = -{{m_r e^4 Z^2} \over {(4\pi\epsilon_0)^2 \hbar^2}} {{1} \over {2n^2}}= -{{e^2 Z^2} \over {4 \pi \epsilon_0 a_0}}\cdot {{1}\over {2 n^2}} \,$.

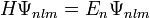
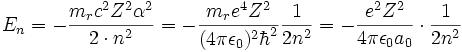Hierin ist α die Feinstrukturkonstante und m_r die reduzierte Masse des Systems aus Elektron und Proton. Die Drehimpuls- und magnetischen Eigenwerte sind durch

$L^2 \Psi_{nlm} = {\hbar}^2 l(l+1) \Psi_{nlm} \,$

und

$L_z \Psi_{nlm} = \hbar m \Psi_{nlm} \,$

gegeben.

Die Drehimpulsquantenzahl misst hierbei den Bahndrehimpuls des Elektrons, und die magnetische Quantenzahl seine Projektion auf eine beliebige Richtung, die im Allgemeinen als z bezeichnet wird (z steht dabei für die z-Achse). In dieser einfachsten Behandlung des Wasserstoffatoms sind die Energiewerte nur von der Hauptquantenzahl 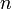$\,n$ abhängig. Alle Lösungen mit gleichem 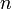$\,n$ besitzen hier die gleiche Energie. Man sagt daher, sie sind entartet bezüglich der Quantenzahlen 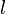$\,l$ und $\,m$. 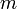Die Entartung bezüglich 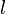$\,l$ ist dabei eine Besonderheit von (-a/r)-Potentialen.

Unter Berücksichtigung weiterer Effekte (Spin, Relativitätstheorie) ergibt sich eine zusätzliche Aufhebung der Energieentartung.

Alternativen zur Schrödinger-Theorie

In der heisenbergschen Matrizenmechanik hat Wolfgang Pauli für das Wasserstoffatom erstmals eine Lösung gefunden^[1], indem er die Rotationssymmetrie in vier Dimensionen [O(4)-Symmetrie] ausnutzte, die vom Drehimpuls und dem Laplace-Runge-Lenz-Vektor erzeugt wird. Durch Erweiterung der Symmetriegruppe O(4) zur Dynamischen Symmetriegruppe O(4,2) konnten nicht nur das Spektrum sondern auch die Dipol-Matrixelemente für alle atomaren Übergänge in einer irreduziblen Gruppendarstellung vereint werden^[2]

Im Jahre 1979 gelang auch eine Lösung für das Wasserstoffatom in Feynmans Pfadintegral-Zugang zur Quantenmechanik^[3][4]. Durch die hier entwickelte Lösungsmethode wurde der Anwendungsbereich der Feynmanschen Methode erheblich erweitert.

Weitere Entwicklung

Die Schrödinger-Gleichung gibt eine in erster Näherung ausgezeichnete Beschreibung des Wasserstoffatoms. Sie vernachlässigt allerdings eine Reihe von zweitrangigen Eigenschaften der beteiligten Elementarteilchnen, die experimentell nachweisbar sind. Durch Berücksichtigung dieser Eigenschaften im erweiterten quantenmechanischen Modell lassen sich jene Beobachtungen ebenfalls erklären.

Relativistische Effekte

Die Schrödinger-Gleichung ist eine nichtrelativistische Gleichung und verwendet den klassischen Ausdruck für die kinetische Energie, zur korrekten Beschreibung muss man deshalb eigentlich die Dirac-Gleichung verwenden. Beim Wasserstoffatom ist der Energieunterschied aber nicht sehr groß, daher kann man die Effekte störungstheoretisch im Rahmen der Schrödinger-Gleichung behandeln, um genauere Werte für die Energieeigenwerte zu erhalten.

Spin

Der Spin des Elektrons ist ebenfalls ein nicht klassischer Effekt, der sich exakt in der Dirac-Gleichung verstehen lässt.

Aufgrund seines Spins besitzt das Elektron ein magnetisches Moment, das mit anderen magnetischen Momenten und Magnetfeldern wechselwirken kann.

Die Wechselwirkung mit dem magnetischen Moment, welches das Elektron durch seine Bewegung um den Atomkern erzeugt, wird dabei als Spin-Bahn-Kopplung bezeichnet. Die Spin-Bahn-Kopplung und andere relativistische Effekte bewirken eine Aufspaltung der nicht-relativistisch entarteten Energieniveaus, die Feinstruktur des Wasserstoffatoms.

Berücksichtigt man noch die Wechselwirkung von Spin und Bahndrehimpuls mit dem Kernspin, ergibt sich eine noch feinere Aufspaltung, die sogenannte Hyperfeinstruktur.

In Anwesenheit von Magnetfeldern beobachtet man aufgrund des Spins des Elektrons den anomalen Zeeman-Effekt.

Quantenfeldtheoretische Effekte

Die Quantenmechanik ist eine Annäherung an die zugrundeliegende Quantenfeldtheorie, in der unter anderem Vakuumfluktuationen auftreten. Diese bedingen die Lamb-Verschiebung (engl. lamb shift) der Energiewerte, die erstmals im Lamb-Retherford-Experiment nachgewiesen wurde.

Diese Beobachtung führte zur Entwicklung der Quantenelektrodynamik, einer Quantenfeldtheorie, die mittels Näherungsrechnungen die bislang genaueste Beschreibung des Wasserstoffatoms gibt.

Einzelnachweise

1. ↑ W Pauli: Über das Wasserstoffspektrum vom Standpunkt der neuen Quantenmechanik. In: Zeitschrift für Physik. 36, 1926, S. 336–363. doi:10.1007/BF01450175
2. ↑ Kleinert H.: Group Dynamics of the Hydrogen Atom. In: Lectures in Theoretical Physics, edited by W.E. Brittin and A.O. Barut, Gordon and Breach, N.Y. 1968. 1968, S. 427-482
3. ↑ Duru I.H., Kleinert H.: Solution of the path integral for the H-atom. In: Physics Letters B. 84, Nr. 2, 1979, S. 185–188. doi:10.1016/0370-2693(79)90280-6
4. ↑ Duru I.H., Kleinert H.: Quantum Mechanics of H-Atom from Path Integrals. In: Fortschr. Phys. 30, Nr. 2, 1982, S. 401–435. doi:10.1002/prop.19820300802

Literatur

• David J. Griffiths: Introduction to Quantum Mechanics. 2. Auflage. Prentice Hall International, Upper Saddle River, NJ 2004, ISBN 0-13-111892-7 (Abschnitt 4.2 setzt sich genauer mit dem Wasserstoffatom auseinander). 
• B. H. Bransden, Charles J. Joachain: Physics of Atoms and Molecules. Longman, London 1982, ISBN 0-582-44401-2. 
• Hagen Kleinert: Path Integrals in Quantum Mechanics, Statistics, Polymer Physics, and Financial Markets: 5th Edition. 5. Auflage. World Scientific Publishing Co Pte Ltd, 2009, ISBN 981-427-355-4 (auch online lesbar). 

Weblinks

• Visualisierungen der Lösungen der Schrödinger-Gleichung
• Multimedia-Präsentationen zum Wasserstoff-Atom