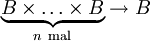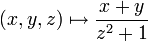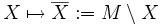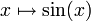- N-stellige Operation
-
In der Mathematik wird der Begriff Verknüpfung als Oberbegriff für Rechenoperationen (Addition, Subtraktion usw.) und Ähnliches verwendet.
Das Wort Verknüpfung wird auch benutzt, um die Hintereinanderausführung von Funktionen zu bezeichnen; siehe Komposition (Mathematik).
Inhaltsverzeichnis
Allgemeine Definition
Für eine natürliche Zahl n seien n Mengen
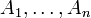 und eine weitere Menge B gegeben. Dann wird jede Abbildung des kartesischen Produkts
und eine weitere Menge B gegeben. Dann wird jede Abbildung des kartesischen Produkts  in B als n-stellige Verknüpfung bezeichnet. Eine solche Verknüpfung ordnet also jedem n-Tupel
in B als n-stellige Verknüpfung bezeichnet. Eine solche Verknüpfung ordnet also jedem n-Tupel 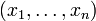 mit
mit 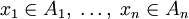 eindeutig ein Element der Menge B zu. Selbstverständlich können die Mengen
eindeutig ein Element der Menge B zu. Selbstverständlich können die Mengen 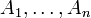 und B teilweise oder ganz übereinstimmen.
und B teilweise oder ganz übereinstimmen.Im Sonderfall, dass nur B vorkommt, also
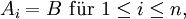 wird die Verknüpfung
wird die Verknüpfungn-stellige innere Verknüpfung auf B genannt. Kommt B wenigstens einmal unter den Ai vor, etwa
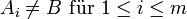 und
und 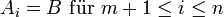
für ein m mit
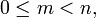 so heißt die Verknüpfung n-stellige äußere Verknüpfung auf B mit Operatorenbereich
so heißt die Verknüpfung n-stellige äußere Verknüpfung auf B mit Operatorenbereich 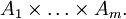 Die Elemente von
Die Elemente von 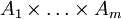 heißen dann Operatoren.
heißen dann Operatoren.Man sieht schon, dass man eine n-stellige innere Verknüpfung auf B auch als n-stellige äußere Verknüpfung auf B beispielsweise mit dem Operatorenbereich Bn − 1 betrachten kann.
Beispiele: Die durch
definierte Abbildung von
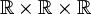 in
in  ist eine dreistellige Verknüpfung bzw. dreistellige innere Verknüpfung auf
ist eine dreistellige Verknüpfung bzw. dreistellige innere Verknüpfung auf 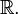
Ist f eine Abbildung von
 in
in  , so ist durch
, so ist durch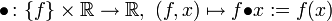
jedem Paar aus der Abbildung f und einem Element x aus R wird das Bild dieses Elementes unter der Abbildung zugeordnet
eine zweistellige äußere Verknüpfung auf
 mit Operatorenbereich {f} und dem einzigen Operator f gegeben.
mit Operatorenbereich {f} und dem einzigen Operator f gegeben.Jede n-stellige Verknüpfung kann als (n + 1)-stellige Relation aufgefasst werden.
Nullstellige Verknüpfungen
Eine nullstellige Verknüpfung von einer Menge A in eine Menge B ist eine Abbildung von A0 = {0} in B
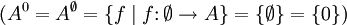 , nämlich
, nämlich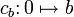 für ein
für ein 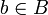 .
.
Da für jedes
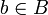 genau eine Abbildung cb existiert, gibt es eine Bijektion
genau eine Abbildung cb existiert, gibt es eine Bijektion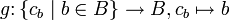 ,
,
so dass jedes cb nicht von b zu unterscheiden ist. Man kann daher cb auch als das Element
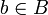 auffassen, also als eine Konstante in B.
auffassen, also als eine Konstante in B.Einstellige Verknüpfungen
Einstellige Verknüpfungen sind Abbildungen einer Menge A in eine Menge B.
Beispiele:
- Gegeben sei eine Menge M. Für jedes Element X der Potenzmenge P(M), also für jede Teilmenge X von M sei definiert:
- Die Sinusfunktion
ist eine Abbildung von
 in
in  und damit eine einstellige Verknüpfung.
und damit eine einstellige Verknüpfung.Zweistellige (binäre) Verknüpfungen
Hauptartikel: Zweistellige Verknüpfung
Besonders häufig wird der Begriff „Verknüpfung“ im Sinn einer zweistelligen Verknüpfung verwendet. Wichtige Spezialfälle sind innere und äußere Verknüpfungen. Zweistellige Verknüpfungen werden oft in Infixschreibweise notiert, also durch ein zwischen den beiden Operanden stehendes Symbol wie etwa ein Pluszeichen.
Drei- und mehrstellige Verknüpfungen
Eher selten spricht man von drei- und mehrstelligen Verknüpfungen. Ein Beispiel für eine dreistellige Verknüpfung ist die Abbildung, die je drei Vektoren aus dem
 ihr Spatprodukt (aus
ihr Spatprodukt (aus  ) zuordnet.
) zuordnet.Verknüpfungen in der Algebra
Verknüpfungen dienen in der Algebra dazu, algebraische Strukturen zu definieren. Die Verknüpfungen müssen dabei bestimmte Bedingungen (Axiome) erfüllen.
Zum Beispiel ist eine Halbgruppe eine Menge mit einer zweistelligen inneren Verknüpfung, die das Assoziativgesetz erfüllt. Die Forderung, dass das Ergebnis der Verknüpfung wieder Element der gegebenen Menge sein soll (Abgeschlossenheit), ist bereits in der Definition der inneren Verknüpfung enthalten.
Siehe auch
Wikimedia Foundation.