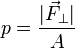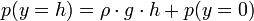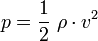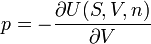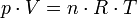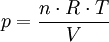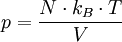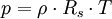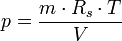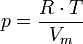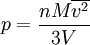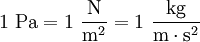InHg

Physikalische Größe
Name	Druck
Größenart	mechanische Spannung
Formelzeichen der Größe	p
Abgeleitet von	engl. pressure
Größen- und Einheiten- system Einheit Dimension SI Pascal (Pa), Bar (bar), N·m-2 M·L−1·T−2 Anglo- amerikanisch psi, in Hg M·L−1·T−2
Anmerkungen
spezielle Drücke werden durch Indizes bezeichnet. (z. B. pabs) veraltete Einheiten: at (ata, atü, atu), atm, Torr
Siehe auch: absoluter Druck, Luftdruck, Überdruck, atmosphärische Druckdifferenz

Der Druck ist eine intensive physikalische Zustandsgröße von thermodynamischen Systemen und zudem eine lineare Feldgröße.

Allgemein gilt, dass der Druck p (engl. pressure) den Betrag einer auf eine Fläche A (engl. area) normal stehenden Kraft F (engl. force) je Flächeninhalt von A darstellt:

$p = \frac {| \vec {F}_{\perp} |}{A} \,$

Die abgeleitete SI-Einheit des Drucks ist das Pascal Pa. Das Formelzeichen p darf hierbei nicht mit der Leistung P (von engl. power) beziehungsweise mit dem Impuls p verwechselt werden.

Das Konzept ist eine Vereinfachung des allgemeinen Spannungstensors. Die Druckspannung ist im Gegensatz zum Druck keine skalare Zustandsgröße. Die mechanische Spannung hat dieselbe physikalische Dimension wie der Druck, nämlich Kraft/Fläche. Der Druck stellt einen Spezialfall einer mechanischen Spannung dar.

Druck in strömenden Medien

statischer und dynamischer Druckanteil in einer Strömung

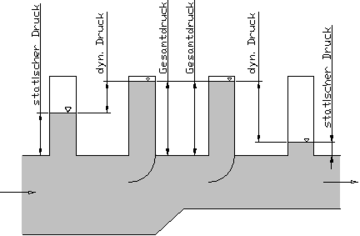
Der Druck in strömenden Medien setzt sich aus einem statischen und einem dynamischen Anteil zusammen. Während beide Teile von der Dichte abhängen, unterscheiden sie sich dadurch, dass der (hydro)statische Druck, für Fluide mit konstanter Dichte, linear mit der Höhe der Fluidsäule steigt. Zudem ist er von der Erdbeschleunigung, also der Gravitation, abhängig. Der dynamische Anteil hingegen wächst quadratisch mit der Strömungsgeschwindigkeit des Fluids. Das Bild zur Rechten verdeutlicht die Konstanz der Summe aus dynamischem und statischem Anteil in einer reibungsfreien Strömung. Dieses ist die Konsequenz aus der Energieerhaltung in der Strömung und für diesen Spezialfall als Gesetz von Bernoulli bekannt.

Hydrostatischer Druck

Der hydrostatische Druck übt auf jede Fläche, die mit dem Fluid in Verbindung steht, eine Kraft aus, die zur Größe der Fläche proportional wirkt – je größer die Fläche, desto größer wird also die darauf wirkende Kraft. Diese Form des Drucks ist somit eine spezielle Form der elastischen Spannungen, die idealen Flüssigkeiten und Gasen eigen ist: In der idealen (reibungsfreien) Flüssigkeit existieren ausschließlich Normalspannungen, eben jener hydrostatische Druck. Anders ist es in einer realen (reibungsbehafteten, viskosen) Flüssigkeit, denn hier können auch Tangential- oder Schubspannungen infolge der Reibungskräfte auftreten. Im Mohrschen Spannungskreis stellt sich der hydrostatische Druck daher als einfacher Punkt dar. Beispiele für einen hydrostatischen Druck sind der Wasserdruck und der Luftdruck.

Der hydrostatische Druck in einer Fluidsäule der Höhe h (auf einer y-Achse) und der Dichte ρ unter Wirkung der Erdbeschleunigung g, wobei mit p(y=0) der Druck auf der Oberfläche der Fluidsäule gemeint ist, ergibt sich als Sonderfall aus der hydrostatischen Grundgleichung zu

$p(y=h) = \rho \cdot g \cdot h + p(y=0) \,$

Hydrodynamischer Druck

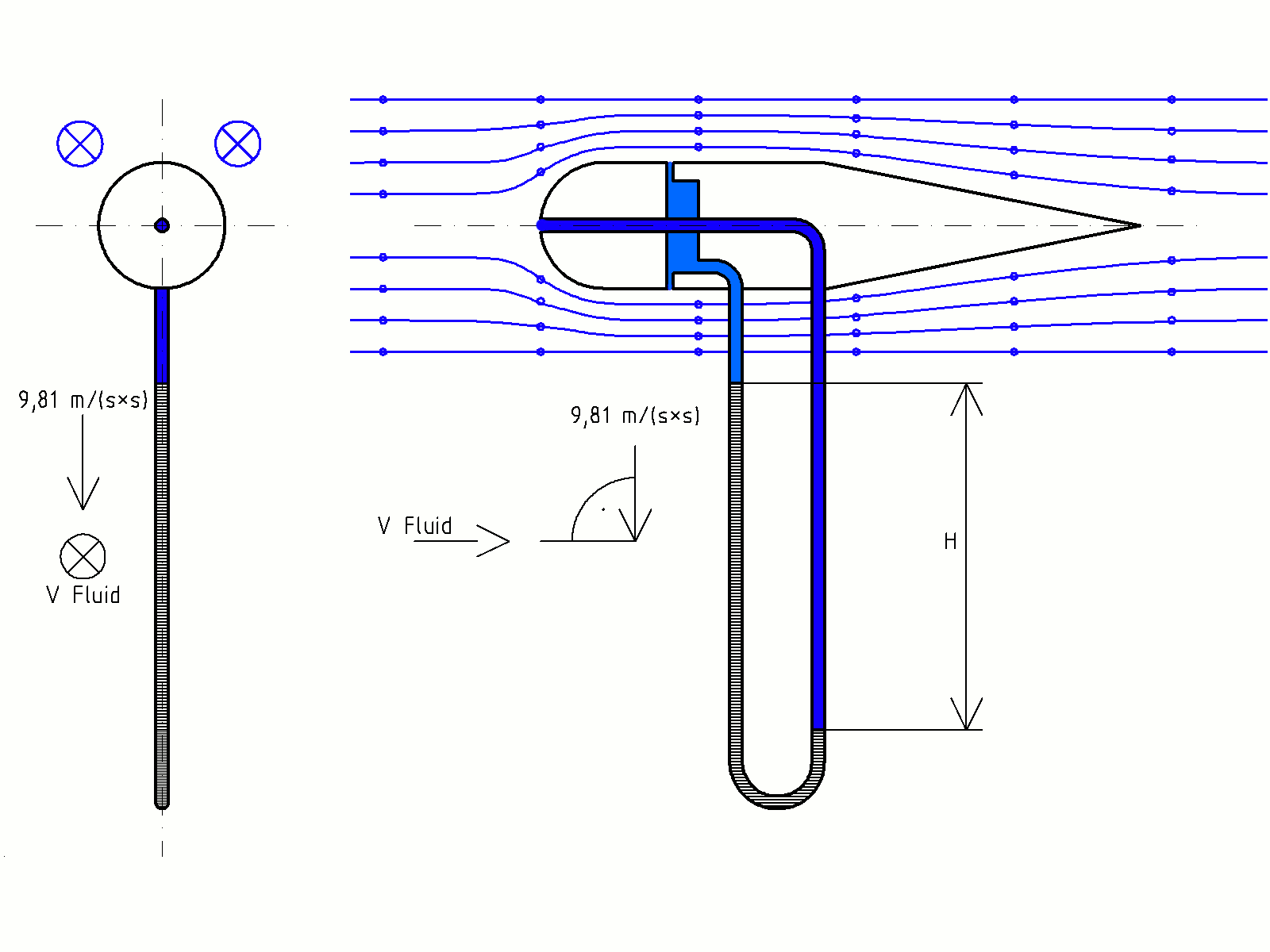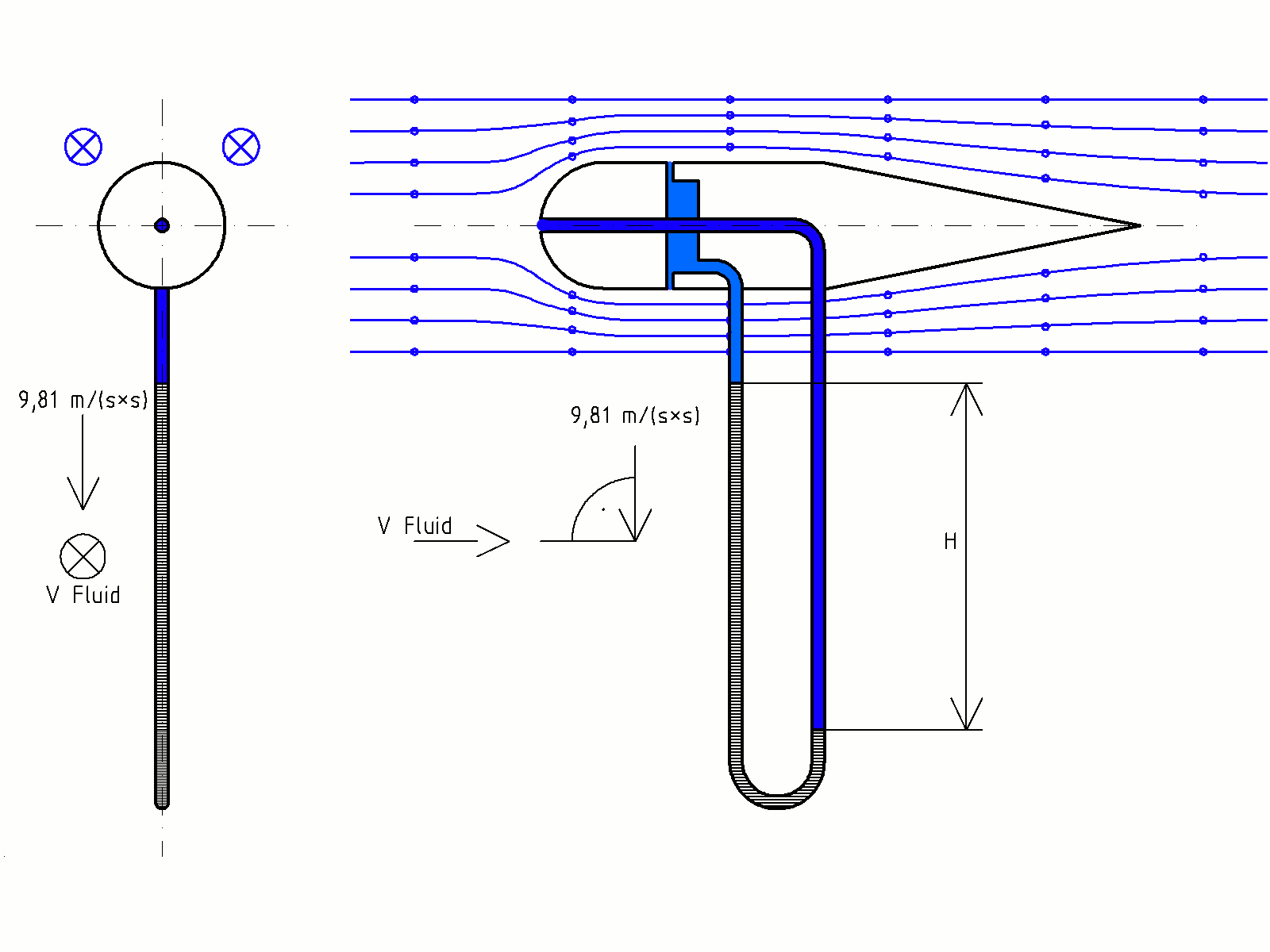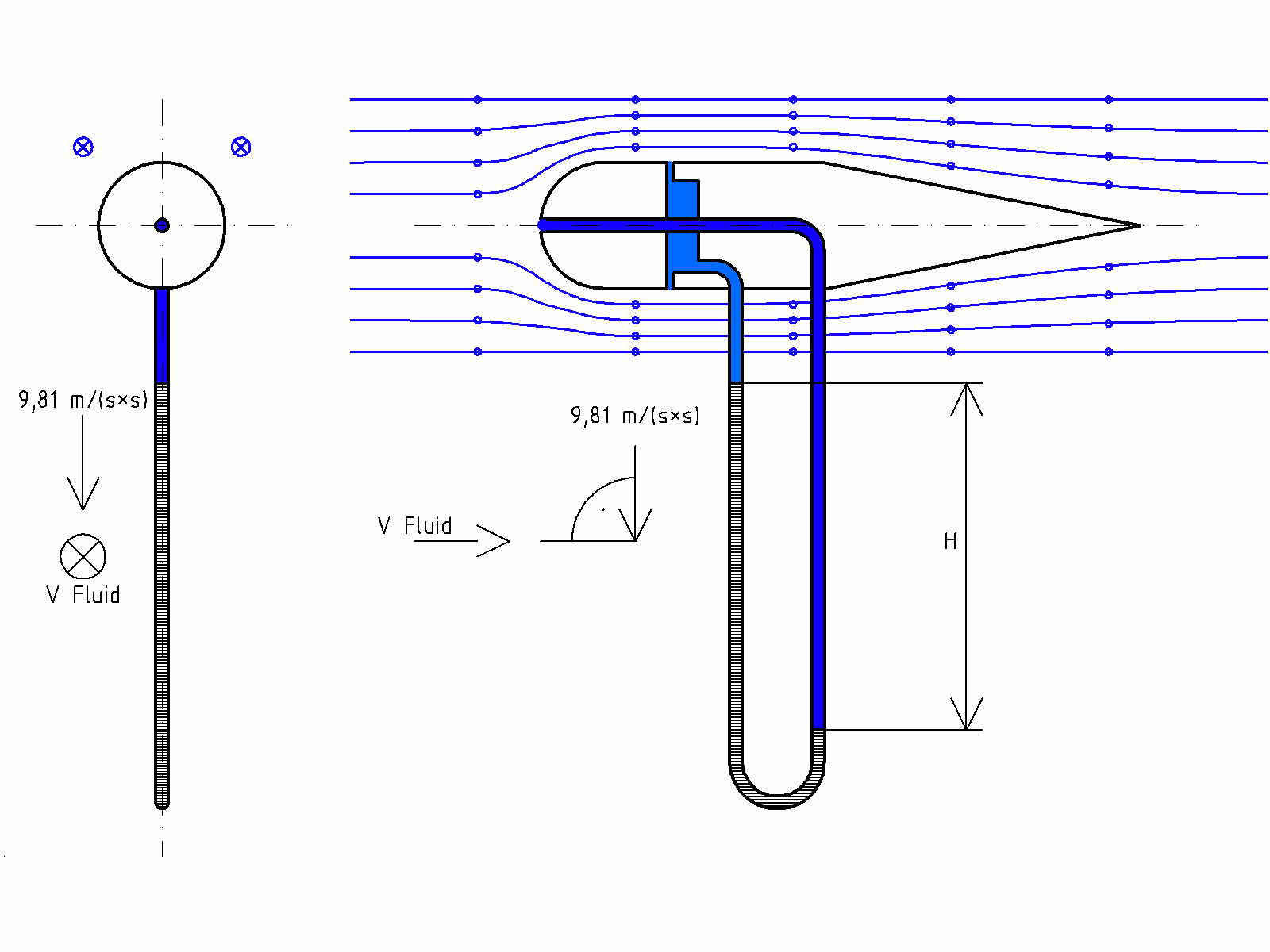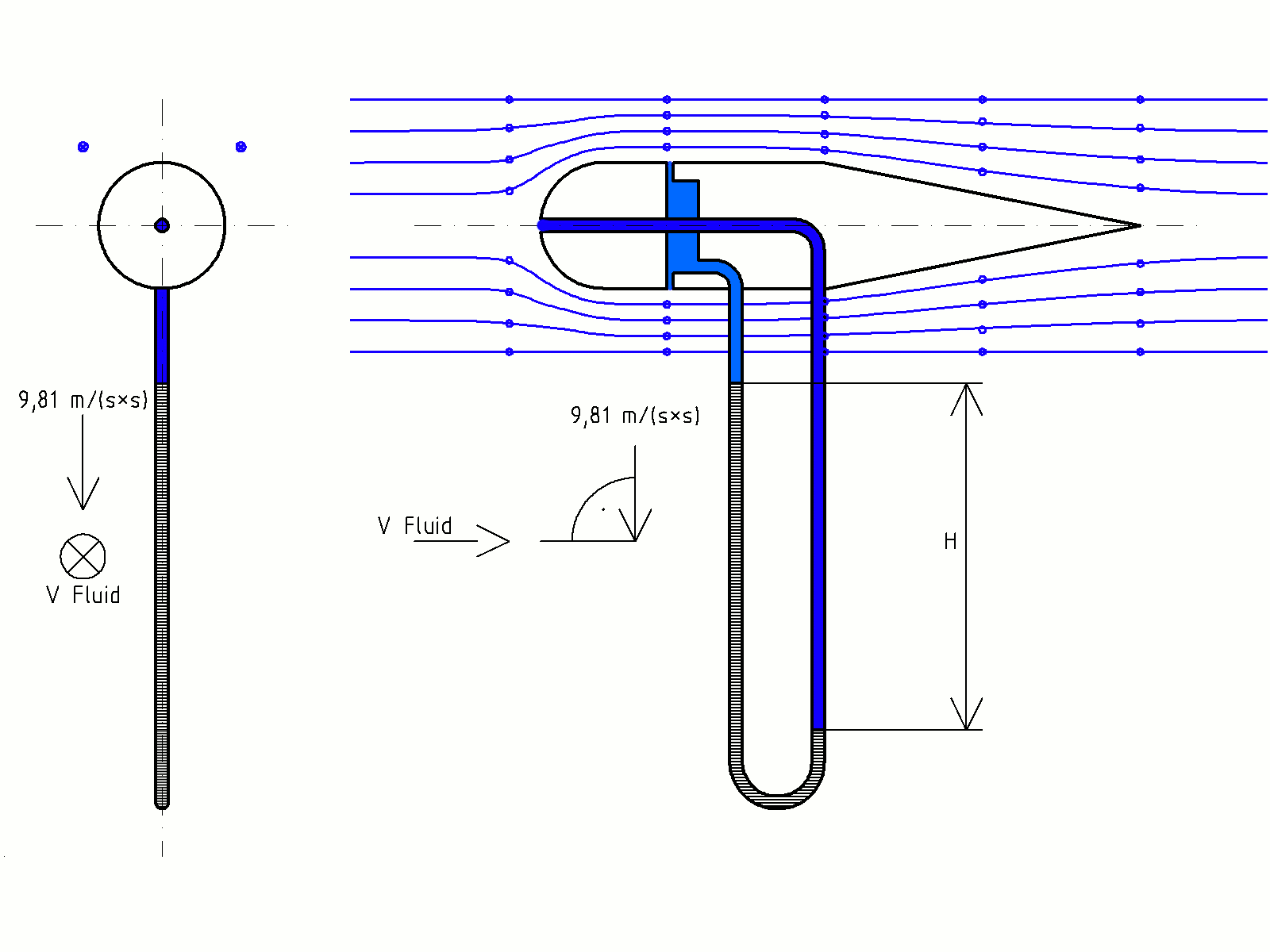prinzipielle Messeinrichtung für den Staudruck, Prinzip des Prandtl'schen Staurohrs, Differenzdruckmessung

Der hydrodynamische Druck, oder auch kürzer der dynamische Druck, resultiert aus der kinetischen Energie eines massebehafteten Körpers, der sich mit einer Geschwindigkeit fortbewegt, der sogenannten Fluidgeschwindigkeit. Er ist daher nach Daniel Bernoulli die Bezeichnung für die Verminderung des hydrostatischen Drucks, die aufgrund der Bewegung einer Flüssigkeit auftritt.

Die Geschwindigkeit kann von größeren zu kleineren Querschnitten aber nur zunehmen, wenn der Druck in den kleineren Querschnitten niedriger ist und umgekehrt. Durch die Strömung entsteht also in kleineren Querschnitten eine hydrodynamische Verringerung des Druckes, in größeren Querschnitten eine Erhöhung, infolge derer die in Ruhe befindlichen Druckverhältnisse – der hydrostatische Druck – verändert werden. Der hydrodynamische Druck ist dabei zwar nicht direkt messbar, wird aber zur Geschwindigkeitsmessung des Fluids verwendet. Es gilt:

$p = \frac{1}{2} \ \rho \cdot v^2 \,$

Gasdruck

Der Gasdruck entsteht als Summe aller durch ein Gas oder Gasgemisch wirkenden Kräfte auf eine Gefäßwand. Stößt ein Gasteilchen an eine Wand, so tauschen diese einen Impuls aus. Je wärmer das Gas ist, desto schneller sind die Teilchen und desto größer ist auch der Druck. Die Impulsübertragung hängt nämlich von der kinetischen Energie des Gasteilchens ab. Ebenfalls abhängig ist sie von der Richtung, mit der das Teilchen auf die Wand trifft. Für viele Teilchen addieren sich diese Impulsüberträge zu einer Gesamtkraft. Diese hängt hauptsächlich von der Anzahl der Teilchen ab, die pro Zeiteinheit auf die Wand treffen. Man erhält den Gasdruck auch durch eine Addition aller Partialdrücke der Komponenten des Gasgemisches. Hierbei stellen auch Dampfdruck und Sättigungsdampfdruck Sonderformen des Gasdrucks dar. Der Luftdruck ist ein Beispiel für einen Gasdruck.

Die kinetische Gastheorie liefert aus den genannten mechanischen und statistischen Überlegungen die Zustandsgleichung:

$p = -\frac{\partial U(S,V,n)}{\partial V} \,$

die sich für die Thermodynamik auch als Definition des Druckes als intensive Größe anbietet (siehe auch Fundamentalgleichung). Für ein ideales Gas führt dieses zur thermischen Zustandsgleichung:

$p \cdot V = n \cdot R \cdot T \,$

Aus ihr lassen sich verschiedene Formeln für den Gasdruck ableiten:

$p = \frac{n \cdot R \cdot T}{V} \,$

$p = \frac{N \cdot k_B \cdot T}{V} \,$

$p =\rho \cdot R_s \cdot T \,$

$p = \frac{m \cdot R_s \cdot T}{V} \qquad \,$

$p = \frac{R \cdot T}{V_m} \,$

Aus der kinetischen Gastheorie folgt:

$p = \frac{n M \overline{v^2}}{3 V} \,$

Hierbei stehen die einzelnen Formelzeichen für folgende Größen:

• T - Temperatur
• N - Teilchenanzahl
• n - Stoffmenge
• m - Gasmasse
• ρ - Dichte
• V - Volumen
• V_m - molares Volumen
• k_B - Boltzmannkonstante
• R - Universelle Gaskonstante
• R_s - spezifische Gaskonstante
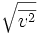• $\sqrt {\overline{v^2}}$ - quadratisch gemittelte Teilchengeschwindigkeit

Der gemittelte Impulsübertrag ist im Produkt aus Gaskonstante und Temperatur der Zustandsgleichung enthalten. Beide Begriffe können durch Kolbenprobeexperimente ineinander überführt werden. Der Gasdruck kann äquivalent zur obigen Definition auch als hydrostatischer Spannungstensor, wie er aus der Mechanik bekannt ist, verstanden werden.

Absoluter Druck

Der absolute Druck nimmt ab Vakuum kontinuierlich zu. Im Vakuum ist der Absolutdruck also 0.

Relativer Druck

Der relative Druck ist, wie der Name schon sagt, eine relative Druckbeziehung zwischen zwei Behältern. Z.B. ist der Druckunterschied zwischen dem Umgebungsdruck und dem Druck in einem Gefäß ein relativer Druck.

Einheiten

Die SI-Einheit des Druckes ist das Pascal mit dem Einheitenzeichen Pa. Ein Pascal entspricht einem Druck von einem Newton pro Quadratmeter:

$\mathrm{1 \ Pa = 1 \ \frac{N}{m^2} = 1 \ \frac{kg}{m \cdot s^2}} \,$

Für höhere Drücke wird auch gerne die SI-konforme Einheit Bar verwendet, 1 bar entspricht dabei 100.000 Pa = 1.000 hPa oder 100 kPa.

Im Ingenieurwesen wird für Druck ebenso wie für mechanische Spannung auch die Einheit N/mm² verwendet:

$\mathrm{1 \ \frac{N}{mm^2} = 1 \ MPa = 10 \ bar} \,$

Andere teilweise noch zu findende, aber nicht mehr zulässige Druckeinheiten sind:

• 1 Torr = 1 mm Hg = 1 mm Quecksilbersäule = ca. 133,3 Pa
• 1 Zoll Quecksilber (inch of mercury, inHg) = 3386,389 Pa bei 0 °C
• 1 Meter Wassersäule (mWS) = 0,1 at = 9,80665 kPa
• 1 Technische Atmosphäre (at) = 1 kp/cm². = ca. 98066,5 Pa
• 1 Physikalische Atmosphäre (atm) = 760 Torr = 101325 Pa = 1013,25 hPa = 101,325 kPa.
• 1 psi = 1 lb.p.sq.in. = 144 lb.p.sq.ft = 1/200 tn.sh.p.sq.in = 1/2240 tn.p.sq.in = 0,07030695796 kp/cm² = 6894,757293168 Pa

Druckeinheiten und Umrechnungsfaktoren

	Pascal (Pa)	Bar (bar)	Technische Atmosphäre (at)	Physikalische Atmosphäre (atm)	Torr (torr)	Pfund-Kraft pro Quadratzoll (psi)
	≡ 1 N/m²	≡ 1 Mdyn/cm²	≡ 1 kp/cm²	≡ pSTP	≡ 1 mmHg	≡ 1 lbf/in.²
1 Pa	1	1,0000 · 10−5	1,0197 · 10−5	9,8692 · 10−6	7,5006 · 10−3	1,4504 · 10−4
1 bar	1,0000 · 105	1	1,0197 · 100	9,8692 · 10−1	7,5006 · 102	1,4504 · 101
1 at	9,8067 · 104	9,8067 · 10−1	1	9,6784 · 10−1	7,3556 · 102	1,4223 · 101
1 atm	1,0133 · 105	1,0133 · 100	1,0332 · 100	1	7,6000 · 102	1,4696 · 101
1 torr	1,3332 · 102	1,3332 · 10−3	1,3595 · 10−3	1,3158 · 10−3	1	1,9337 · 10−2
1 psi	6,8948 · 103	6,8948 · 10−2	7,0307 · 10−2	6,8046 · 10−2	5,1715 · 101	1

Exponentialdarstellung auf vier Stellen gerundet.

Druckmessgeräte

Druckmessgeräte (Manometer) beruhen auf verschiedenen Messprinzipien:

• Zum Messen des Reifendrucks am Auto oder des Hauswasser- und Hausgasdrucks werden einfache Rohrfeder-Manometer oder Bourdonfeder-Manometer („Narrentröte“) verwendet. Diesen liegt das Prinzip eines eingerollten Schlauchs zu Grunde, der sich unter Druck aufrollt.
• Messgeräte für statische Drücke messen meist die Druckdifferenz anhand der Auslenkung einer mechanischen Trennung, indem der Druck mit einem Referenzdruck, etwa Vakuum verglichen wird. So messen etwa die Barometer und die Ringwaage, indem die Auslenkung direkt in eine Anzeige übersetzt wird, oder Differenzdrucksensoren, indem die Kraft der Auslenkung gemessen wird.
• Indirekte Druckmessung beruht auf Effekten der Teilchenzahldichte
• Messgeräte für Drücke in fliessenden Medien (Fluiden) nutzen die Eigenheiten der Bernoulli-Gleichungen, etwa das Staurohr (Pitotrohr) oder die Venturidüse
• Blutdruckmessgeräte messen indirekt, indem akustische Ereignisse beim Entspannen der vorher komprimierten Adern aufgefangen werden

Spezielle Drücke

• Luftdruck / Atmosphärischer Druck (Strömungswiderstand)
• Wasserdruck
• Turgor
• Schalldruck
• Staudruck
• Strahlungsdruck
• Nenndruck
• Gasbetriebsdruck
• Prüfdruck
• Berstdruck
• Osmotischer Druck
• Blutdruck
• Vakuum
• Gravitationsdruck
• Solardruck (Sonnenwind)
• Dampfdruck
• Öldruck
• Magnetischer Druck

Weblinks

• Druckeinführung
• Versuche und Aufgaben zum Druck
• Die angewendeten internationalen Druckeinheiten