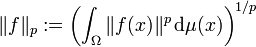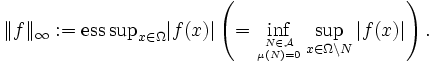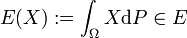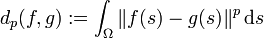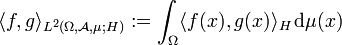- Lebesgue-Räume
-
In der Mathematik sind Lp-Räume spezielle Banachräume, die aus Räumen sogenannter „p-fach integrierbarer“ Funktionen gebildet werden. Das L in der Bezeichnung geht auf den französischen Mathematiker Henri Léon Lebesgue zurück, da diese Räume über das Lebesgue-Integral definiert werden. Manchmal werden sie daher auch als Lebesgue-Räume bezeichnet. Im Fall Banachraum-wertiger Funktionen (wie im Folgenden für allgemeines E dargestellt) bezeichnet man sie auch als Bochner-Lebesgue-Räume. Das p in der Bezeichnung ist ein reeller Parameter: Für jede Zahl
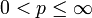 ist ein Lp-Raum definiert.
ist ein Lp-Raum definiert.Inhaltsverzeichnis
Definition
Funktionenraum mit Halbnorm
Sei
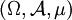 ein Maßraum, E ein Banachraum mit der Norm
ein Maßraum, E ein Banachraum mit der Norm  und
und 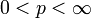 . Dann ist die Menge
. Dann ist die Menge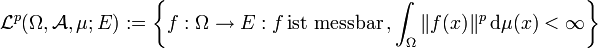 ,
,
wobei „messbar“ sich auf die borelsche σ-Algebra der Normtopologie von E bezieht, ein Vektorraum. Die Abbildung
ist eine Halbnorm auf
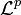 , wenn
, wenn 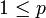 . Die Dreiecksungleichung für diese Halbnorm wird Minkowski-Ungleichung genannt und mit Hilfe der Hölder-Ungleichung bewiesen. Nach dem rieszschen Vollständigkeitssatz ist der Raum, versehen mit dieser Halbnorm, vollständig.
. Die Dreiecksungleichung für diese Halbnorm wird Minkowski-Ungleichung genannt und mit Hilfe der Hölder-Ungleichung bewiesen. Nach dem rieszschen Vollständigkeitssatz ist der Raum, versehen mit dieser Halbnorm, vollständig. ist genau dann eine Norm, wenn die einzige Nullmenge die leere Menge ist. Gibt es nämlich eine Nullmenge
ist genau dann eine Norm, wenn die einzige Nullmenge die leere Menge ist. Gibt es nämlich eine Nullmenge 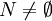 , so ist die charakteristische Funktion 1N ungleich der Nullfunktion, aber es gilt
, so ist die charakteristische Funktion 1N ungleich der Nullfunktion, aber es gilt 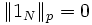 .
.Faktorraum mit Norm
Um im Fall der Halbnorm einen normierten Raum zu erhalten, definieren wir den Unterraum
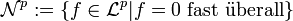 . Der Raum Lp ist dann definiert als der Faktorraum
. Der Raum Lp ist dann definiert als der Faktorraum 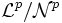 . Zwei Elemente von
. Zwei Elemente von ![[f], [g]\in L^p](/pictures/dewiki/53/5ad15b13551ea2bfd7dadbdbefbc675c.png) sind genau dann gleich, wenn f und g fast überall gleich sind.
sind genau dann gleich, wenn f und g fast überall gleich sind.Der Vektorraum Lp ist durch
![\|[f]\|_p:=\|f\|_p](/pictures/dewiki/49/1c9bf1d7b7f3fa97f169678cea7249e3.png) normiert. Die Normdefinition hängt nicht von dem Repräsentanten aus [f] ab, das heißt, für Funktionen
normiert. Die Normdefinition hängt nicht von dem Repräsentanten aus [f] ab, das heißt, für Funktionen ![f_1,f_2\in[f]](/pictures/dewiki/50/27e776235282590a09907dce8d13a949.png) in der gleichen Äquivalenzklasse gilt
in der gleichen Äquivalenzklasse gilt 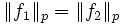 . Das begründet sich damit, dass das Lebesgue-Integral invariant gegenüber Änderungen des Integranden auf Nullmengen ist. Der normierte Vektorraum Lp ist vollständig und damit ein Banachraum.
. Das begründet sich damit, dass das Lebesgue-Integral invariant gegenüber Änderungen des Integranden auf Nullmengen ist. Der normierte Vektorraum Lp ist vollständig und damit ein Banachraum.Auch wenn man von sogenannten Lp-Funktionen spricht, handelt es sich dabei um die gesamte Äquivalenzklasse einer klassischen Funktion. Allerdings liegen im Falle des Lebesgue-Maßes auf dem
 zwei verschiedene stetige Funktionen nie in der gleichen Äquivalenzklasse, so dass der Lp-Begriff eine natürliche Erweiterung des Begriffs stetiger Funktionen darstellt.
zwei verschiedene stetige Funktionen nie in der gleichen Äquivalenzklasse, so dass der Lp-Begriff eine natürliche Erweiterung des Begriffs stetiger Funktionen darstellt.Sonderfall
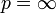
Auch für
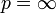 kann man einen Lp-Raum, den Raum der wesentlich beschränkten Funktionen, definieren. Hierfür gibt es verschiedene Möglichkeiten, die aber für σ-endliche Maßräume alle zusammenfallen. Am verbreitetsten ist:
kann man einen Lp-Raum, den Raum der wesentlich beschränkten Funktionen, definieren. Hierfür gibt es verschiedene Möglichkeiten, die aber für σ-endliche Maßräume alle zusammenfallen. Am verbreitetsten ist: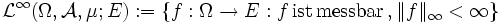 ;
;
dabei ist
Betrachten wir analog zu oben
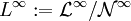 , erhalten wir wieder einen Banachraum.
, erhalten wir wieder einen Banachraum.Beispiele
- Ein sehr wichtiges Beispiel von Lp-Räumen ist durch einen Maßraum
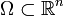 gegeben,
gegeben, 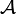 ist dann die borelsche σ-Algebra
ist dann die borelsche σ-Algebra 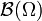 , und μ das Lebesgue-Maß λ. Darüber hinaus wird E oft als die Menge
, und μ das Lebesgue-Maß λ. Darüber hinaus wird E oft als die Menge  der reellen Zahlen gewählt. In diesem Zusammenhang wird die kürzere Notation
der reellen Zahlen gewählt. In diesem Zusammenhang wird die kürzere Notation 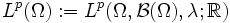 benutzt.
benutzt.
Einige Autoren schreiben den Parameter p unten statt oben: Lp statt Lp.
- In der Stochastik betrachtet man Lp-Räume, die mit einem Wahrscheinlichkeitsmaß P ausgestattet sind. Unter einer Zufallsvariable versteht man dann eine messbare Funktion
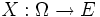 . Weiter ist der Erwartungswert als
. Weiter ist der Erwartungswert als
definiert. Zufallsvariablen, die L1-Funktionen sind, besitzen also einen endlichen Erwartungswert. Da das für praktische Anwendungen immer gefordert ist, sind Lp-Räume gerade in der Stochastik sehr wichtig.
- In einem weiteren wichtigen Fall sind Ω die natürlichen Zahlen und μ das normale Zählmaß. Hier ist der Lp-Raum der Raum aller Zahlenfolgen
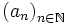 , für die die Reihe
, für die die Reihe 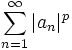 konvergiert. Diese Räume werden auch oft mit
konvergiert. Diese Räume werden auch oft mit 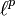 bezeichnet.
bezeichnet.
Wichtige Eigenschaften
- Alle Lp-Räume für
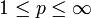 sind Banachräume.
sind Banachräume. - Ist μ ein endliches Maß, gilt also
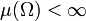 , so folgt beispielsweise aus der Ungleichung der verallgemeinerten Mittelwerte, dass
, so folgt beispielsweise aus der Ungleichung der verallgemeinerten Mittelwerte, dass 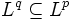 für
für 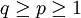 . Für allgemeine Maße gilt für
. Für allgemeine Maße gilt für 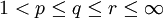 stets
stets 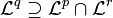 . Dies wird auch als "konvexe" oder "Hölder-Interpolation" bezeichnet.
. Dies wird auch als "konvexe" oder "Hölder-Interpolation" bezeichnet. - Für
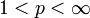 sind die Dualräume der Lp-Räume über reflexiven Banachräumen E wieder Lp-Räume. Konkret gilt:
sind die Dualräume der Lp-Räume über reflexiven Banachräumen E wieder Lp-Räume. Konkret gilt:
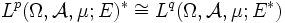 ,
,- worin q definiert ist über
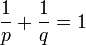 ; dabei ist der kanonische isometrische Isomorphismus gegeben durch
; dabei ist der kanonische isometrische Isomorphismus gegeben durch
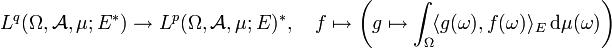 .
. - Dabei steht
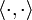 für die kanonische Bilinearform auf
für die kanonische Bilinearform auf 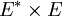 , nämlich
, nämlich 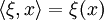
- Daraus folgt, dass für
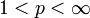 und reflexives E die Lp-Räume reflexiv sind.
und reflexives E die Lp-Räume reflexiv sind. - Für p = 1 und
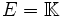 ist
ist 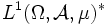 zu
zu 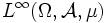 isomorph (der Isomorphismus analog zu oben), falls
isomorph (der Isomorphismus analog zu oben), falls  σ-endlich ist. Ist
σ-endlich ist. Ist  nicht σ-endlich, so lässt sich
nicht σ-endlich, so lässt sich 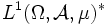 (wieder unter demselben Isomorphismus) als der Banachraum der lokal messbaren lokal im Wesentlichen beschränkten Funktionen darstellen.
(wieder unter demselben Isomorphismus) als der Banachraum der lokal messbaren lokal im Wesentlichen beschränkten Funktionen darstellen. - Der Fall p = 2 ist ein Sonderfall: Der L2 ist, falls E ein Hilbertraum ist, sogar ein Hilbertraum (siehe unten).
- Die Räume L1 und
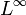 sind nicht reflexiv.
sind nicht reflexiv. - Für
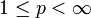 ist
ist 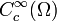 dicht in Lp(Ω).
dicht in Lp(Ω).
Verallgemeinerungen
Es gibt auch die Verallgemeinerung der Lp-Räume für 0 < p < 1. Diese sind allerdings keine Banachräume mehr, weil die entsprechende Definition keine Norm liefert, sondern nur eine Quasi-Norm. In diesem Fall ist jedoch
eine translationsinvariante Metrik auf
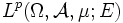 , die diesen Raum zu einem vollständigen metrischen Vektorraum macht. Die Räume Lp([0,1]) sind ein Beispiel für einen nicht lokalkonvexen, topologischen Vektorraum.
, die diesen Raum zu einem vollständigen metrischen Vektorraum macht. Die Räume Lp([0,1]) sind ein Beispiel für einen nicht lokalkonvexen, topologischen Vektorraum.Berücksichtigt man in der Norm nicht nur die Funktionswerte, sondern auch die schwachen Ableitungen, so erhält man Sobolew-Räume, die insbesondere in der Untersuchung von Differentialgleichungen eine wichtige Rolle spielen. Untersucht man statt den messbaren Funktionen nur die holomorphen beziehungsweise die harmonischen Funktionen auf Integrierbarkeit, so werden die entsprechenden Lp-Räume Hardy-Räume genannt.
Der Hilbertraum L2
Sei
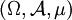 ein Maßraum,
ein Maßraum, 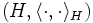 ein Hilbertraum (häufig
ein Hilbertraum (häufig  mit dem Skalarprodukt
mit dem Skalarprodukt 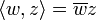 ) und
) und 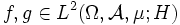 . Dann definiert
. Dann definiertein Skalarprodukt auf L2. Die von diesem Skalarprodukt induzierte Norm ist ganz offensichtlich die oben definierte L2-Norm, das heißt, dieser Raum ist bezüglich der durch das Skalarprodukt induzierten Norm vollständig und damit selbst wieder ein Hilbertraum.
Literatur
- Herbert Amann, Joachim Escher: Analysis III. 1. Auflage. Birkhäuser-Verlag Basel Boston Berlin, 2001
Wikimedia Foundation.