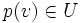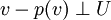Orthographische Projektion

Die Orthogonalität bezeichnet:

• in der Mathematik das Konzept des Senkrechtstehens und des rechten Winkels (daher die Benennung orthogonal aus dem Griechischen für rechtwinklig);
• in der Informatik die freie Kombinierbarkeit unabhängiger Konzepte oder die Eigenschaft eines Mikroprozessor-Befehlssatzes.
• in der Nachrichtentechnik die Unabhängigkeit der Komponenten zusammengesetzter Signale voneinander (z. B. I und Q in der Quadraturamplitudenmodulation).
• in der Systemtheorie Niklas Luhmanns die Sperrung gegenüber Informationsflüssen eines anderen Systems.

Orthogonalität in der Geometrie

Elementargeometrie

In der Elementargeometrie heißen zwei Geraden oder Ebenen orthogonal oder senkrecht zueinander, wenn sie einen rechten Winkel, d. h. einen Winkel von 90° einschließen.

Eine Gerade heißt Orthogonale auf eine Ebene, wenn ihr Richtungsvektor ein Normalenvektor der Ebene ist.

Dieses Konzept leitet sich von der Lotrichtung in der Geodäsie ab, sodass auch unspezifisch die Ausdrücke vertikal, lotrecht oder normal verwendet werden.

Analytische Geometrie

Zwei Geraden in der euklidischen Ebene sind orthogonal, wenn ihre Richtungsvektoren orthogonal sind. Im Raum oder in höheren Dimensionen wird man zusätzlich fordern, dass die beiden Geraden sich schneiden. Geraden, die einander nicht schneiden, aber nicht parallel sind, nennt man hingegen windschief. Eine Gerade und eine Ebene im Raum sind orthogonal, wenn der Richtungsvektor der Geraden orthogonal zu jedem Vektor in der Ebene ist.

Zwei Ebenen im euklidischen Raum sind orthogonal, wenn es eine Gerade gibt, die in einer der beiden Ebenen enthalten und orthogonal zur zweiten ist.

Sind zwei Geraden in der euklidischen Ebene durch die Gleichungen

y = m₁x + b₁    und   y = m₂x + b₂

gegeben, so sind sie genau dann orthogonal, wenn m₁m₂ + 1 = 0 ist, oder äquivalent: wenn 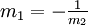$m_1 = - \tfrac 1{m_2}$ gilt.

Orthogonalität in der linearen Algebra

Orthogonale Vektoren

Allgemein gelten zwei Vektoren aus einem reellen Vektorraum, für den ein positiv definites inneres Produkt (oder Skalarprodukt) definiert ist, als orthogonal zueinander, wenn das innere Produkt der beiden Vektoren gleich 0 ist. Diese Vektorräume können zum Beispiel der 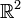$\mathbb{R}^2$ und der $\mathbb{R}^3$ sein, aber auch Funktionenräume.

Eine Menge von Vektoren nennt man orthogonal oder Orthogonalsystem, wenn alle darin enthaltenen Vektoren paarweise orthogonal zueinander sind. Eine Menge von orthogonalen Vektoren, die alle vom Nullvektor verschieden sind, ist immer linear unabhängig und bildet deshalb eine Basis der linearen Hülle dieser Menge. Wenn zusätzlich alle darin enthaltenen Vektoren die Norm 1 besitzen, nennt man die Menge ein Orthonormalsystem. Ist der Vektorraum endlichdimensional, so besitzt er immer eine Orthonormalbasis; diese lässt sich durch das Gram-Schmidtsche Orthogonalisierungsverfahren bestimmen.

Orthogonale Funktionen

In Funktionenräumen mit Skalarprodukt, wie Hilberträumen, erfolgt die Definition orthogonaler Funktionen analog, so lassen sich beispielsweise orthogonale Polynome bestimmen und auch orthogonale Basen. Allerdings sind viele interessante Räume wie die L2-Räume unendlichdimensional, siehe dazu Hilbertraumbasis. In der Quantenmechanik bilden auch die Zustände eines Systems einen Vektorraum. Entsprechend spricht man dort auch von orthogonalen Zuständen.

Orthogonale Matrix

Eine quadratische, reelle Matrix 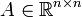$A \isin \mathbb{R}^{n \times n}$ nennt man orthogonale Matrix, wenn sie mit dem Skalarprodukt verträglich ist, wenn also für jedes Paar von Vektoren v und w die Gleichung 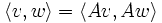$\langle v,w \rangle = \langle Av,Aw \rangle$ gilt. Die Matrix A ist genau dann orthogonal, wenn ihre Spalten (oder ihre Zeilen), als Vektoren aufgefasst, zueinander orthonormal sind (nicht nur orthogonal), anders gesagt, falls 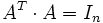$A^{T} \cdot A = I_n$ oder (gleichwertig) A^T = A ^{− 1} gilt. Die Entsprechung bei den komplexen Zahlen ist die unitäre Matrix.

Orthogonale Abbildung

Sei V ein euklidischer Vektorraum. Ein Endomorphismus 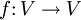$f \colon V \to V$ heißt orthogonal, wenn 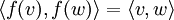$\langle f(v), f(w) \rangle = \langle v, w \rangle$ für alle 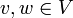$v, w \in V$ gilt. Insbesondere erhält f Längen von und Winkel zwischen Vektoren und bildet also auch orthogonale Vektoren auf orthogonale Vektoren ab. Eine Abbildung ist genau dann orthogonal, wenn ihre Matrixdarstellung bezüglich einer Orthonormalbasis eine orthogonale Matrix ist.

Die orthogonale Abbildung ist nicht zu verwechseln mit zueinander orthogonalen Abbildungen. Dabei handelt es sich um Abbildungen, die selbst als Vektoren aufgefasst werden, und deren Skalarprodukt gleich 0 ist.

Orthogonale Projektion

Ist insbesondere V ein endlichdimensionaler reeller oder komplexer Vektorraum mit einem positiv definiten Skalarprodukt, so gibt es zu jedem Unterraum U die Projektion entlang des orthogonalen Komplementes von U, welche orthogonale Projektion auf U genannt wird. Sie ist die eindeutig bestimmte Abbildung 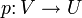$p\colon V\to U$, für die

• $p(v)\in U$

und

• $v-p(v)\perp U$

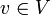für alle $v\in V$ gilt.

Ist V ein unendlichdimensionaler Hilbertraum, so gelten diese Aussagen entsprechend für abgeschlossene Unterräume U. Diese Aussage wird häufig auch als Projektionssatz bezeichnet.

Orthogonalität in der Informatik

In der Informatik ist Orthogonalität ein Entwurfsprinzip, nämlich die freie Kombinierbarkeit unabhängiger Konzepte.

Zum Beispiel galt schon in Algol 60: Wo irgendein Ausdruck eines Typs stehen darf, darf jeder beliebige Ausdruck dieses Typs stehen. Später in Fortran 66 durfte aber als (ganzzahliger) Index zur Bezeichnung eines Feld-Elements nur ein Ausdruck der Bauart „Konstante₁ mal Variable plus Konstante₂“ stehen, wobei zwei der drei Werte (samt zugehörigen Rechenzeichen) fehlen konnten. Das war ein Verstoß gegen das (viel früher formulierte) Entwurfsprinzip der Orthogonalität.

Bei Mikroprozessoren ist Orthogonalität eine bestimmte Eigenschaft des Befehlssatzes, siehe dort.

Bei magnetischen Speichermedien ist Orthogonalität eine Aufzeichnungstechnik, siehe Perpendicular Recording.

Weblinks