Variable Vakuum-Lichtgeschwindigkeit

Variable Vakuum-Lichtgeschwindigkeit

Eine physikalische Konstante oder Naturkonstante ist eine physikalische Größe, deren Größenwert sich weder räumlich noch zeitlich verändert.

Man unterscheidet zwischen elementaren oder grundlegenden (siehe auch die SI-Basiseinheiten) und abgeleiteten Konstanten, wobei die Zuordnung oft einer gewissen Willkür unterliegt. Letztere lassen sich aus den elementaren Konstanten berechnen. Beispielsweise ist der bohrsche Radius aus dem planckschen Wirkungsquantum, der Lichtgeschwindigkeit im Vakuum, der Elementarladung, der Elektronenmasse und der Protonenmasse berechenbar.

Einige Naturwissenschaften fassen wichtige Konstanten zu Gruppen von Fundamentalkonstanten zusammen, z. B. die Astronomie und Geodäsie die genauen Referenzwerte von Erd- und Sonnenmasse, den Erdradius, die Astronomische Einheit oder die Gravitationskonstante. Im strengen Sinn fundamental ist allerdings nur die letztere.

Abgeleitete und besonders phänomenologische Konstanten, wie etwa die Dauer eines Jahres, der Standardatmosphärendruck oder die Erdbeschleunigung (die allerdings örtlich um 0,5% variiert) sind dem Menschen in seiner Umgebung nützlich, haben aber in der Regel keine darüber hinausgehende Bedeutung grundlegender Art.

Inhaltsverzeichnis

Naturkonstanten-Tabelle

Bezeichnung der Konstante Symbol(e) Wert Quelle
Elektromagnetismus
Coulomb-Konstante k = 1/(4πε0) (22 468 879 468 420 441 / 2 500 000) m F−1

≈ 8,987 551 787 37 · 109 m F−1
Curie-Konstante stoffspezifisch
Elektrische Feldkonstante ε0 = 1/(μ0c02) 625 000 / (22 468 879 468 420 441 π) F m−1

≈ 8,854 187 817 62 · 10−12 F m−1 (abgeleitet)
Elementarladung e 1,602 176 487 (40) · 10−19 C [1]
von-Klitzing-Konstante RK = h/e2 25 812,807 557 (18) Ω [2]
Lichtgeschwindigkeit im Vakuum c0, c 299 792 458 m s−1 (definiert) [3]
Magnetische Feldkonstante μ0 4π · 10−7 H m−1 (definiert)

≈ 12,566 370 614 · 10−7 T2 m3 J−1
Verdet-Konstante stoffspezifisch, wellenlängenabhängig
Gravitation
Gravitationskonstante G 6,674 28 (67) · 10−11 · m3 / (kg · s2) [4]
Einsteinkonstante κ = 8πG/c4 2,07664 ·10−43 s2 / (kg · m)
Thermodynamik
Absoluter Nullpunkt T0 0 K (= −273,15 °C) (definiert)
Avogadro-Konstante NA, L 6,022 141 79 (30) · 1023 mol−1 [5]
Boltzmann-Konstante kB 1,380 650 4 (24) · 10−23 J K−1 [6]
8,617 343 (15) · 10−5 eV K−1 [7]
Loschmidt-Konstante NL, n0 (englisch) 2,686 777 4 (47) · 1025 m−3 (bei: 273,15 K und 101,325 kPa) [8]
Molvolumen eines idealen Gases, p = 1 bar, θ = 0 °C   22,710 981 (40) dm3 mol−1 [9]
Standard-Atmosphärendruck atm 101,325 kPa (definiert)
Stefan-Boltzmann-Konstante σ = 2π5 k4 / (15 h3c2) 5,670 400 (40) · 10−8 W m−2 K−4 [10]
Universelle Gaskonstante R0 = NAkB 8,314 472 (15) J K−1 mol−1 [11]
Teilchenphysik
1. (Erste) Strahlungskonstante c1 = 2π hc2 3,741 771 18 (19) · 10−16 Wm2 [12]
2. (Zweite) Strahlungskonstante c2 = hc/k 1,438 775 2 (25) · 10−2 mK [13]
Bohrscher Radius a0 = 4π ε0 ħ2 / (me e2) 5,291 772 085 9 (36) · 10−11 m [14]
Bohrsches Magneton μB = e ħ / (2 me) 9,274 009 15 (23) · 10−24 J T−1 [15]
Kernmagneton μN = e ħ / (2 mp) 5,050 783 24 (13) · 10−27 J T−1 [16]
Plancksches Wirkungsquantum h 6,626 068 96 (33) · 10−34 J s [17]
4,135 667 33 (10) · 10−15 eV s [18]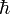
\hbar = h/(2π) 1,054 571 628 (53) · 10−34 J s [19]
Elektron
* Gyromagnetisches Verhältnis des freien Elektrons γe 1,760 859 770 (44) · 1011 s−1 T−1 [20]
* Klassischer Elektronenradius re 2,817 940 289 4 (58) · 10−15 m [21]
* Landé-Faktor des freien Elektrons ge −2,002 319 304 362 2 (15) [22]
* Magnetisches Moment μe −9,284 763 77 (23) · 10−24 JT−1 [23]
* Molare Masse Me 5,485 799 094 3 (23) · 10−7 kg mol−1 [24]
* Ruhemasse me 9,109 382 15 (45) · 10−31 kg [25]
* Spezifische Ladung e/me −1,758 820 150 (44) · 1011 C kg−1 [26]
Feinstruktur-Konstante α = μ0 e2 c0 / (2 h) 7,297 352 537 6 (50) · 10−3 [27]
α−1 137,035 999 679 (94) [28]
Neutron
* relative Atommasse n 1,008 664 915 97 (43) u [29]
* Ruhemasse mn 1,674 927 211 (84) · 10−27 kg [30]
Proton
* Gyromagnetisches Verhältnis γp 2,675 222 099 (70) · 108 s−1T−1 [31]
* Magnetisches Moment μp 1,410 606 662 (37) · 10−26 JT−1 [32]
* Magnetisches Moment in H2O μ’p/μB 1,520 993 132 (16) · 10−3
* Resonanzfrequenz per Feld in H2O γ'p/2π 42,576 375 (13) MHzT−1
* Ruhemasse mp 1,672 621 637 (83) · 10−27 kg [33]
Rydberg-Energie R∞ch 13,605 691 93 (34) eV [34]
Rydberg-Frequenz R∞c 3,289 841 960 361 (22) · 1015 s−1 [35]
Rydberg-Konstante R∞ = e4 me / (8 ε02 h3 c) 1,097 373 156 852 7 (73) · 107 m−1 [36]
Verhältnis von Protonen- zu Elektronenmasse mp/me 1 836,152 672 47 (80) [37]
Vermischtes
Atomare Masseneinheit mu, amu, u (g · NA−1) 1,660 538 782 (83) · 10−27 kg [38]
Faraday-Konstante F (e · NA) 96 485,339 9 (24) C mol−1 [39]
(Gregorianisches) Jahr a 365,242 5 d (definiert)
Hartree-Energie Eh 4,359 743 94 (22) · 10−18 J [40]
Magnetisches Flussquantum Φ0 = h/(2e) 2,067 833 667 (52) · 10−15 Wb [41]

Die Ziffern in Klammern hinter einem Zahlenwert bezeichnen die Unsicherheit in den letzten Stellen des Wertes. (Beispiel: Die Angabe 6,674 28 (67) ist gleichbedeutend mit 6,674 28 ± 0,000 67.) Die Unsicherheit ist als einfache Standardabweichung gegeben.

Konstanz der Naturkonstanten

Ob die Naturkonstanten auch über astronomische Zeiträume hinweg wirklich konstant sind, ist Gegenstand aktueller Forschung. So schienen Messungen der Spektrallinien von Quasaren mit dem Keck-Teleskop auf Hawaii auf eine leichte Abnahme der Feinstrukturkonstante um etwa ein hundertstel Promille im Verlauf von zehn Milliarden Jahren hinzudeuten. Dieses Resultat war von Anfang an umstritten; zum einen wiesen Forscher auf die unsichere Fehlerabschätzung der Datenauswertung hin, zum anderen gibt es Daten aus der Oklo-Mine in Westafrika, wo vor etwa 2 Milliarden Jahren Uran so stark angehäuft war, dass eine natürliche Kettenreaktion stattfand. Nach diesen Daten hatte die Feinstrukturkonstante damals denselben Zahlenwert wie heute. Neuere Messungen der Spektrallinien von Quasaren mit dem Very Large Telescope der Europäischen Südsternwarte in Chile widersprechen den früheren Resultaten am Keck-Teleskop und weisen auf die Konstanz der Feinstrukturkonstante hin.

Inzwischen sind Präzisionsmessungen möglich, die stetige Schwankungen in der Größenordnung, wie sie die Beobachtungen mit dem Keck-Teleskop nahelegen, auch im Labor in kurzen Zeiträumen überprüfen können. Untersuchungen von Theodor Hänsch und seiner Arbeitsgruppe am MPI für Quantenoptik belegen die Konstanz der Feinstrukturkonstante mit einer Genauigkeit von 15 Nachkommastellen über einen Zeitraum von vier Jahren.

Veränderung der Angaben durch neue Messungen

Wie sich die Angaben der Naturkonstanten durch immer genauere Messungen ändern, hält das Committee on Data for Science and Technology, kurz CODATA, in Dokumenten fest. Das eng mit CODATA zusammenarbeitende National Institute of Standards and Technology (NIST) in den USA veröffentlicht bereits seit einiger Zeit online PDF-Dokumente mit aktuellen Abschätzungen der Werte der physikalischen Konstanten, darunter auch ältere Dokumente, mit denen sich z. B. alle Veränderungen im Zeitraum von 1986 bis 2006 erfassen lassen.

Siehe auch

Feinabstimmung der Naturkonstanten

Weblinks

Literatur

  • Harald Fritzsch: Das absolut Unveränderliche: die letzten Rätsel der Physik. Piper, München; Zürich 2005, ISBN 978-3-492-04684-8
  • John D. Barrow: Das 1x1 des Universums: Neue Erkenntnisse über die Naturkonstanten. Rowohlt Taschenbuch Verlag, Reinbek bei Hamburg 2006, ISBN 978-3-499-62060-7
  • P.J. Mohr, B.N. Taylor: CODATA recommended values of the fundamental physical constants: 1998, Rev. Mod. Phys. vol. 72 (2000), 351-495 online
  • P.J. Mohr, B.N. Taylor: CODATA recommended values of the fundamental physical constants: 2002, Rev. Mod. Phys. vol. 77 (2005), 1-107, doi:10.1103/RevModPhys.77.1
  • maßstäbe 7 – Die Unveränderlichen- Magazin der PTB, Ausgabe Sept. 2006

Einzelnachweise

  1. ↑ CODATA 2006 [1], 12.09.2007
  2. ↑ CODATA 2006 [2], 12.09.2007
  3. ↑ CODATA 2006 [3], 27.07.2008
  4. ↑ CODATA 2006 [4], 12.09.2007
  5. ↑ CODATA 2006 [5], 12.09.2007
  6. ↑ CODATA 2006 [6], 12.09.2007
  7. ↑ CODATA 2006 [7], 12.09.2007
  8. ↑ CODATA 2006 [8], 12.09.2007
  9. ↑ CODATA 2006 [9], 12.09.2007
  10. ↑ CODATA 2006 [10], 12.09.2007
  11. ↑ CODATA 2006 [11], 12.09.2007
  12. ↑ CODATA 2006 [12], 12.09.2007
  13. ↑ CODATA 2006 [13], 12.09.2007
  14. ↑ CODATA 2006 [14], 12.09.2007
  15. ↑ CODATA 2006 [15], 12.09.2007
  16. ↑ CODATA 2006 [16], 12.09.2007
  17. ↑ CODATA 2006 [17], 12.09.2007
  18. ↑ CODATA 2006 [18], 12.09.2007
  19. ↑ CODATA 2006 [19], 12.09.2007
  20. ↑ CODATA 2006 [20], 12.09.2007
  21. ↑ CODATA 2006 [21], 12.09.2007
  22. ↑ CODATA 2006 [22], 12.09.2007
  23. ↑ CODATA 2006 [23], 12.09.2007
  24. ↑ CODATA 2006 [24], 12.09.2007
  25. ↑ CODATA 2006 [25], 12.09.2007
  26. ↑ CODATA 2006 [26], 12.09.2007
  27. ↑ CODATA 2006 [27], 12.09.2007
  28. ↑ CODATA 2006 [28], 12.09.2007
  29. ↑ CODATA 2006 [29], 12.09.2007
  30. ↑ CODATA 2006 [30], 12.09.2007
  31. ↑ CODATA 2006 [31], 12.09.2007
  32. ↑ CODATA 2006 [32], 12.09.2007
  33. ↑ CODATA 2006 [33], 12.09.2007
  34. ↑ CODATA 2006 [34], 14.09.2007
  35. ↑ CODATA 2006 [35], 12.09.2007
  36. ↑ CODATA 2006 [36], 12.09.2007
  37. ↑ CODATA 2006 [37], 12.09.2007
  38. ↑ CODATA 2006 [38], 12.09.2007
  39. ↑ CODATA 2006 [39], 12.09.2007
  40. ↑ CODATA 2006 [40], 12.09.2007
  41. ↑ CODATA 2006 [41], 12.09.2007

Wikimedia Foundation.

Игры ⚽ Нужна курсовая?

Schlagen Sie auch in anderen Wörterbüchern nach:

  • Variable Lichtgeschwindigkeit — Eine physikalische Konstante oder Naturkonstante ist eine physikalische Größe, deren Größenwert sich weder räumlich noch zeitlich verändert. Man unterscheidet zwischen elementaren oder grundlegenden (siehe auch die SI Basiseinheiten) und… …   Deutsch Wikipedia

  • Überlichtgeschwindigkeit — Als Überlichtgeschwindigkeit wird eine Geschwindigkeit bezeichnet, welche größer als die Vakuum Lichtgeschwindigkeit (299.792.458 m/s) ist. Die Geschwindigkeit schneller als Licht in optisch dichten Medien ist im Artikel Lichtgeschwindigkeit …   Deutsch Wikipedia

  • Spezielle Relativitätstheorie — Die spezielle Relativitätstheorie (kurz: SRT) ist eine physikalische Theorie über Raum und Zeit. Sie verallgemeinert das galileische Relativitätsprinzip der klassischen Mechanik auf alle Gesetze der Physik. Dieses Prinzip besagt, dass in allen… …   Deutsch Wikipedia

  • Speziellen Relativitätstheorie — Die spezielle Relativitätstheorie (kurz: SRT) ist eine physikalische Theorie über Raum und Zeit. Sie verallgemeinert das galileische Relativitätsprinzip der klassischen Mechanik, welches besagt, dass in allen relativ zueinander gleichförmig… …   Deutsch Wikipedia

  • Zur Elektrodynamik bewegter Körper — Die spezielle Relativitätstheorie (kurz: SRT) ist eine physikalische Theorie über Raum und Zeit. Sie verallgemeinert das galileische Relativitätsprinzip der klassischen Mechanik, welches besagt, dass in allen relativ zueinander gleichförmig… …   Deutsch Wikipedia

  • Ionosphäre — Beziehung von Ionosphäre und Erdatmosphäre …   Deutsch Wikipedia

  • Maxwell-Gleichungen — Die Maxwell Gleichungen von James Clerk Maxwell beschreiben die Phänomene des Elektromagnetismus. Sie sind damit ein wichtiger Teil des modernen physikalischen Weltbilds. Die Maxwell Gleichungen sind ein spezielles System von linearen partiellen… …   Deutsch Wikipedia

  • Maxwell'sche Gleichungen — Die vier maxwellschen Gleichungen beschreiben die Erzeugung von elektrischen und magnetischen Feldern durch Ladungen und Ströme, sowie die Wechselwirkung zwischen diesen beiden Feldern, die bei zeitabhängigen Feldern als Zeitentwicklung in… …   Deutsch Wikipedia

  • Maxwell-Gleichung — Die vier maxwellschen Gleichungen beschreiben die Erzeugung von elektrischen und magnetischen Feldern durch Ladungen und Ströme, sowie die Wechselwirkung zwischen diesen beiden Feldern, die bei zeitabhängigen Feldern als Zeitentwicklung in… …   Deutsch Wikipedia

  • Maxwell Gleichungen — Die vier maxwellschen Gleichungen beschreiben die Erzeugung von elektrischen und magnetischen Feldern durch Ladungen und Ströme, sowie die Wechselwirkung zwischen diesen beiden Feldern, die bei zeitabhängigen Feldern als Zeitentwicklung in… …   Deutsch Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”