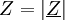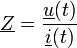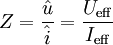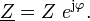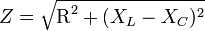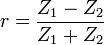Widerstandsoperator

Physikalische Größe
Name	Impedanz
Formelzeichen der Größe	Z
Größen- und Einheiten- system Einheit Dimension SI Ohm (Ω) M·L2/(I2·T3)
Siehe auch: elektrischer Widerstand

Die Impedanz (von lateinisch impedire = hemmen, hindern) ist in der Elektrotechnik der Wechselstromwiderstand. Dieser Widerstand ist die Eigenschaft

• eines Bauelementes, genau gesagt eines linearen passiven Zweipols, beim Fluss eines elektrischen Wechselstromes (siehe auch komplexe Wechselstromrechnung),
• einer Leitung oder eines Mediums bei der elektromagnetischen (oder auch akustischen) Wellenausbreitung (siehe auch Wellenimpedanz). Bei der Wellenausbreitung ist kein konkretes Bauelement an diesem Widerstand beteiligt, weder ein Wirk- noch ein Blindwiderstand.

Die Impedanz ist in der Wechselstromtechnik die Zusammenfassung von zwei Aussagen.

1. Sie gibt das Verhältnis der Amplituden von sinusförmiger Wechselspannung zu sinusförmigem Wechselstrom an.
   
2. Sie gibt die Phasenverschiebung zwischen diesen beiden Größen an.
   

Die Zusammenfassung erfolgt mathematisch durch Darstellung der Impedanz als komplexe Größe mit dem Formelzeichen $\underline Z$.

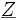Der Betrag der komplexen Impedanz 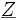$\underline Z$ ist der Scheinwiderstand $Z\$:

$Z = |\underline Z| \,$

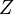Die zeitliche Verschiebung wird durch den Phasenverschiebungswinkel φ angegeben. Während er bei einem Wirkwiderstand immer null ist, kann er bei einer beliebigen Impedanz Werte zwischen –90° und +90° annehmen.

Der Kehrwert der Impedanz ist die Admittanz 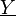$\underline Y$ (komplexer Leitwert).

Die Impedanzen und ihre unterschiedlichen Namen

Ri	Ra
Innenwiderstand	Außenwiderstand
Quellwiderstand	Lastwiderstand
Ausgangswiderstand	Eingangswiderstand
Wellenimpedanz	Abschlusswiderstand

Berechnung

Analog zum ohmschen Gesetz, bei dem der elektrische Widerstand der Quotient aus Gleichspannung und Gleichstrom ist, ist die Impedanz der Quotient aus der komplexen, zeitabhängigen Wechselspannung 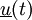$\underline u(t)$ und des komplexen, zeitabhängigen Wechselstroms 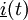$\underline i(t)$ . (Zur Darstellung einer Wechselgröße als komplexe Wechselgröße siehe Komplexe Wechselstromrechnung.)

$\underline Z = {\underline {u}(t) \over \underline {i}(t)} \,$

Sie ergibt sich jedoch nicht als Quotient aus der reellen zeitabhängigen Wechselspannung 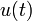$u(t)\,$ und des reellen zeitabhängigen Wechselstroms $i(t)\,$ .

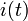Der Betrag der komplexen Impedanz, der Scheinwiderstand Z, ergibt sich als Quotient aus den Amplituden oder den Effektivwerten der zeitabhängigen Wechselspannung 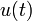$u(t)\,$ und des zeitabhängigen Wechselstroms $i(t)\,$ :

$Z = \frac{\hat u}{\hat i} = \frac{U_\mathrm{eff}}{I_\mathrm{eff}}$

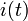Sofern es sich nicht um Leitungsimpedanzen handelt, werden Strom und Spannung durch andere, entsprechende Größen ersetzt. Bei der elektromagnetischen Wellenimpedanz die Spannung durch die Feldstärke und der Strom durch die magnetische Flussdichte sowie in der Akustik die Spannung durch den Schalldruck und der Strom durch die Schallschnelle.

Anwendung

Impedanzverlauf einer Lautsprecherbox als Funktion der Frequenz

Die Impedanz hat große Bedeutung bei der Anpassung von Hochfrequenzleitungen, aber auch bei der Wellenausbreitung im freien Raum. Wenn zum Beispiel die Eingangsimpedanz eines Gerätes nicht mit der Impedanz der Leitung übereinstimmt, kommt es zu Reflexionen, was die Leistungsübertragung mindert und was zu Resonanzerscheinungen und damit zu einem nichtlinearen Frequenzgang führen kann. Bei Übertragungen auf einer Leitung mit erheblich weniger als einer Wellenlänge (Stromversorgungsleitungen, Lautsprecherleitungen) spielt dieses keine Rolle.

Elektrodynamische Lautsprecher werden stets mit Wechselstrom betrieben, deshalb verursacht der induktive Widerstand der eingebauten Schwingspule eine gewisse Phasenverschiebung zwischen Strom und Spannung, die frequenzabhängig ist. Aus diesem Grund spricht man nicht vom Widerstand, sondern von der Impedanz des Lautsprechers. Dessen Wert kann eine komplizierte Funktion der Frequenz sein.

Werden Impulse oder HF-Signale durch Kabel übertragen, hat ein ohmscher Widerstand der Leitung geringen Bezug zur Impedanz des Kabels. Hier kommt es fast immer darauf an, Reflexionen der Impulse am entgegengesetzten Ende des Kabels zu vermeiden. Der dazu nötige Abschlusswiderstand ist für hinreichend hohe Frequenzen praktisch reell, also ein ohmscher Widerstand. Dieser Wert wird als Leitungswellenwiderstand oder als Wellenimpedanz des Kabels bezeichnet. Für niedrige Frequenzen ist der Leitungswellenwiderstand komplexwertig und stark frequenzabhängig. Dieser Widerstand kann mittels Zeitbereichsreflektometrie ermittelt werden.

In der Biologie kann mittels Electric Cell-Substrate Impedance Sensing die Impedanz genutzt werden, um Formveränderungen bei tierischen Zellen nachzuweisen.

Darstellung

Die Impedanz als Wechselstromwiderstand hat die Einheit Ohm mit dem Einheitenzeichen Ω. Sie ist eine komplexe Größe und wird üblicherweise mit dem (Zeiger-)Symbol 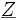$\underline Z$ benannt und graphisch mittels eines Zeigerdiagramms abgebildet.

In der Darstellung der Impedanz als komplexe Größe lassen sich ihre Bestandteile und deren Bedeutung ablesen:

• Bei der Formulierung in kartesischen Koordinaten bildet der ohmsche Widerstand R als (für die Übertragung der Wirkleistung relevanter) Wirkwiderstand den Realteil, während im Imaginärteil der Blindwiderstand X vorkommt (der keine Wirkleistung umsetzt, sondern gespeicherte Energie mit Phasenverschiebung an den Generator zurückspeist):

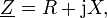$\underline Z = R + \mathrm{j}X,$ wobei j die imaginäre Einheit ist.

• Bei der Formulierung in Polarkoordinaten steht der Betrag der komplexen Zahl 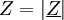$Z = |\underline Z|$ (als Länge des Zeigers im Zeigerdiagramm) für den Scheinwiderstand, also den Widerstand, den man nach einer Messung von Strom und Spannung mit dem ohmschen Gesetz als Z = U / I errechnen würde; die Winkelangabe φ bildet die Phasenverschiebung zwischen Strom I und Spannung U :

$\underline Z = Z \ e^{\mathrm{j} \varphi}.$

Rein induktive Komponenten haben keinen Wirkwiderstand und einen Phasenverschiebungswinkel von

$\varphi = +90^\circ = +\pi/2$ ,

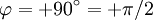also einen Zeiger auf der positiven vertikalen Achse bzw. einen positiven (induktiven) Blindwiderstand X_L, auch Induktanz genannt, denn die Spannung eilt dem Strom um 90° vor. Rein kapazitive Komponenten haben hingegen einen negativen (kapazitiven) Blindwiderstand X_C, auch Kapazitanz genannt und werden durch Zeiger auf der negativen vertikalen Achse (X_C < 0,R = 0) abgebildet (Spannung um 90° dem Strom nacheilend). Auch bei einem nicht verschwindenden Wirkanteil lässt sich entsprechend ablesen, ob sich die Komponente induktiv (Zeiger im ersten (oberen rechten) Quadranten des Koordinatensystems, positiver Imaginärteil, 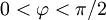$0 &amp;amp;lt; \varphi &amp;amp;lt; \pi /2$ ) oder kapazitiv (Zeiger im vierten (unteren rechten) Quadranten, negativer Imaginärteil, 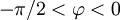$-\pi /2&amp;amp;lt; \varphi &amp;amp;lt; 0$ ) verhält.

Grafische Darstellung der Berechnung des Scheinwiderstandes im Zeigerdiagramm

Der Scheinwiderstand ist dementsprechend der Betrag der geometrischen (komplexen) Addition des Wirk- und der Blindwiderstände:

$Z=\sqrt{\mbox{R}^2 + (X_L - X_C)^2}$

Bei technischen Geräten wird häufig nur dieser Betrag der Impedanz 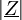$|\underline Z|$ , also der Scheinwiderstand, angegeben. In einem allgemeinen Netzwerk aus ohmschen Widerständen, Induktivitäten und Kapazitäten ist dieser jedoch frequenzabhängig.

Lautsprecher haben stark frequenzabhängige Impedanzen – es wird jedoch ein Nennwert (z. B. 4 Ω oder 8 Ω) angegeben. Nach internationalem Standard (IEC 60268) darf die im Frequenzbereich vorkommende niedrigste Impedanz diesen Nennwert um nicht mehr als 20 % unterschreiten. Höhere Impedanzen bei anderen Frequenzen sind beliebig zulässig.

Bei Hochfrequenz-Kabeln wird die (bauartbedingte) Kennimpedanz als Wellenwiderstand bezeichnet. Er beträgt bei Koaxialkabeln 50 Ω bis 100 Ω und bei symmetrischen (Zweidraht-)Leitungen 110 Ω bis 300 Ω.

Bei Antennen nennt man die Eingangsimpedanz auch Fußpunktwiderstand, er sollte bei der Frequenz, für welche die Antenne vorgesehen ist, real sein und mit der Impedanz des Kabels übereinstimmen (z. B. 60 Ω oder 240 Ω).

Die Quellimpedanz eines Hochfrequenz-Senders sollte möglichst gut mit der Kabel- und Antennenimpedanz übereinstimmen, da es sonst zu Reflexionen an den Enden des Kabels kommt, die den Sender beschädigen oder zerstören können. Dagegen muss die Quellimpedanz eines NF-Verstärkers sehr viel kleiner als diejenige der Lautsprecher sein, um deren Eigenresonanzen zu bedämpfen; dieses wird Anpassung oder genauer Spannungsanpassung genannt. Fehlanpassungen können durch Impedanzanpassung behoben werden.

Impedanzanpassung

Bei Übertragungen kommt es zu Reflexionen von Wellen, wenn sich die Impedanz einer Leitung oder des Übertragungsmittels ändert. Dies ist grundsätzlich nicht an die Anzahl der Wellenlängen auf einer Leitung gebunden, bei im Verhältnis zur Wellenlänge kurzen Übertragungswegen wirkt sich aber die Änderung der Impedanz des Übertragungsmittels kaum aus. Am Ort der Impedanzänderung wird ein Teil der ankommenden Welle reflektiert. Der Betrag des Reflektionsfaktors r liegt zwischen 0 und 1. Wenn sein Betrag 1 ist, wird die gesamte Welle reflektiert und bei r = 0 (das bedeutet Z₁ = Z₂) tritt keine Reflexion auf, man spricht in diesem Fall von Impedanzanpassung. Impedanzanpassung ist bei Hochfrequenzleitungen und bei der elektromagnetischen Wellenausbreitung oft erwünscht.

$r = \frac{Z_1 -Z_2}{Z_1 +Z_2} \,$

Literatur

• Adolf J. Schwab: Elektroenergiesysteme – Erzeugung, Transport, Übertragung und Verteilung elektrischer Energie. Springer Verlag, 2006, ISBN 3-540-29664-6.
• Jürgen Detlefsen, Uwe Siart: Grundlagen der Hochfrequenztechnik. 2. Auflage. Oldenbourg Verlag, München Wien 2006, ISBN 3-486-57866-9.
• Wolfgang-Josef Tenbusch: Grundlagen der Lautsprecher. 1. Auflage. Michael E. Brieden Verlag, Oberhausen 1989, ISBN 3-9801851-0-9.

Siehe auch

• Dämpfungsfaktor
• Impedanzwandler
• Impedanzspektroskopie
• Cole-Cole-Plot
• Ausgangsimpedanz
• Akustische Impedanz

Weblinks

• Impedanzen, Widerstände – Ri, Ra und Re und Schnittstelle – pdf
• 8-Ohm-Verstärker mit 4-Ohm-Boxen?! – pdf
• Größe der Impedanzen in der Tontechnik – pdf