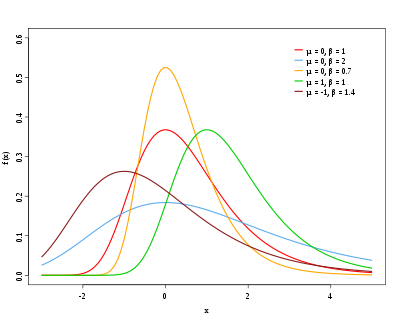
Gumbel-Verteilung

Die Gumbel-Verteilung oder Extremal–I–Verteilung ist als eine stetige Wahrscheinlichkeitsverteilung eine der drei für die Extremwerttheorie wichtigen Wahrscheinlichkeitsverteilungen. Sie wurde benannt nach Emil Julius Gumbel. Wie die Rossi-Verteilung und die Frechet-Verteilung gehört sie zu den Extremwertverteilungen, die den in einem Zeitraum T zu erwartenden höchsten Messwert berechnen.

Sie wird u.a. in folgenden Bereichen benutzt:

• Wasserwirtschaft für extreme Ereignisse wie Hochwasser und Trockenzeiten
• Verkehrsplanung
• Meteorologie (Wettervorhersage)
• Hydrologie

Die Gumbel–Verteilung ist eine typische Verteilungsfunktion für jährliche Serien. Sie kann nur auf Reihen angewendet werden, bei denen die Länge der Meßreihe mit dem Stichprobenumfang übereinstimmt. Ansonsten erhält man negative Logarithmen.

Definition

Dichtefunktion der Gumbel-Verteilung

Eine stetige Zufallsgröße X genügt einer Gumbel-Verteilung, wenn sie die Wahrscheinlichkeitsdichte

$f(x)= \mathrm{e}^{-x} \mathrm{e}^{-\mathrm{e}^{-x}},~ x\in\mathbb{R}$

und damit die Verteilungsfunktion

$F(x)= \mathrm{e}^{-\mathrm{e}^{-x}},~ x\in\mathbb{R}$

besitzt.

Eigenschaften

Erwartungswert

Die Gumbelverteilung besitzt den Erwartungswert

$\operatorname{E}(X) = \gamma$.

Dabei ist $\gamma \approx 0,5772$ die Euler-Mascheroni-Konstante.

Varianz

Die Varianz ergibt sich analog zu

$\operatorname{Var}(X) = \frac{\pi^{2}}{6}$.

Standardabweichung

Daraus erhält man für die Standardabweichung

$\sigma = \frac{\pi}{\sqrt{6}}$.

Verallgemeinerung

Durch die affin-linearen Transformationen $X \mapsto Y := a + bX$ erhält man eine ganze Klasse von Verteilungen, auch Fisher-Tippett-Verteilung genannt, mit den Eigenschaften

$F_Y(x) = F\left(\frac{x-a}{b}\right)$

$f_Y(x) = \frac{1}{b} f\left(\frac{x-a}{b}\right)$

$\operatorname{E}(Y) = b \operatorname{E}(X) + a$

$\operatorname{Var}(Y) = b^2 \operatorname{Var}(X)$.

Beziehung zu anderen Verteilungen

Beziehung zur Extremwertverteilung

Die Gumbel-Verteilung ergibt sich aus der Extremwertverteilung mit den Parametern a = 0, b = 1 und c = 1.

Beziehung zur Fisher-Tippett-Verteilung

Die Gumbel-Verteilung ist äquivalent zur Fisher-Tippett-Verteilung mit den Parametern a = 0 und b = 1.

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli | beta-binomial | binomial | kategorial | hypergeometrisch | Rademacher | Zipf | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | negativ binomial | erweitert negativ binomial | Compound-Poisson | diskret uniform | discrete-Phase-Type | Gauss-Kuzmin | geometrisch | logarithmisch | parabolisch-fraktal | Poisson | Poisson-Gamma | Skellam | Yule-Simon | Zeta