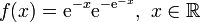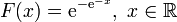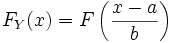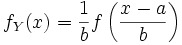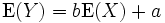- Gumbelverteilung
-
Die Gumbel-Verteilung ist als eine stetige Wahrscheinlichkeitsverteilung eine der drei für die Extremwerttheorie wichtigen Wahrscheinlichkeitsverteilungen. Sie wurde benannt nach Emil Julius Gumbel. Wie die Rossi-Verteilung und die Frechet-Verteilung gehört sie zu den Extremwertverteilungen, die den in einem Zeitraum T zu erwartenden höchsten Messwert berechnen.
Sie wird u.a. in folgenden Bereichen benutzt:
- Wasserwirtschaft für extreme Ereignisse wie Hochwasser und Trockenzeiten
- Verkehrsplanung
- Meteorologie (Wettervorhersage)
- Hydrologie
Inhaltsverzeichnis
Definition
Eine stetige Zufallsgröße X genügt einer Gumbel-Verteilung, wenn sie die Wahrscheinlichkeitsdichte
und damit die Verteilungsfunktion
besitzt.
Eigenschaften
Erwartungswert
Die Gumbelverteilung besitzt den Erwartungswert
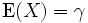 .
.
Dabei ist
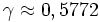 die Euler-Mascheroni-Konstante.
die Euler-Mascheroni-Konstante.Varianz
Die Varianz ergibt sich analog zu
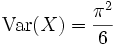 .
.
Standardabweichung
Daraus erhält man für die Standardabweichung
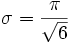 .
.
Verallgemeinerung
Durch die affin-linearen Transformationen
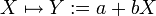 erhält man eine ganze Klasse von Verteilungen, auch Fischer-Tippett-Verteilung genannt, mit den Eigenschaften
erhält man eine ganze Klasse von Verteilungen, auch Fischer-Tippett-Verteilung genannt, mit den Eigenschaften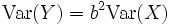 .
.
Beziehung zu anderen Verteilungen
Beziehung zur Extremwertverteilung
Die Gumbel-Verteilung ergibt sich aus der Extremwertverteilung mit den Parametern a = 0, b = 1 und c = 1.
Beziehung zur Fisher-Tippett-Verteilung
Die Gumbel-Verteilung ist äquivalent zur Fisher-Tippett-Verteilung mit den Parametern a = 0 und b = 1.
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.