- Satz von Komura
-
Unter einem nuklearen Raum versteht man in der Mathematik eine spezielle Klasse lokalkonvexer Vektorräume. Viele in den Anwendungen wichtige Räume, z. B. Räume differenzierbarer Funktionen, sind nuklear. Während normierte Räume, insbesondere Banachräume oder Hilberträume, Verallgemeinerungen endlich-dimensionaler Vektorräume über
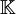 (
(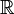 oder
oder 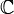 ) unter Beibehaltung der Norm aber unter Verlust von Kompaktheitseigenschaften darstellen, liegt der Schwerpunkt bei den nuklearen Räumen, die im unendlich-dimensionalen Fall nicht normierbar sind, auf den Kompaktheitseigenschaften. Ferner erweisen sich unbedingte Konvergenz und absolute Konvergenz von Reihen in nuklearen Räumen als äquivalent. In diesem Sinne sind die nuklearen Räume näher an den endlich-dimensionalen Räumen als die Banachräume.
) unter Beibehaltung der Norm aber unter Verlust von Kompaktheitseigenschaften darstellen, liegt der Schwerpunkt bei den nuklearen Räumen, die im unendlich-dimensionalen Fall nicht normierbar sind, auf den Kompaktheitseigenschaften. Ferner erweisen sich unbedingte Konvergenz und absolute Konvergenz von Reihen in nuklearen Räumen als äquivalent. In diesem Sinne sind die nuklearen Räume näher an den endlich-dimensionalen Räumen als die Banachräume.Die auf Alexander Grothendieck zurückgehenden nuklearen Räume lassen sich auf vielfältige Weise einführen. Als Definition wird hier die am einfachsten formulierbare Variante gewählt, anschließend folgt eine Liste äquivalenter Charakterisierungen, die gleichzeitig eine Reihe wichtiger Eigenschaften nuklearer Räume darstellt. Es folgen Beispiele und weitere Eigenschaften.
Inhaltsverzeichnis
Definition
Ein lokalkonvexer Raum E (immer als Hausdorffraum angenommen) heißt nuklear, wenn für jeden Banachraum F jeder stetige lineare Operator
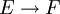 ein nuklearer Operator ist.
ein nuklearer Operator ist.Charakterisierungen
Kanonische Abbildungen
Ist p eine stetige Halbnorm auf dem lokalkonvexen Raum E, so ist
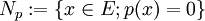 ein abgeschlossener Unterraum von E und durch
ein abgeschlossener Unterraum von E und durch 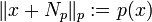 wird eine Norm auf dem Faktorraum Ep: = E / Np erklärt. Die Vervollständigung dieses normierten Raums wird mit Bp bezeichnet. Ist q eine weitere stetige Halbnorm mit
wird eine Norm auf dem Faktorraum Ep: = E / Np erklärt. Die Vervollständigung dieses normierten Raums wird mit Bp bezeichnet. Ist q eine weitere stetige Halbnorm mit 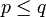 , so definiert
, so definiert 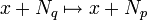 einen stetigen linearen Operator
einen stetigen linearen Operator 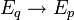 , der sich stetig zu einem linearen Operator
, der sich stetig zu einem linearen Operator 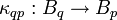 fortsetzen lässt. Die Bp heißen die lokalen Banachräume und die Operatoren κqp heißen kanonische Abbildungen von E.
fortsetzen lässt. Die Bp heißen die lokalen Banachräume und die Operatoren κqp heißen kanonische Abbildungen von E.Mit diesen Begriffen gelingt eine innere Charakterisierung nuklearer Räume, d.h. ohne Bezugnahme auf andere Räume:
- Ein lokalkonvexer Raum ist genau dann nuklear, wenn es zu jeder stetigen Halbnorm p eine weitere stetige Halbnorm
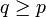 gibt, so dass die kanonische Abbildung κqp ein nuklearer Operator ist.
gibt, so dass die kanonische Abbildung κqp ein nuklearer Operator ist.
Es genügt natürlich, sich auf ein gerichtetes System erzeugender Halbnormen zu beschränken.
Hilberträume
Die nun folgenden Charakterisierungen rücken die nuklearen Räume in die Nähe von Hilberträumen.
- Ein lokalkonvexer Raum ist genau dann nuklear, wenn es ein gerichtetes System
 erzeugender Halbnormen gibt, so dass jeder lokale Banachraum
erzeugender Halbnormen gibt, so dass jeder lokale Banachraum 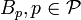 , ein Hilbertraum ist und es zu jedem
, ein Hilbertraum ist und es zu jedem 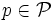 ein
ein  , gibt, so dass die kanonische Abbildung κqp ein Hilbert-Schmidt-Operator ist.
, gibt, so dass die kanonische Abbildung κqp ein Hilbert-Schmidt-Operator ist.
Ist
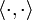 eine Hermitesche Form auf E mit
eine Hermitesche Form auf E mit 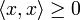 für alle
für alle  (d.h. die Hermitesche Form ist nicht-negativ), so ist durch
(d.h. die Hermitesche Form ist nicht-negativ), so ist durch 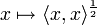 eine Halbnorm auf E definiert. Solche Halbnormen nennt man Hilbert-Halbnormen.
eine Halbnorm auf E definiert. Solche Halbnormen nennt man Hilbert-Halbnormen.- Ein lokalkonvexer Raum ist genau dann nuklear, wenn es ein gerichtetes System erzeugender Hilbert-Halbnormen gibt.
Tensorprodukte
Es gibt zwei wichtige Methoden, das Tensorprodukt
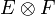 zweier lokalkonvexer Räume mit einer geeigneten lokalkonvexen Topologie auszustatten. Seien
zweier lokalkonvexer Räume mit einer geeigneten lokalkonvexen Topologie auszustatten. Seien 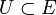 und
und  abgeschlossene, absolutkonvexe Nullumgebungen. πU,V sei das Minkowski-Funktional der absolutkonvexen Hülle von
abgeschlossene, absolutkonvexe Nullumgebungen. πU,V sei das Minkowski-Funktional der absolutkonvexen Hülle von  . Weiter bezeichne
. Weiter bezeichne 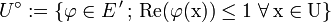 die Polare von U und analog
die Polare von U und analog 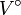 die Polare von V. Man erhält eine weitere Halbnorm εU,V auf
die Polare von V. Man erhält eine weitere Halbnorm εU,V auf 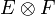 durch die Definition
durch die Definition  .
.Das projektive Tensorprodukt oder π-Tensorprodukt
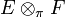 ist der Tensorproduktraum mit dem System der Halbnormen πU,V, wobei
ist der Tensorproduktraum mit dem System der Halbnormen πU,V, wobei 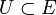 und
und  die abgeschlossenen, absolutkonvexen Nullumgebungen durchlaufen. Entsprechend ist das injektive Tensorprodukt oder ε-Tensorprodukt
die abgeschlossenen, absolutkonvexen Nullumgebungen durchlaufen. Entsprechend ist das injektive Tensorprodukt oder ε-Tensorprodukt 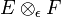 der mit dem System der Halbnormen εU,V ausgestattete Tensorproduktraum.
der mit dem System der Halbnormen εU,V ausgestattete Tensorproduktraum.Leicht überlegt man sich, dass stets
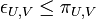 gilt, d.h.
gilt, d.h. 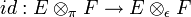 ist stetig. Diese Abbildung ist im Allgemeinen kein Homöomorphismus. Es gilt:
ist stetig. Diese Abbildung ist im Allgemeinen kein Homöomorphismus. Es gilt:- Ein lokalkonvexer Raum E ist genau dann nuklear, wenn
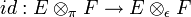 für jeden lokalkonvexen Raum ein Homöomorphismus ist.
für jeden lokalkonvexen Raum ein Homöomorphismus ist.
- Ein lokalkonvexer Raum E ist genau dann nuklear, wenn
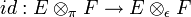 für jeden Banachraum ein Homöomorphismus ist.
für jeden Banachraum ein Homöomorphismus ist.
- Ein lokalkonvexer Raum E ist genau dann nuklear, wenn
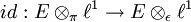 ein Homöomorphismus ist.
ein Homöomorphismus ist.
Diese Charakterisierung ist die ursprüngliche von Grothendieck verwendete Definition der Nuklearität.
Bilinearformen
Ist
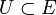 eine absolutkonvexe Nullumgebung, so ist die Polare
eine absolutkonvexe Nullumgebung, so ist die Polare  eine absolutkonvexe und absorbierende Menge im Vektorraum
eine absolutkonvexe und absorbierende Menge im Vektorraum 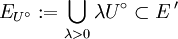 ,
, 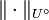 sei das zugehörige Minkowski-Funktional. Eine Bilinearform
sei das zugehörige Minkowski-Funktional. Eine Bilinearform 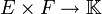 heißt nuklear, falls es absolutkonvexe Nullumgebungen
heißt nuklear, falls es absolutkonvexe Nullumgebungen 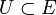 und
und  gibt und Folgen (an)n in
gibt und Folgen (an)n in 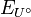 und (bn)n in
und (bn)n in  gibt mit
gibt mit 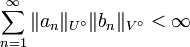 und
und 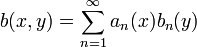 für alle
für alle  und
und 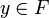 .
.- Ein lokalkonvexer Raum ist genau dann nuklear, wenn jede stetige Bilinearform
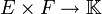 für jeden lokalkonvexen Raum F nuklear ist.
für jeden lokalkonvexen Raum F nuklear ist.
- Ein lokalkonvexer Raum ist genau dann nuklear, wenn jede stetige Bilinearform
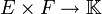 für jeden Banachraum F nuklear ist.
für jeden Banachraum F nuklear ist.
Diese Charakterisierung nuklearer Räume nennt man auch die abstrakte Form des Satzes vom Kern.
Summierbarkeit
Ist
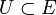 eine absolutkonvexe Nullumgebung, so sei pU das zugehörige Minkowski-Funktional.
eine absolutkonvexe Nullumgebung, so sei pU das zugehörige Minkowski-Funktional. 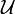 sei eine Nullumgebungsbasis aus absolutkonvexen Mengen. Sei
sei eine Nullumgebungsbasis aus absolutkonvexen Mengen. Sei 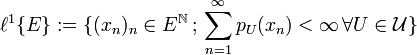 mit den Halbnormen
mit den Halbnormen 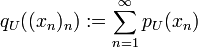 versehen. Der dadurch entstehende lokalkonvexe Raum heißt in naheliegender Weise Raum der absoluten Cauchy-Reihen. In dieser Definition wird nicht verlangt, dass die Reihe
versehen. Der dadurch entstehende lokalkonvexe Raum heißt in naheliegender Weise Raum der absoluten Cauchy-Reihen. In dieser Definition wird nicht verlangt, dass die Reihe 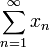 in E konvergiert.
in E konvergiert.Weiter betrachten wir den Raum
![\ell^1[E] := \{ (x_n)_n \in E^{\mathbb N}\,;\, (f(x_n))_n\in\ell^1\,\,\forall f\in E'\}](/pictures/dewiki/97/a9202359a568e2dc874fadc475c67928.png) mit den Halbnormen
mit den Halbnormen 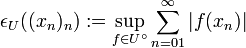 , wobei
, wobei  wie oben die Polare von U bezeichnet und U die Nullumgebungsbasis
wie oben die Polare von U bezeichnet und U die Nullumgebungsbasis 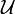 durchläuft. Dieser lokalkonvexe Raum heißt Raum der unbedingten Cauchy-Reihen, denn aus dem riemannschen bzw. steinitzschen Umordnungssatz folgt leicht, dass mit (xn)n auch jede permutierte Folge (xσ(n))n in
durchläuft. Dieser lokalkonvexe Raum heißt Raum der unbedingten Cauchy-Reihen, denn aus dem riemannschen bzw. steinitzschen Umordnungssatz folgt leicht, dass mit (xn)n auch jede permutierte Folge (xσ(n))n in ![\ell^1[E]](/pictures/dewiki/54/68b3c97d7d34757ca9775c63202638d3.png) liegt.
liegt.Sowohl
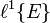 als auch
als auch ![\ell^1[E]](/pictures/dewiki/54/68b3c97d7d34757ca9775c63202638d3.png) sind unabhängig von der speziellen Wahl der Nullumgebungsbasis. Die nuklearen Räume erweisen sich nun als diejenigen, in denen absolute Cauchy-Reihen und unbedingte Cauchy-Reihen zusammenfallen:
sind unabhängig von der speziellen Wahl der Nullumgebungsbasis. Die nuklearen Räume erweisen sich nun als diejenigen, in denen absolute Cauchy-Reihen und unbedingte Cauchy-Reihen zusammenfallen:- Ein lokalkonvexer Raum ist genau dann nuklear, wenn
![\ell^1\{E\} = \ell^1[E]](/pictures/dewiki/102/fa1cc0256b1ad48333c030b35ea7f0b3.png) als Mengen und als topologische Räume.
als Mengen und als topologische Räume.
Satz von Kōmura-Kōmura
Der hier vorgestellte auf T. Kōmura und Y. Kōmura zurückgehende Satz zeigt, dass der in den Beispielen angegebene Folgenraum s der schnell fallenden Folgen ein Generator aller nuklearen Räume ist.
- Ein lokalkonvexer Raum E ist genau dann nuklear, wenn es eine Menge I gibt, so dass E isomorph zu einem Unterraum von sI ist.
Beispiele
Normierte Räume
Unter den normierten Räumen sind genau die endlich-dimensionalen nuklear.
Schnell fallende Folgen
Sei
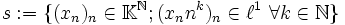 mit den Halbnormen
mit den Halbnormen 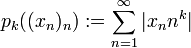 . Dieser lokalkonvexe Raum heißt Raum der schnell fallenden Folgen und ist nach obigem Satz von Kōmura-Kōmura ein Prototyp eines nuklearen Raums.
. Dieser lokalkonvexe Raum heißt Raum der schnell fallenden Folgen und ist nach obigem Satz von Kōmura-Kōmura ein Prototyp eines nuklearen Raums.Differenzierbare Funktionen
Wichtige Beispiele sind auch Räume differenzierbarer Funktionen. Sei
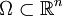 offen und
offen und 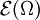 der Raum der beliebig oft differenzierbaren Funktionen
der Raum der beliebig oft differenzierbaren Funktionen 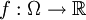 mit den Halbnormen
mit den Halbnormen  , wobei
, wobei 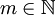 und
und 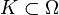 kompakt ist. Dabei wurde für
kompakt ist. Dabei wurde für  die Multiindex-Schreibweise verwendet. Dann ist
die Multiindex-Schreibweise verwendet. Dann ist 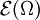 ein nuklearer Raum.
ein nuklearer Raum.Testfunktionen
Sei
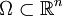 offen und
offen und 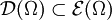 der Unterraum der beliebig oft differenzierbaren Funktionen mit einem kompakten Träger in Ω. Für kompaktes
der Unterraum der beliebig oft differenzierbaren Funktionen mit einem kompakten Träger in Ω. Für kompaktes 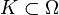 sei
sei 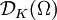 der Raum der Funktionen mit Träger in K mit der von
der Raum der Funktionen mit Träger in K mit der von 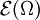 induzierten Teilraumtopologie. Dann gibt es eine feinste lokalkonvexe Topologie auf
induzierten Teilraumtopologie. Dann gibt es eine feinste lokalkonvexe Topologie auf 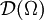 , die alle Einbettungen
, die alle Einbettungen 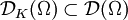 stetig macht.
stetig macht. 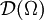 mit dieser Topologie heiß der Raum der Testfunktionen und spielt eine wichtige Rolle in der Distributionstheorie.
mit dieser Topologie heiß der Raum der Testfunktionen und spielt eine wichtige Rolle in der Distributionstheorie. 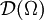 ist ein Beispiel für einen nicht-metrisierbaren nuklearen Raum.
ist ein Beispiel für einen nicht-metrisierbaren nuklearen Raum.Schnell fallende Funktionen
Sei
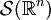 der Raum aller Funktionen
der Raum aller Funktionen  , für die alle Suprema
, für die alle Suprema 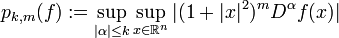 endlich sind. Dabei wurde wieder von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum
endlich sind. Dabei wurde wieder von der Multiindex-Schreibweise Gebrauch gemacht. Der Raum 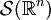 mit den Halbnormen
mit den Halbnormen 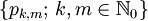 heißt Raum der schnell fallenden Funktionen und ist ebenfalls nuklear.
heißt Raum der schnell fallenden Funktionen und ist ebenfalls nuklear.Holomorphe Funktionen
Sei
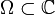 offen und
offen und 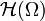 der Raum aller holomorphen Funktionen
der Raum aller holomorphen Funktionen 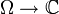 . Dann ist
. Dann ist 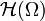 mit den Halbnormen pK: = pK,0, wobei
mit den Halbnormen pK: = pK,0, wobei 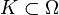 kompakt ist, ein nuklearer Raum.
kompakt ist, ein nuklearer Raum.Permanenzeigenschaften
Nukleare Räume haben sehr gute Permanenzeigenschaften. Unterräume, Faktorräume nach abgeschlossenen Unterräumen, beliebige Produkte, abzählbare direkte Summen, Tensorprodukte und Vervollständigungen nuklearer Räume sind wieder nuklear.
Eigenschaften
- Nukleare Räume besitzen die Approximationseigenschaft.
- In metrisierbaren, nuklearen gilt die Verallgemeinerung des Steinitzschen Umordnungssatzes, wie im Artikel über die Umordnung von Reihen ausgeführt ist.
- Vollständige nukleare Räume sind Schwartz-Räume.
- Nukleare Fréchet-Räume sind Montel-Räume.
- Der starke Dualraum eines nuklearen Raums ist ein tonnelierter Raum.
- In quasivollständigen nuklearen Räumen gilt der Satz von Bolzano-Weierstraß, d.h. eine Menge ist genau dann kompakt, wenn sie abgeschlossen und beschränkt ist.
- Quasivollständige nukleare Räume sind halbreflexiv. Daher sind quasivollständige, quasitonnelierte, nukleare Räume reflexiv.
Literatur
- A Grothendieck: Résumé des résultats essentiels dans la théorie des produits tensoriels topologiques et des espaces nucléaires, Ann. Inst. Fourier 4 (1954), 73-112
- K. Floret, J. Wloka: Einführung in die Theorie der lokalkonvexen Räume, Lecture Notes in Mathematics 56, 1968
- H. H. Schaefer: Topological Vector Spaces, Springer, 1971 ISBN 0-387-98726-6
- H. Jarchow: Locally Convex Spaces, Teubner, Stuttgart 1981 ISBN 3-519-02224-9
- R. Meise, D. Vogt: Einführung in die Funktionalanalysis, Vieweg, 1992 ISBN 3-528-07262-8
- Ein lokalkonvexer Raum ist genau dann nuklear, wenn es zu jeder stetigen Halbnorm p eine weitere stetige Halbnorm
Wikimedia Foundation.
