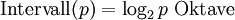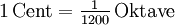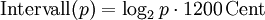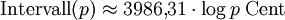Cent (Intervall)

Einheit
Norm	Hilfsmaßeinheit
Einheitenname	Cent
Einheitenzeichen	C, Cent
Beschriebene Größe(n)	musikalisches Intervall
Größensymbol(e)	Δ
Dimensionsname	1 (dimensionslos)
In SI-Einheiten

Das Cent (von lat. centum „hundert“) dient als logarithmische Maßeinheit für musikalische Intervalle. Der Name kommt daher, dass ein gleichstufiger Halbton in 100 Schritte geteilt wird. Da eine Oktave zwölf Halbtöne umfasst, entspricht sie 1200 Cent. Die Einheit Cent ist in DIN 13320 genormt (siehe unten) und bezeichnet eine relative Frequenzänderung von 1 Cent ≈ 0,57779 ‰ (Promille).

Mittels Angaben in Cent können verschiedene Tonsysteme und Stimmungen bequem verglichen werden. Der Tonhöhenvergleich mittels dieser Einheit hat den Vorteil, dass er dem additiven Intervall-Empfinden des Gehörs entspricht, das schon Aristoxenos seiner Tonsystemtheorie zugrunde legte. Er ist damit praxisnäher als eine Beschreibung in unanschaulichen Saitenlängen- oder Frequenz-Verhältnissen.

Entstehung

Die Bezeichnung Cent wurde 1875 von Alexander John Ellis (1814–1890) im Anhang zu seiner Übersetzung von Hermann von Helmholtz' „Lehre von den Tonempfindungen“ als Einheit zum Größenvergleich von Intervallen vorgeschlagen.

Die Cent-Einheit ist so gewählt, dass wahrnehmbare Frequenzunterschiede hinreichend genau als ganzzahlige Vielfache von Cents ausgedrückt werden können. Grob kann angenommen werden, dass der kleinste erkennbare Frequenzunterschied für Sinustöne beim Menschen bei Frequenzen ab 1000 Hz bei etwa drei bis sechs Cent liegt. Geringere Intervallunterschiede werden beim Nacheinander-Erklingen der Töne nicht mehr erkannt. Bei gleichzeitigem Erklingen sind durch Schwebungseffekte noch wesentlich geringere Unterschiede hörbar. Bei größeren Tonabständen lassen sich Intervallgrößen durch Schwebungen der harmonischen Obertöne sehr genau bestimmen, die in musikalisch verwendeten Tönen meistens vorhanden sind. Bei tiefen Sinustönen mit geringer Lautstärke steigt hingegen die Unterscheidungsschwelle auf über 100 Cent, also einem Halbton.

Umrechnung von Proportionen in Cent

Die Berechnung geht von der Proportion von Intervallen aus, die als Frequenzverhältnis oder Saitenlängenverhältnis gegeben ist. Zur Berechnung eines beliebigen Intervalls mit der Proportion p benutzt man seit etwa 1650 folgende logarithmische Gleichung, die für Intervalle definiert ist:

$\mathrm{Intervall}(p)= \log_2{p} \;\mathrm{Oktave} \,$

Diese Gleichung übersetzt die multiplikativen akustischen Proportionen in die additiven musikalischen Intervalle (Beispiel unten). Nach Einsetzung der Definitionsgleichung

$1\,\mathrm{Cent}=\tfrac{1}{1200}\,\mathrm{Oktave} \,$

ergibt sich die Umrechnung von Proportion in Cent:

$\mathrm{Intervall}(p)= \log_2{p} \cdot 1200\,\mathrm{Cent} \,$

Nach Umrechnung des Zweier-Logarithmus in einen Zehner-Logarithmus über die Gleichung log₂ x = log x / log 2 entsteht eine für Taschenrechner bequem handhabbare Näherungsgleichung:

$\mathrm{Intervall}(p)\approx 3986{,}31 \cdot \log{p} \;\mathrm{Cent} \,$

Beispiel: Dreiklangsintervalle

Ein Dreiklang besteht aus einer reinen großen Terz und einer reinen kleinen Terz, die sich zur reinen Quinte summieren („rein“ ist hier nicht im Unterschied zu „vermindert“ und „übermäßig“ gemeint, sondern in der Bedeutung „nicht temperiert“, mit dem genauen Frequenzverhältnis 2:3, so dass auch der Begriff „reine" Terz sinnvoll ist; siehe auch Reines Intervall).

In der meistens ausreichenden Näherung mit ganzen Zahlen von Cents ergibt sich:

Intervall mit Proportion p	Intervall Δ in Cent
reine kleine Terz 6/5	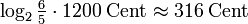$\log_2{\tfrac{6}{5}}\cdot 1200 \;\mathrm{Cent} \approx 316\;\mathrm{Cent}$
reine große Terz 5/4	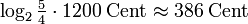$\log_2{\tfrac{5}{4}}\cdot 1200\;\mathrm{Cent} \approx 386\;\mathrm{Cent}$
reine Quinte 3/2	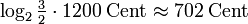$\log_2{\tfrac{3}{2}}\cdot 1200 \;\mathrm{Cent} \approx 702\;\mathrm{Cent}$

Die Additionsgleichung der Dreiklangsintervalle entspricht der Multiplikation der Proportionen in Brüchen ausgedrückt:

reine große Terz + reine kleine Terz = reine Quinte

$386\;\mathrm{Cent} + 316\;\mathrm{Cent} = 702\;\mathrm{Cent} \,$

$\tfrac{5}{4} \cdot \tfrac{6}{5} = \tfrac{3}{2} \,$

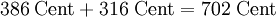
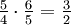
Umrechnung von Cent in Proportionen

Die umgekehrte Umrechnung von Cent in Proportion wird seltener benötigt. Zur Berechnung der Proportion eines beliebigen Intervalls Δ benützt man die für Intervalle definierte Umkehrfunktion:

$\mathrm{Proportion}(\Delta)= 2^\frac{\Delta}{\mathrm{Oktave}} \,$.

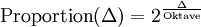Mit Hilfe der obigen Definition ergibt sich:

$\mathrm{Proportion}(\Delta)=2^\frac{\Delta}{1200\,\mathrm{Cent}} \,$.

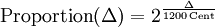Mit bekannten Rechenregeln für Potenzen ergibt sich folgende Näherung für den Taschenrechner:

$\mathrm{Proportion}(\Delta)\approx 1{,}00057779^\frac{\Delta}{\mathrm{Cent}} \,$.

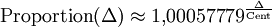Bei den Dreiklangsintervallen erhält man folgende Umrechnung:

Intervall Δ in Cent	Proportion p	Intervall
316 Cent	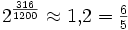$2^{\frac{316}{1200}} \approx 1{,}2 = \tfrac{6}{5}$	reine kleine Terz
386 Cent	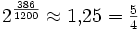$2^{\frac{386}{1200}} \approx 1{,}25 = \tfrac{5}{4}$	reine große Terz
702 Cent	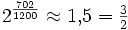$2^{\frac{702}{1200}} \approx 1{,}5 = \tfrac{3}{2}$	reine Quinte

Berechnung von Frequenzen

Der oben genannte Faktor $\sqrt[1200]{2} \approx 1{,}00057779$ ist die Proportion (das Frequenzverhältnis) eines Tonunterschiedes von einem Cent. Die Frequenzberechnung erfolgt daher mit dieser Zahl als Basis und dem Intervall in Cent im Exponenten. Beispiele einiger praktisch als Stimmton a¹ verwendeter Frequenzen, von 440 Hz ausgehend:

• Erhöhung um 1 Cent: $440{,}0\,\mathrm{Hz} \cdot 1{,}00057779^{1} = 440{,}2545\,\mathrm{Hz}$
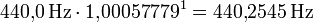
• Erhöhung um 4 Cent: $440{,}0\,\mathrm{Hz} \cdot 1{,}00057779^{4} = 441{,}0164\,\mathrm{Hz}$
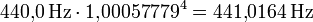
• Erhöhung um 12 Cent: $440{,}0\,\mathrm{Hz} \cdot 1{,}00057779^{12} = 443{,}0624\,\mathrm{Hz}$
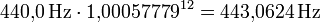
• Vertiefung um 19 Cent: $440{,}0\,\mathrm{Hz} \cdot 1{,}00057779^{-19} = 435{,}1954\,\mathrm{Hz}$
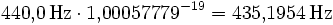
• Vertiefung um 101 Cent: $440{,}0\,\mathrm{Hz} \cdot 1{,}00057779^{-101} = 415{,}0630\,\mathrm{Hz}$

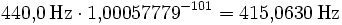
DIN-Norm

Nach DIN 13320 „Akustik; Spektren und Übertragungskurven; Begriffe, Darstellung“ bezeichnet Cent ein Frequenzmaßintervall, dessen Frequenzverhältnis 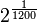$2^{\frac{1}{1200}}$ beträgt. Das Cent kann wie eine Einheit benutzt werden; somit kann das Frequenzmaßintervall der Frequenzen f₁ und f₂ (f₂ > f₁) als 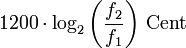$1200 \cdot \log_2 \left( \frac{f_2}{f_1} \right)\,\mathrm{Cent}$ bezeichnet werden.

Siehe auch

• Millioktave, Savart

Literatur

• Helmholtz, Hermann: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik, 1875
• John R. Pierce: Klang. Musik mit den Ohren der Physik, Spektrum, ISBN 3-8274-0544-0

Weblinks

• Intervall Umrechnung: Frequenzverhältnis nach Cent und Cent nach Frequenz (ratio)
• Umrechnung Cent in Frequenzverhältnis Ratio und zurück in Excel - xls
• Zusammenstellung logarithmischer Maßeinheiten zu Intervallgrößen - engl.
• Hermann Helmholtz: Die Lehre von den Tonempfindungen als physiologische Grundlage für die Theorie der Musik
• Das Centmaß für Intervalle