Formelsammlung elementare Algebra

$\sqrt[n]{x}$

Dieser Artikel ist eine Formelsammlung zum Thema Elementare Algebra. Es werden mathematische Symbole verwendet, die im Artikel Mathematische Symbole erläutert werden.

Grundrechenarten

Siehe dazu: Formelsammlung Grundrechenarten.

Arithmetische Notation

Es gilt: Punkt- vor Strichrechnung. Das heißt, die Rechenoperationen der zweiten Stufe (Multiplikation und Division) binden stärker als die der ersten Stufe (Addition und Subtraktion). Das ist kein mathematisches Gesetz sondern eine weltweit verbreitete Konvention, um Klammern zu sparen und in den meisten Industrieländern genormt.

$a + ( b \cdot c ) + d = a + b \cdot c + d$

$( a \cdot b ) + ( c \cdot d ) = a \cdot b + c \cdot d$

$( a + b ) \cdot ( c + d ) \neq a + b \cdot c + d$

Bei Verwendung der Polnischen Notation bzw. der Umgekehrten Polnischen Notation bedarf es keiner Klammerung.

Darüber hinaus binden die Rechenoperationen der dritten Stufe (Radizieren und Potenzieren) stärker als die der zweiten Stufe. Das ist besonders bei Notationen mit eingeschränkten typografischen Möglichkeiten (z.B. ein "^" statt Hochstellen bei reinem ASCII) wichtig:

a * b ^ c = a * (b ^ c)

Axiome

• Assoziativgesetz

  $a \cdot \left( b \cdot c \right) = \left( a \cdot b \right) \cdot c$

  $a + \left( b + c \right) = \left( a + b \right) + c$

• Kommutativgesetz (Vertauschungsgesetz)

  $a + b = b + a \,$

  $a \cdot b = b \cdot a$

• Distributivgesetz

  $a \cdot \left( b + c \right) = a \cdot b + a \cdot c$ (linksdistributiv)

  $\left( a + b \right) \cdot c = a \cdot c + b \cdot c$ (rechtsdistributiv)

Prozentrechnung

Grundgleichung

$\frac{\text{Prozentwert}}{\text{Grundwert}} = \frac{\text{Prozentsatz}}{100}$

Mit

Prozentwert = Pw

Grundwert = Gw

Prozentsatz = Ps

ergibt sich

$\frac{Pw}{Gw} = \frac{Ps}{100}$

bzw.

$Pw \cdot 100 = Gw \cdot Ps$

Durch Umformungen erhält man

$Pw = Gw \cdot \frac{Ps}{100}$

$Gw = Pw \cdot \frac{100}{Ps}$

$Ps = 100 \cdot \frac{Pw}{Gw}$

Kontrollrechnung:

$\frac{Gw \cdot Ps}{Pw} = 100$

Mit

$p = \frac{Ps}{100}$

gilt

$\frac{Pw}{Gw} = p$

Vermehrter Grundwert

$\!\,Gw^* = Gw \cdot \frac{100 + p}{100}$

Verminderter Grundwert

$\!\,Gw^* = Gw \cdot \frac{100 - p}{100}$

Prozentsätze häufig benutzter Anteile

Anteil am Grundwert	$\frac{1}{100}$	$\frac{1}{50}$	$\frac{1}{40}$	$\frac{1}{25}$	$\frac{1}{20}$	$\frac{1}{16}$	$\frac{1}{15}$
Prozentsatz	1%	2%	2,5%	4%	5%	6,25%	≈6,67%
Anteil am Grundwert	$\frac{1}{12}$	$\frac{1}{11}$	$\frac{1}{10}$	$\frac{1}{9}$	$\frac{1}{8}$	$\frac{1}{7}$	$\frac{1}{6}$
Prozentsatz	≈8,33%	≈9,09%	10%	≈11,11%	12,5%	≈14,29%	≈16,67%
Anteil am Grundwert	$\frac{1}{5}$	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{3}{8}$	$\frac{1}{2}$	$\frac{2}{3}$	$\frac{3}{4}$
Prozentsatz	20%	25%	≈33,33%	37,5%	50%	≈66,67%	75%

Elementare Funktionen

Potenz

• Definition Potenzen

  $a^n = a \cdot a \cdot \dots \cdot a =\prod\limits^n_{i=1} a$ (n Faktoren)

  Formal (induktiv):

  $a^n=\begin{cases} 1 & \mathrm{f\ddot ur} \quad n=0 \\ a\cdot a^{n-1} & \mathrm{f\ddot ur} \quad n \ge 1 \end{cases}$

• Begriffe zur Potenz

  $\,a^n$ (das Ergebnis der Rechnung) ist die Potenz

  $\,a$ ist die Basis

  $\,n$ ist der Exponent

• Potenzen mit gleicher Basis

  $a^x \cdot a^y = a^{x+y}$

  $\frac{a^x}{a^y} = a^{x-y}$

• Potenzieren einer Potenz

  $({a^x})^y = a^{x \cdot y}$

• Potenzen mit gleichem Exponenten

  $a^x \cdot b^x = (a \cdot b)^x$

  $\frac{a^x}{b^x} = \left( \frac{a}{b} \right)^x$

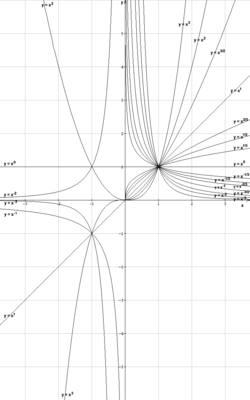
Potenzfunktion mit ganzzahligem Exponenten

Graphen einiger Potenzfunktionen

$f(x)=x^n \qquad \text{mit} \qquad n \in \Z$

1. n positiv und gerade ($\!\,n = 2m; m \in \N^{+}$)

$f(x) = x^{2m} \qquad \text{mit} \qquad D_f = \R$

Wertebereich

$\!\,W_f = [0; + \infty[$

Nullstellen

$\!\,x_0 = 0$

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(-1;1), (0;0), (1;1)$

2. n positiv und ungerade ($\!\,n = 2m + 1; m \in \N^{+}$)

$\!\,f(x)=x^{2m + 1} \qquad \text{mit} \qquad D_f = \R$

Wertebereich

$\!\,W_f = \R$

Nullstellen

$\!\,x_0 = 0$

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(-1;-1), (0;0), (1;1)$

3. n negativ und gerade ($\!\,n = -2m; m \in \N^{+}$)

$\!\,f(x)=x^{-2m} \qquad \text{mit} \qquad D_f = \R \setminus {0}$

Wertebereich

$\!\,W_f = ]0; + \infty[$

Nullstellen

Diese Funktionen besitzen keine Nullstellen!

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(-1;1), (1;1)$

4. n negativ und ungerade ($\!\,n = -(2m-1); m \in \N^{+}$)

$\!\,f(x)=x^{-(2m-1)} \qquad \text{mit} \qquad D_f = \R \setminus {0}$

Wertebereich

$\!\,W_f = \R \setminus {0}$

Nullstellen

Diese Funktionen besitzen keine Nullstellen!

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(-1;-1), (1;1)$

Potenzfunktion mit gebrochenen Exponenten (Wurzelfunktion)

$\!\,f(x)=x^n \qquad \text{mit} \qquad n = \frac{p}{q} \qquad (p,q \in \N^{+}, p \ne q)$

Definitionsbereich

$\!\,D_f = [0, + \infty[$

Wertebereich

$\!\,W_f = [0, + \infty[$

Nullstellen

$\!\,x_0 = 0$

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(0;0), (1;1)$

Wurzeln

• Begriffe zu Wurzeln

  $x = \sqrt[n]{a}$

  $\sqrt[n]{a}$ (Das Ergebnis der Rechnung) ist die Wurzel oder Radix.

  n ist der Wurzelexponent

  a ist der Radikand

• Definition Wurzel

  $x^n = a \Leftrightarrow x = \sqrt[n]{a} \qquad \left(a \in \mathbb{R},a \geq 0, n \in \mathbb{N^+}\right)$

• Negativer Radikand und ungerader Exponent

  $\sqrt[n]{-a}=-\sqrt[n]{a}\qquad \left(a \in \mathbb{R}, n \in \mathbb{N^+}, n=2u-1,u \in \mathbb{N^+}\right)$

Für $n,m \in \mathbb{N};\,n \geq 2;\, a \in \mathbb{R};\, a,\,b>0$ gelten folgende Regeln

• $\sqrt[n]{a} = a^\frac{1}{n}$
• $\sqrt[n]{a ^m} = ({\sqrt[n]{a}}) ^m = a^\frac{m}{n}$
• $\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}$
• ${{ \sqrt[n]{a}} \over {\sqrt[n]{b}}} = \sqrt[n]{a \over b}$
• $\sqrt[n]{{\sqrt[m]{a}}} = \sqrt[n \cdot m]{a}$
• $\sqrt[n]{a} \cdot \sqrt[m]{a} = \sqrt[n \cdot m]{a^{n+m}}$
• $\frac{\sqrt[n]{a}}{\sqrt[m]{a}} = \sqrt[n \cdot m]{a^{m-n}}$

und die Regeln können auf $n,m\in\mathbb{R}$ erweitert werden.

Logarithmus

• Definition des Logarithmus zur Basis b

  $x = \log_b a \Leftrightarrow a = b^x$

• Logarithmusgesetze
  1. $\log_x ( a \cdot b) = \log_x a + \log_x b$
  2. $\log_x \left( \frac{a}{b} \right) = \log_x a - \log_x b$
  3. $\log_x \left( a^b \right) = b \cdot \log_x a$
• Basiswechsel
  1. $\log_b a = c \Longleftrightarrow c = \frac{\log_x a}{\log_x b}$

Logarithmusfunktion

$f(x) = \log_a x \qquad \text{mit} \qquad a \in \R, a > 0, a \ne 1$

Definitionsbereich

$\!\,D_f = ]0, + \infty[$

Wertebereich

$\!\,W_f = \R$

Nullstellen

$\!\,x_0 = 1$

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(1;0)$

Spezialfälle

$\!\,f(x) = \log_{10} x = \lg x$

$\!\,f(x) = \log_e x = \ln x$

$\!\,f(x) = \log_2 x = \operatorname{lb} x$

Exponentialfunktion

$\!\,f(x)=a^x \qquad \text{mit} \qquad a \in \R, a > 0, a \ne 1$

Definitionsbereich

$\!\,D_f = \R$

Wertebereich

$\!\,W_f = ]0, + \infty[$

Nullstellen

Diese Funktionen besitzen keine Nullstellen!

Gemeinsame Punkte aller Funktionsgraphen

$\!\,(0;1)$

Spezialfall

$\!\,f(x) = e^x$

Betragsfunktion, Signum, Gaußklammer

Betrag:

$|x|:= \begin{cases} \;\;\,x & \mathrm{f\ddot ur} \quad x>0 \\ \;\;\,0 & \mathrm{f\ddot ur} \quad x=0 \\ -x & \mathrm{f\ddot ur} \quad x<0 \\ \end{cases}$

Signum:

$\sgn(x):= \begin{cases} \;\;\,1 & \mathrm{f\ddot ur} \quad x>0 \\ \;\;\,0 & \mathrm{f\ddot ur} \quad x=0 \\ -1 & \mathrm{f\ddot ur} \quad x<0 \\ \end{cases}$

Das Signum einer komplexen Zahl ≠ 0 ist gleich die Zahl geteilt durch ihren Betrag, also sign(z)=z/|z|.

Also gilt: $x = \sgn(x) \cdot |x|$

Die Gaußklammer einer (reellen) Zahl ist die größte ganze Zahl, die nicht größer als die Zahl selbst ist.

Termumformungen

8 − (2 − a + b)

Hier ist die „Minusklammer“ zu beachten. Minusklammer heißt, dass vor der Klammer ein Minus (-) steht. Somit müssen alle Werte in der Klammer mit (−1) multipliziert werden.

$\begin{array}{llccc} =& 8 &+ (2\cdot(-1) &- a\cdot(-1) &+ b\cdot(-1)) \\ =& 8 &- 2 &+ a &- b \\ =& 6 &&+ a &- b \end{array}$

Generell dürfen bei einer Gleichung folgende Termumformungen durchgeführt werden

• Addition (und folglich auch Subtraktion) derselben Zahl oder Variablen auf beiden Seiten des Gleichheitszeichens
• Multiplikation (und folglich auch Division) derselben Zahl ungleich Null auf beiden Seiten des Gleichheitszeichens

sowie

• Klammern auflösen
• Seiten vertauschen
• Summanden vertauschen

jeweils auf einer Seite der Gleichung.

Beispiel:

$\begin{array}{lll} 3(2x-1) + 2 & = x & \| \mbox{Klammer auflösen (Distributivgesetz)}\\ 6x - 3 + 2 & = x & \| \mbox{Zusammenfassen}\\ 6x - 1 & = x & \| - 6x\\ - 1 & = -5x & \| :(-5)\\ \frac{1}{5} & = x & \end{array}$

Grundlegende Funktionen

Definition

In der Mathematik ist eine Funktion oder Abbildung eine Beziehung zwischen zwei Mengen, die jedem Element der einen Menge (Eingangsgröße, Funktionsargument, unabhängige Variable, x-Wert) ein Element der anderen Menge (Ausgangsgröße, Funktionswert, abhängige Variable, y-Wert) zuordnet:

$f\colon D\to Z$ oder

$f\colon x\mapsto y$

Gerade Funktion

$\!\,f(x) = f(-x) \qquad \mathrm{f\ddot ur\ jedes} \quad x \in D_f$

Der Graph liegt somit symmetrisch zur y-Achse!

Ungerade Funktion

$\!\,f(x) = -f(-x) \qquad \mathrm{f\ddot ur\ jedes} \quad x \in D_f$

Der Graph liegt somit zentralsymmetrisch zum Koordinatenursprung!

Lineare Funktion

Geraden - Graphen der Linearen Funktion

$\!\,f(x) = m x + n \qquad \text{mit} \qquad m \ne 0$ und $D_f = \R$

Wertebereich

$\!\,W_f = \R$

Nullstellen

$\!\,x_0=-\frac{n}{m}$

Schnittpunkte mit der y-Achse

$\!\,S(0;n)$

Steigung

$\!\,m=\tan{\alpha}=\frac{f(x_2)-f(x_1)}{x_2-x_1}$

$\!\,\alpha \rightarrow$ Schnittwinkel des Graphen mit der x-Achse

$\!\,m > 0 \rightarrow$ steigende Gerade

$\!\,m < 0 \rightarrow$ fallende Gerade

Lineares Gleichungssystem

Ein System aus $\!\,m$ linearen Gleichungen mit $\!\,n$ Variablen $\!\,x_1, x_2, x_3, \dots, x_n$ wird lineares Gleichungssystem genannt.

Jedes derartige Gleichungssystem lässt sich in folgender Form darstellen:

$\begin{matrix} a_{11}x_1 & + & a_{12}x_2 & + & a_{13}x_3 & + & \dots & + & a_{1n}x_n & = b_1\\ a_{21}x_1 & + & a_{22}x_2 & + & a_{23}x_3 & + & \dots & + & a_{2n}x_n & = b_2\\ a_{31}x_1 & + & a_{32}x_2 & + & a_{33}x_3 & + & \dots & + & a_{3n}x_n & = b_3\\ \vdots & & & & & & & & & \vdots\\ a_{m1}x_1 & + & a_{m2}x_2 & + & a_{m3}x_3 & + & \dots & + & a_{mn}x_n & = b_m\\ \end{matrix}$

Homogenes und Inhomogenes System

Ein Lineares Gleichungssystem, bei dem alle Konstanten $\!\,b_i$ (Absolutglieder) den Wert $\!\,0$ haben, heißt homogen.

Sind nicht alle Absolutglieder gleich $\!\,0$, so wird das System inhomogen genannt.

Gleichsetzungsverfahren

Hierbei werden die Gleichungen, jede für sich, so umgeformt, dass dieselbe Variable in jeder Gleichung allein auf einer Seite steht. Zwei der auf der anderen Seite erhaltenen Ausdrücke werden dann gleichgesetzt.

Additionsverfahren

Wie der Name schon im Ansatz verrät, werden mit Hilfe des Additionsverfahren Gleichungen addiert. Dies geschieht in der Regel so, dass eine oder gleich mehrere Variablen in den Gleichungen eliminiert werden:

$\begin{matrix} (1) & 5x & + & 3y & = & 5\\ (2) & 3x & + & y & = & -1 \end{matrix}$

Dazu muss eine der beiden Gleichungen so umgeformt werden, dass bei einer Addition der beiden Gleichungen eine Variable verschwindet. In diesem Beispiel multiplizieren wir dazu Gleichung (2) auf beiden Seiten mit $\!\,-3$:

$\!\,(2) \quad 3x + y = -1 | \cdot (-3)$

Dadurch erhalten wir ein gleichwertiges Gleichungssystem, in dem der Term $\!\,-3y$ vorkommt:

$\begin{matrix} (1) & 5x & + & 3y & = & 5 \\ (2') & -9x & - & 3y & = & 3 \end{matrix}$

Nun werden beide Gleichungen des Systems addiert und somit in einer Gleichung zusammengefasst:

$\begin{matrix} (5x + 3y) & + & (-9x - 3y) & = & 5 + 3 \\ 5x - 9x & + & 3y - 3y & = & 8 \\ - 4x & + & 0y & = & 8 \\ -4x & & & = & 8 \end{matrix}$

Anschließend wird nach der verbliebenen Variablen $\!\,x$ aufgelöst:

$\begin{matrix} -4x & = & 8 & | \div (-4) \\ x & = & -2& \end{matrix}$

Damit ist der Wert der ersten Variable bekannt. Diesen Wert ($\!\,x = -2$) setzen wir in Gleichung (1) ein, um den Wert der zweiten Variable zu berechnen:

$\begin{matrix} 5 \cdot (-2) & + & 3y & = & 5 \\ -10 & + & 3y & = & 5 &|& + & 10 \\ & & 3y & = & 15 &|& \div & 3 \\ & & y & = & 5 \end{matrix}$

Dadurch erhalten wir die Lösungsmenge: $\!\,\mathbb{L} = \{(-2\,|\,5)\}$.

Einsetzungsverfahren

Die Idee hinter dem Einsetzungsverfahren ist folgende: Man löst eine der Gleichungen nach einer Variablen auf und setzt diese Variable dann in die anderen Gleichungen ein. Dadurch wird eine Variable eliminiert.

Bei einem Gleichungssystem mit zwei Gleichungen und zwei Variablen geht man so vor:

1. Schritt 1: Auflösung einer Gleichung nach einer Variablen
2. Schritt 2: Einsetzen dieser Variablen in die anderen Gleichung
3. Schritt 3: Auflösen der im Schritt 2 erhaltenen Gleichung nach der enthaltenen Variablen
4. Schritt 4: Einsetzen der Lösung in die nach Schritt 1 umgeformten Gleichung

Gegeben ist folgendes Gleichungssystem:

$\begin{matrix} (1) & 12x & - & 5y & = & 29\\ (2) & 18x & + & 2y & = & 34 \end{matrix}$

Schritt 1:

Eine der beiden Gleichungen muss nach x oder y aufgelöst werden. In diesem Beispiel wird die 2. Gleichung nach y aufgelöst.

$\begin{matrix} (2) & 18x & + & 2y & = & 34 & |&-18x \\ (2) & & & 2y & = & 34 - 18x & |&:2 \\ (2) & & & y & = & 17 - 9x \end{matrix}$

Schritt 2:

Danach können wir in der ersten Gleichung das y durch den Term (17 − 9x) ersetzen und bekommen dann:

$\begin{matrix} (2 \text{ in } 1) & 12x & - & 5 \cdot (17 - 9x) & = & 29 \end{matrix}$

Schritt 3:

Diese Gleichung können wir nun nach x auflösen.

$\begin{matrix} 12x - 5 \cdot (17 - 9x) & = & 29 & |&\mathrm{Klammer aufl\ddot osen} \\ 12x - 85 + 45x & = & 29 & |&\text{zusammenfassen} \\ 57x - 85 & = & 29 & |&+85 \\ 57x & = & 114 & |&:57 \\ x & = & 2 \end{matrix}$

Schritt 4:

Die Lösung x = 2 wird in die umgestellte Gleichung (2) eingesetzt:

$\begin{matrix} x = 2 \text{ in (2) einsetzen:} & y & = & 17 - 9 \cdot 2\\ & y & = & -1 \end{matrix}$

Die Lösungsmenge ist somit: $\mathbb{L}=\{(2|-1)\}$.

Quadratische Gleichung

Allgemeine Form

Die Parabel - Graph der Quadratischen Funktionen

$\!\,f(x) = a x^2 + b x + c \qquad \text{mit} \qquad a \ne 0$ und $D_f = \R$

Wertebereich

$\!\,W_f = \left[\frac{4ac-b^2}{4a};+\infty\right) \qquad \mathrm{f\ddot ur}\quad a>0$

$\!\,W_f = \left(-\infty;\frac{4ac-b^2}{4a}\right] \qquad \mathrm{f\ddot ur}\quad a<0$

Nullstellen

$\!\,x_{1,2} = \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a}$

$\!\,b^2 - 4ac > 0 \rightarrow$ zwei verschiedene Nullstellen

$\!\,b^2 - 4ac = 0 \rightarrow$ genau eine (Doppel-)Nullstelle

$\!\,b^2 - 4ac < 0 \rightarrow$ keine reelle Nullstelle

Scheitelpunkte

$S\left(-\frac{p}{2}; -\frac{p^2}{4} + q\right)$

Normalform

$f(x) = x^2 + p x + q = 0 \qquad \text{mit} \left( p, q = \mathrm{const.} \right)$

Lösungen

$x_{1,2}= -\frac{p}{2} \pm \sqrt{{ \left( \frac{p}{2} \right) ^2} - q} = -\frac{p}{2} \pm \sqrt{\frac{p^2}{4} - q}$

$\left( \frac{p}{2} \right) ^2 - q > 0 \rightarrow$ zwei verschiedene Nullstellen

$\left( \frac{p}{2} \right) ^2 - q = 0 \rightarrow$ genau eine (Doppel-)Nullstelle

$\left( \frac{p}{2} \right) ^2 - q < 0 \rightarrow$ keine reelle Nullstelle

Zerlegung in Linearfaktoren

$x^2 + px + q = (x - x_1) \cdot (x - x_2) = 0$

Satzgruppe von Vieta

$p = -(x_1 + x_2) \qquad q = x_1 \cdot x_2$

Gleichung n-ten Grades

$\!\,P_n(x) = \sum_{i=0}^n a_ix^i = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \dots + a_2x^2 + a_1x^1 + a_0 = 0$

Lösungen (Nullstellen)

$\!\,x_1; x_2; x_3; \dots; x_n$

Zerlegung in Linearfaktoren

$\!\,P_n(x) = a_nx^n + a_{n-1}x^{n-1} + a_{n-2}x^{n-2} + \dots + a_2x^2 + a_1x^1 + a_0 = a_n(x-x_1)(x-x_2)\cdot \dots \cdot(x - x_n) = 0$

Lösungsverfahren

Ist $\!\,x_1$ eine durch Probieren gefundene Nullstelle, so kann $\!\,P_n(x)$ mittels Polynomdivision ohne Rest durch $\!\,(x-x_1)$ dividiert werden. Man erhält dadurch eine Gleichung (ein Polynom) ($\!\,n-1$)-ten Grades und es gilt: $\!\,P_n(x)=(x-x_1) \cdot P_{n-1}(x)$.

Fundamentalsatz der Algebra

Sei n der Grad (also die höchste vorkommende Potenz der Lösungsvariablen x) der Gleichung. Werden mehrfache Nullstellen entsprechend ihrer Vielfachheit gezählt, hat die Gleichung n (komplexe) Nullstellen.

Polynom n-ten Grades

Polynomdivision

Aufspaltung des Quotienten der Polynome $\;p(x)\in \mathrm{P}^n,\ q(x)\neq 0$ wie folgt:

$\frac{p(x)}{q(x)} = s(x) + \frac{r(x)}{q(x)}$

Damit $s(x) \neq 0$ ist und damit die Polynomdivision sinnvoll ist, muss für den Grad der Polynome gelten:

$\operatorname{Grad}\ p\ge\operatorname{Grad}\ q$.

Nun wird $\;p(x)$ schrittweise dividiert ($\;p_0(x) := p(x)$):

1. $\;s_i(x)$ wird so gewählt, dass $\;(s_i(x) q(x))_n = (p_i(x))_n$, dass also die Koeffizienten der höchsten in p vorkommenden Potenz gleich sind.
2. $\;p_{i+1}(x) := p_i(x) - q_i(x) s(x)$
3. Gilt $\operatorname{Grad}\ q(x) > \operatorname{Grad}\ p_{i+1}(x)$, so wird abgebrochen.
4. i wird inkrementiert und die Schleife erneut durchlaufen

Nach Abbruch gilt

• $s(x) = \sum_{k=1}^i s_k(x)$
• $\;r(x) = p_{i+1}(x)$

Mittelwerte

Mittelwert	Zwei Zahlen	Allgemein
Modus	Ausprägung mit höchster Häufigkeit
Median (Zentralwert)	Sofern $x_1, \ldots, x_n$ sortiert sind: $\bar{x}_\mathrm{med} =\begin{cases} x_{(\frac{n+1}{2})}, & n\text{ ungerade,}\\ \frac 12\left(x_{({\frac n2})} + x_{({\frac n2+1})}\right), & n \text{ gerade.} \end{cases}$
Arithmetisches Mittel	$\frac{a+b}2$	$\bar{x}_{\mathrm{arithm}} = \frac{1}{n} \sum_{i=1}^n{x_i} = \frac{x_1 + x_2 + \cdots + x_n}{n}$
Geometrisches Mittel	$\sqrt{ab}$	$\bar{x}_\mathrm{geom} = \sqrt[n]{\prod_{i=1}^n{x_i}} = \sqrt[n]{x_1 \cdot x_2 \cdot \ldots \cdot x_n}$
Harmonisches Mittel	$\frac2{\frac1a+\frac1b}$	$\bar{x}_\mathrm{harm} = \frac{n}{\sum\limits_{i=1}^n \frac{1}{x_i}} = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + \cdots + \frac{1}{x_n}}$
Quadratisches Mittel	$\sqrt{\frac{a^2+b^2}2}$	$\bar{x}_\mathrm{quadr} = \sqrt{\frac{1}{n}\sum_{i=1}^n{x_i^2}} = \sqrt {{x_1^2 + x_2^2 + \cdots + x_n^2} \over n}$

Komplexe Zahl

Definition

Eine komplexe Zahl ist eine Zahl vom Typ

$z=a+b\cdot \mathrm{i}\,$ mit $a,b \in \mathbb{R}$

a wird als Realteil und b als Imaginärteil bezeichnet.

$\mathrm{i}\,$ ist die imaginäre Einheit. Sie ist definiert als die Lösung der Gleichung

$\mathrm{i}^2 := -1 \,$

Potenzen der Einheit

i¹ = i

i² = − 1

$\mathrm{i}^3 = \mathrm{i}^2 \cdot \mathrm{i} = -1 \cdot \mathrm{i} = - \mathrm{i}$

$\mathrm{i}^4 = \mathrm{i}^2 \cdot \mathrm{i}^2 = -1 \cdot -1 = 1$

Allgemein:

i⁴ⁿ = 1

i^{4n + 1} = i

i^{4n + 2} = − 1

$\mathrm{i}^{4n+3} = \mathrm{i}^2 \cdot \mathrm{i} = -1 \cdot \mathrm{i} = - \mathrm{i}$

mit

$n \in \mathbb{Z}$

Komplexe Konjugation

Dreht man das Vorzeichen des Imaginärteils b einer komplexen Zahl $z = a+b\,\mathrm{i}$ um, so erhält man die zu z konjugiert komplexe Zahl $\bar z=a-b\,\mathrm{i}$ (manchmal auch z ^* geschrieben).

Grundrechenarten

Die Rechenoperationen Addition, Subtraktion, Multiplikation und Division können mit komplexen Zahlen , z.B. a + ib und x + iy genauso durchgeführt werden wie mit realen Zahlen, wenn man diese in Klammern setzt und als Besonderheit i² = -1 beachtet.

Addition

$\qquad(a + \mathrm ib) + (x + \mathrm iy) \,=\, (a + x) + \mathrm i(b + y)$

Subtraktion

$\qquad(a + \mathrm ib) - (x + \mathrm iy) \,=\, (a - x) + \mathrm i(b - y)$

Multiplikation

$\qquad(a + \mathrm ib)\cdot(x + \mathrm iy) \,=\, ax - by + \mathrm i(ay + bx)$

Division

$\qquad(a + \mathrm ib):(x + \mathrm iy) \,=\, \frac{ax + by}{x^2 + y^2} + \mathrm i\,\frac{bx - ay}{x^2 + y^2}\quad , \quad x^2+y^2 \, \not= \,0$

Diese Formel erhält man durch Erweiterung mit der konjugiert komplexen Zahl. Auch hier ist die Division durch Null nicht definiert.

Die Quadratwurzel errechnet sich

$\sqrt{a + \mathrm ib} \,=\, \left(\sqrt{\frac{a + \sqrt{a^2 + b^2}}{2}} + \mathrm i\frac{b}{\sqrt{2(a + \sqrt{a^2 + b^2})}}\right)$

Polarform und Exponentialform

Polarform

$z=r \cdot \cos (\varphi) + \mathrm{i} \cdot r \cdot \sin(\varphi)$

$z=r \cdot (\cos (\varphi) + \mathrm{i} \cdot \sin(\varphi))$

Exponentialform

$z=r \cdot e^{\mathrm{i}\varphi}$

r wird als Betrag und φ wird als Argument von z bezeichnet. (genauere Erklärung unter Komplexe Zahl)

Umrechnungsformeln

$r = |z| = \sqrt{a^2 + b^2}$   ;

für $z\neq 0$ wird das Argument wie folgt bestimmt:

$\varphi = \begin{cases}\arctan\frac{b}{a}&\mathrm{f\ddot ur}\ a>0\\ \arctan\frac ba+\pi&\mathrm{f\ddot ur}\ a<0,b\geq0\\ \arctan\frac ba-\pi&\mathrm{f\ddot ur}\ a<0,b<0\\ \pi/2&\mathrm{f\ddot ur}\ a=0,b>0\\ -\pi/2&\mathrm{f\ddot ur}\ a=0,b<0 \end{cases}$

oder

$\varphi =\begin{cases}\arccos\frac ar&\mathrm{f\ddot ur}\ b\geq0\\ \arccos\left(-\frac ar\right)-\pi&\mathrm{f\ddot ur}\ b<0 \end{cases}$

Sinus und Cosinus in komplexer Darstellung

$\sin x = {\left(e^{\mathrm{i}x} - e^{-\mathrm{i}x} \right) \over 2\mathrm{i}}$

$\cos x = {\left(e^{\mathrm{i}x} + e^{-\mathrm{i}x} \right) \over 2}$

Kombinatorik

Fakultät

$n! = 1 \cdot 2 \cdot \dots \cdot n = \prod_{i=1}^{n} i$

0! = 1

Die Fakultät von 0 ist als 1 definiert, da ein leeres Produkt vorliegt.

Fakultäten für nichtnatürliche Zahlen (negative/gebrochene/komplexe) Zahlen sind nicht definiert, als Ersatz kann die Gammafunktion dienen.

Binomialkoeffizient („n über k“)

${n \choose k} = \frac{n!}{(n-k)! \cdot k!}$

Binomischer Lehrsatz und Pascalsches Dreieck

(a + b)⁰ = 1

(a + b)¹ = a + b

(a + b)² = a² + 2ab + b²

(a + b)³ = a³ + 3a²b + 3ab² + b³

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

…

$k = 0 \dots n$

$(a+b)^n = {n \choose 0}a^{n} + {n \choose 1}a^{n-1}b + {n \choose 2}a^{n-2}b^2 + \dots + {n \choose n-1}ab^{n-1} + {n \choose n}b^n$

$= \sum_{k=0}^n {n \choose k}a^{n-k} b^k$

Schreibt man die Koeffizienten von (a + b)ⁿ zeilenweise, d. h. die von (a + b)ⁿ in Zeile n, erhält man das Pascalsche Dreieck. n über k ist daher die k-te Zahl in der n-ten Reihe dieses Zahlendreiecks.

Stirlingformel

$n! \approx \left(\frac{n}{e}\right)^n \cdot \sqrt{2 \pi n}$

Der Relative Fehler $\frac{\epsilon}{n!}$ ist bei großem n klein. Das gilt nicht notwendigerweise für den absoluten Fehler. Es gilt: $n! = \left(\frac{n}{e}\right)^n \cdot \sqrt{2 \pi n} \cdot \left[1 + \mathcal{O}(1/n)\right]$

Summenformeln

Hintergrundinformation in den Artikeln Summe und Reihe. Erklärungen zum Summenzeichen ebenfalls im Artikel Summe.

Rechenregeln

$\sum_{i=1}^{n}c = n \cdot c$ (Summation über n konstante Glieder ist soviel wie Multiplikation mit n)

$\sum_{i=m}^{n}c = (n-m+1) \cdot c$ (Summation über n-m+1 konstante Glieder)

$\sum_{i=m}^{n}c \cdot a_i = c \cdot \sum_{i=m}^{n}a_i$ (Konstanter Faktor kann vor das Summenzeichen gezogen werden)

$\sum_{i=m}^{n}(a_i + b_i) = \sum_{i=m}^{n}a_i + \sum_{i=m}^{n}b_i$ (Reihenfolge der Summanden kann beliebig geändert werden)

Arithmetische Reihe

$\sum_{i=1}^n i = \frac{n(n+1)}{2}$ (Summe der ersten n natürlichen Zahlen, Der kleine Gauß)

$\sum_{i=m}^n i = \frac{n(n+1)-(m-1)m}{2} = \frac{(n+m)(n-m+1)}{2}$ (Summe eines Bereiches von m bis n natürlichen oder ganzen Zahlen)

$\sum_{i=1}^n (2i-1) = n^2$ (Summe der ersten n ungeraden Zahlen)

Potenzsummen

konstanter Exponent

$\sum_{i=1}^n i^2 = \frac{n(n+1)(2n+1)}{6}$ (Summe der ersten n Quadratzahlen)

$\sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2$ (Summe der ersten n Kubikzahlen)

$\sum_{i=1}^n i^4 = \frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}$ (Summe der ersten n Potenzen mit Exponenten 4)

$\sum_{i=1}^n i^5 = \frac {1}{12} n^2 \left(n + 1\right)^2 \left(2n^2 + 2n -1\right)$ (Summe der ersten n Potenzen mit Exponenten 5)

Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhaberschen Formel berechnet werden.

konstante Basis (geometrische Reihe)

$\sum_{i=0}^n k^i = \frac{k^{n+1} -1}{k-1}$ (Summe der Potenzen von k mit bis zu n aufsteigendem Exponenten von Null an)

$\sum_{i=0}^{\infty} k^i = \frac{1}{1-k} \qquad \text{mit} \quad |k|<1$ (unendliche geometrische Reihe)

$\sum_{i=1}^n k^i = \frac{k^{n+1} -k}{k-1}$ (Summe der Potenzen von k mit bis zu n aufsteigendem Exponenten)

$\sum_{i=1}^n k^{-i} = \frac{1-k^{-n}}{k-1}$ (Summe der negativen Potenzen von k mit bis zu n absteigendem Exponenten)

Eine auch für Halbringe geeignete effiziente Rekursionsformel ist

$\sum_{i=1}^n k^i =\begin{cases} 0 & n = 0 \\ k & n = 1 \\ k + k\cdot\sum_{i=1}^{n-1}k^i & n \text{ ungerade} \\ (1+k^{n/2})\cdot\sum_{i=1}^{n/2}k^i & n \text{ gerade.} \end{cases}$

Harmonische Reihe

$\sum_{i=1}^n \frac 1i \approx \ln(n)+ \gamma,$ mit der Euler-Mascheroni-Konstante γ (gamma).

Summen mit Binomialkoeffizienten

$\sum_{k=0}^{n}{n \choose k} a^{n-k}b^{k} = (a+b)^n \qquad (a,b \in \mathbb{R} \text{ und } n \in \mathbb{N})$ (Binomischer Lehrsatz)

Spezialfälle dieser Formel sind:

• $\sum_{k=0}^{n} {n \choose k} = 2^n$ (setze a = 1,b = 1)
• $\sum_{k=0}^{n} (-1)^k{n \choose k} = 0$ (setze a = − 1,b = 1)
• $\sum_{k=0}^{n} {n \choose k} q^k = (q + 1)^n$ (setze a = q,b = 1)

Eine weitere Eigenschaft der Binomialkoeffizienten, die sich am pascalschen Dreieck ablesen lässt, ist die folgende:

$\sum_{i=0}^{n-1} {i \choose k} = {n \choose k+1}$