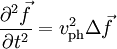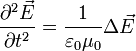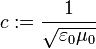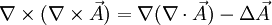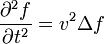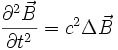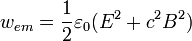EM-Welle

Als elektromagnetische Welle bezeichnet man eine Welle aus gekoppelten elektrischen und magnetischen Feldern. Zu ihnen gehören unter anderem Radiowellen, Mikrowellen, Infrarotstrahlung, sichtbares Licht, UV-Strahlung sowie Röntgen- und Gammastrahlung – kurz, das gesamte elektromagnetische Wellenspektrum. Der einzige Unterschied zwischen diesen Wellentypen liegt in ihrer Frequenz und somit ihrer spezifischen Energie. Es gibt jedoch ein kontinuierliches Spektrum (siehe Grafik unten); die Einteilung in die oben genannten Typen beruht auf den sich mit der Frequenz kontinuierlich ändernden Eigenschaften der Strahlung oder ihrer Herkunft sowie auf den davon abhängigen unterschiedlichen Verwendungen oder Herstellungsverfahren oder den verschiedenen dafür benutzten Messmethoden.

Anders als z. B. Schallwellen, benötigen elektromagnetische Wellen kein Medium, um sich auszubreiten.^[1] Sie pflanzen sich im Vakuum unabhängig von ihrer Frequenz mit Lichtgeschwindigkeit fort. Im freien Raum treten sie als Transversalwellen auf, d. h. die elektromagnetischen Feldvektoren sind senkrecht zur Ausbreitungsrichtung der Welle orientiert.

Elektromagnetische Wellen verhalten sich immer auch wie Teilchen (siehe Welle-Teilchen-Dualismus). Diese nennt man Photonen. Welches Verhalten bei einem Experiment mehr in den Vordergrund tritt, hängt davon ab, ob die Wellenlänge größer oder kleiner als die „charakteristische Ausdehnung“ (etwa eine Spaltbreite oder der Wirkungsquerschnitt oder die Ortsunschärfe beteiligter Teilchen) des Versuches ist.

Links: Die elektrische und magnetische Komponente einer elektromagnetischen Welle, die sich nach rechts ausbreitet (Fernfeld). λ ist die Wellenlänge
Rechts: Momentanaufnahme der beiden Komponenten, wenn die Welle auf den Beobachter zukommt.

Eigenschaften

Wellencharakter

Physikalisch betrachtet handelt es sich bei elektromagnetischen Wellen um sich ausbreitende Schwingungen des elektromagnetischen Feldes. Hierbei stehen elektrisches und magnetisches Feld bei linear polarisierten Wellen senkrecht aufeinander und haben ein festes Größenverhältnis. Dieses ist gerade durch die Wellenimpedanz gegeben. Insbesondere verschwinden elektrisches und magnetisches Feld an denselben Orten zur selben Zeit, so dass die häufig gelesene Darstellung, dass sich elektrische und magnetische Energie zyklisch ineinander umwandeln, im Fernfeld nicht richtig ist. Sie stimmt allerdings z. B. für das Nahfeld eines elektromagnetische Wellen erzeugenden elektrischen Dipols oder Schwingkreises.

Die Entstehung elektromagnetischer Wellen erklärt sich aus den maxwellschen Gleichungen: Die zeitliche Änderung des elektrischen Feldes ist stets mit einer räumlichen Änderung des magnetischen Feldes verknüpft. Ebenso ist wiederum die zeitliche Änderung des magnetischen Feldes mit einer räumlichen Änderung des elektrischen Feldes verknüpft. Für periodisch (insbesondere sinusförmig) wechselnde Felder ergeben diese Effekte zusammen eine fortschreitende Welle.

Beispiele für Experimente, in denen der Wellencharakter zum Tragen kommt:

• Erscheinungen wie Kohärenz und Interferenz lassen sich nur mit dem Wellenmodell erklären, weil die Mindestabmessungen der entsprechenden Versuche deutlich größer sind als die Wellenlänge des Lichts.
• Man könnte die von Rundfunksendern emittierte Strahlung als sehr große Anzahl von Photonen betrachten. Es gibt allerdings kein Messgerät, das derart energiearme Photonen einzeln nachweisen könnte. Es ist auch deshalb nicht zielführend, hier das Teilchenmodell zur Erklärung von Effekten heranzuziehen. Da die Antennen etwa die Größe der Wellenlänge haben, muss man für alle physikalischen Erklärungen die Welleneigenschaft der Strahlung betrachten.

Teilchencharakter

Für bestimmte Eigenschaften elektromagnetischer Wellen (z. B. Photoelektrischer Effekt), genügt das oben beschriebene Wellenmodell nicht mehr, um alle beobachtbaren Phänomene zu beschreiben, vielmehr treten die Teilcheneigenschaften einzelner Photonen, der Quanten des elektromagnetischen Feldes, in den Vordergrund. Der Wellencharakter (etwa Interferenz) bleibt aber voll erhalten. Man spricht deshalb vom Dualismus von Teilchen und Welle.

Im Rahmen dieser Teilchenvorstellung des Lichtes wird jeder Frequenz f die Energie eines einzelnen Photons 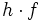$h\cdot f$ zugeordnet, wobei h das Plancksche Wirkungsquantum ist. Andererseits haben auch Teilchen, wie z. B. über mehrere Atome hinweg bewegte Elektronen, Welleneigenschaften (siehe auch Elektrischer Strom). Beide Aspekte elektromagnetischer Wellen werden theoretisch im Rahmen der Quantenelektrodynamik erörtert.

Beispiele für Wirkungen, in denen der Teilchencharakter zum Tragen kommt:

• Beim Compton-Effekt trifft eine elektromagnetische Welle mit etwa 20 pm Wellenlänge auf ein Elektron, dessen Wirkungsquerschnitt um etwa drei Größenordnungen kleiner ist. Zur Erklärung des physikalischen Ablaufes der Wechselwirkung muss also der Teilchencharakter des Lichts herangezogen werden. Jeder Versuch, die beobachtete Änderung der Wellenlänge mit dem Wellenmodell zu erklären, scheitert.
• Beim photoelektrischen Effekt ist das Verhältnis der Wellenlänge zum Wirkungsquerschnitt eines Elektrons noch größer. Also kann auch hier das Wellenmodell nichts zur Erklärung beitragen. Im Gegenteil - es führt zu offensichtlichen Widersprüchen.
• Die Erzeugung von Laserlicht beruht auf den Eigenschaften einzelner Atome, die jeweils erheblich kleiner sind als die erzeugte Wellenlänge. Deshalb muss man für die Erklärung der Herstellung auf das Photonenmodell zurückgreifen.

Photonen mit genügender Energie (etwa von einigen Elektronvolt aufwärts) wirken auf Materie ionisierend und können chemische (photochemische) Wirkungen auslösen, wenn die Bindungsenergien überschritten werden (Fotochemie). Diese chemische Wirksamkeit wird gelegentlich als Aktinität bezeichnet.

Wellen im Medium

In einem Medium (also in Materie) verringert sich die Geschwindigkeit abhängig von der Permittivität (dielektrische Leitfähigkeit $\varepsilon$) und der Permeabilität (magnetische Leitfähigkeit μ) des Stoffes. Es gilt dann: 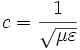$c=\frac{1}{\sqrt{\mu \varepsilon}}$. Zudem wird sie abhängig von der Frequenz ω der Welle (Dispersion), sowie (je nach Medium) abhängig von ihrer Polarisation und ihrer Ausbreitungsrichtung gebrochen. Eine direkte Krafteinwirkung (z. B. Richtungsänderung) auf eine sich ausbreitende elektromagnetische Welle kann nur durch das Ausbreitungsmedium (Begrenzungen wie Spiegel eingeschlossen) oder die Gravitationskraft erfolgen.

Einige neuere spekulative Theorien, zum Beispiel die Schleifenquantengravitation, sagen eine geringe Frequenzabhängigkeit der Lichtgeschwindigkeit c im Vakuum voraus.

Spektrum

Elektromagnetische Wellen sind im elektromagnetischen Spektrum nach der Wellenlänge sortiert (eine Liste von Frequenzen und Beispiele elektromagnetischer Wellen gibt es im dortigen Artikel).

Das am besten bekannte und am meisten studierte Beispiel einer elektromagnetischen Welle ist das sichtbare Licht. Es stellt nur einen winzigen Teil des gesamten Spektrums dar und ist der einzige Bereich, der von Menschen ohne technische Hilfsmittel wahrgenommen werden kann. Bei niedrigeren Frequenzen ist die Energie der Photonen zu gering, um chemische Prozesse auslösen zu können. Bei höheren Frequenzen hingegen beginnt der Bereich der ionisierenden Strahlung (Radioaktivität), bei der ein einziges Photon Moleküle zerstören kann.

Beim Licht bestimmt die Frequenz die Farbe des Lichtes und nicht, wie oft fälschlicherweise angenommen, die Wellenlänge. Deutlich wird dies, wenn man Licht in optisch dichteren Medien beobachtet, wo es sich mit einer geringeren Geschwindigkeit als c ausbreitet. Die Frequenz wird beim Übergang in optisch dichtere Medien nicht beeinflusst und folglich muss es laut 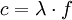$c = \lambda \cdot f \$ eine kürzere Wellenlänge haben. Da sich die Farbe aber im Medium nicht ändert, ist also nur die Frequenz charakteristisch für die Farbe des Lichts. In Spektren wird aus historischen Gründen jedoch immer noch die Wellenlänge als charakteristische Eigenschaft für Licht angegeben. Dieser Zusammenhang zwischen Farbe und Wellenlänge gilt dann aber nur im Vakuum (und in guter Näherung in Luft). Monochromatisches Licht, also Licht nur einer einzigen Wellenlänge, hat stets eine Spektralfarbe.

Datei:Electromagnetic spectrum c.svg

Biologische und chemische Wirkung

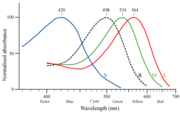Empfindlichkeitsverteilung der drei Zapfenarten beim Menschen. Schwarz gezeichnet ist die Empfindlichkeit der Stäbchen. Andere Primaten haben abweichende Empfindlichkeitsverteilungen.

Kleine Mengen Photonen mit einer Frequenz unterhalb von 4·10¹⁴ Hz (Wellenlänge über 0,7 µm und Energie unter 1,7 eV; im oberen Bild rechts vom sichtbaren Licht, also Mikrowellen und Rundfunkwellen) können keine chemischen Reaktionen an Molekülen bewirken, die bei Zimmertemperatur stabil sind. Damit kann man nur Wasserstoffbrückenbindungen beeinflussen, die deutlich schwächer als die Bindungskräfte innerhalb eines Moleküls sind und wegen der ständigen Bewegung der Atome nur Bruchteile einer Sekunde bestehen bleiben.

Das Molekül des Fotorezeptors Rhodopsin benötigt je nach Bauart mindestens ein Photon der Wellenlänge 700 nm oder kürzer, um mit einer Konformationsänderung zu reagieren, die dann vom Nervensystem weiter verarbeitet wird. Diese notwendige Wellenlänge kann durch Modifikationen der Molekülbauform geändert werden, wie im Bild rechts zu sehen ist. Die Mindestenergie der Photonen ist auch der Grund, wieso kein Lebewesen existiert, das Infrarot durch Nachweis von Einzelphotonen sehen kann. Entsprechend können Lebewesen ohne technische Hilfsmittel auch nicht auf Radiowellen geringer Intensität reagieren. Sehr starke Strahlung dieser großen Wellenlänge wirkt aber erwärmend, weil sie durch das Gewebe absorbiert wird.

Erreicht oder übersteigt die Energie von Photonen die Bindungsenergie eines Moleküls, kann jedes Photon ein Molekül zerstören und es können biologische Wirkungen wie beispielsweise eine beschleunigte Alterung der Haut oder Hautkrebs auftreten. Chemische Bindungsenergien stabiler Moleküle liegen oberhalb von etwa 3 eV pro Bindung, deshalb müssen Photonen mindestens diese Energie besitzen, soll es zu Moleküländerungen kommen.

Photonen von Röntgenstrahlung und Gammastrahlung besitzen so viel Energie, dass jedes davon viele Moleküle zerstören kann. Das bezeichnet man als Ionisierende Strahlung.

Abgrenzung

Sehr viele Photonen mit Frequenzen unterhalb von 10¹⁴ Hz, beispielsweise im Mikrowellenherd bewirken einen allgemeinen Energieeintrag und damit eine Erhöhung der Temperatur. Diese kann - wie jede anders verursachte Überhitzung auch - die Struktur biologischer Moleküle ändern. Das hat mit den Eigenschaften von Photonen nichts zu tun.

Das empfindliche Grubenorgan gewisser Schlangen reagiert nicht auf einzelne Photonen wie die Zellen der Netzhaut, sondern auf die Temperaturerhöhung, die durch die Gesamtenergie aller auftreffenden Photonen eingebracht wird.

Lichtgeschwindigkeit und spezielle Relativitätstheorie

Wie schnell sich Licht ungefähr ausbreitet, war seit 1676 bekannt. Allerdings fehlte bis 1865 jeder Zusammenhang zu anderen physikalischen Erscheinungen. Diesen konnte damals James Clerk Maxwell herstellen, der aus gewissen mathematischen Beziehungen seiner Maxwellgleichungen die Existenz elektromagnetischer Wellen vorhersagte. Deren Geschwindigkeit stimmte mit der damals bereits gut bekannten Lichtgeschwindigkeit so gut überein, dass sofort ein Zusammenhang hergestellt wurde. Diese Wellen konnte Heinrich Hertz 1888 experimentell nachweisen.

In der klassischen Mechanik werden Wellen durch die Wellengleichung

$\frac{\partial^2 \vec f}{\partial t^2} = v_{\text{ph}}^2 \Delta \vec f$

beschrieben. Hierbei bezeichnet 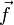$\vec f$ die Auslenkung der Welle und v_ph ihre Phasengeschwindigkeit, die hier als Ausbreitungsgeschwindigkeit der Welle interpretiert werden kann.

Aus den Maxwellgleichungen lässt sich nun im Vakuum für die elektrische Feldstärke 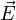$\vec E$ die Beziehung

$\frac{\partial^2 \vec E}{\partial t^2} = \frac{1}{\varepsilon_0\mu_0} \Delta \vec E$

herleiten (in SI-Einheiten; siehe Abschnitt Mathematische Beschreibung). Die Elektrische Feldstärke verhält sich in dieser Beziehung also wie eine Welle; die Größe

$c := \frac{1}{\sqrt{\varepsilon_0\mu_0}}$

tritt als Ausbreitungsgeschwindigkeit auf. Diese Geschwindigkeit c hat eine bemerkenswerte Form: Sie ist ausschließlich aus fundamentalen Naturkonstanten zusammengesetzt, die unabhängig vom Bezugssystem des Betrachters sind, was sich folglich auf die Größe c überträgt.

Situation am Teich: Der bewegte Beobachter sieht die Ausbreitungsgeschwindigkeit einer Wasserwelle um seine eigene Geschwindigkeit verringert. Maxwell sagt für elektromagnetische Wellen voraus, dass die Ausbreitungsgeschwindigkeit c für beide Beobachter gleich ist.

Grundlage der klassischen Mechanik ist das galileische Relativitätsprinzip, das besagt, dass die Naturgesetze in allen Inertialsystemen − solchen Bezugssystemen, in denen Körper, auf die keine Kraft wirkt, sich geradlinig fortbewegen − dieselbe Form haben (Galilei-Invarianz). Ein sich zu einem Inertialsystem mit konstanter Geschwindigkeit fortbewegendes Bezugssystem ist ebenfalls ein Inertialsystem.

Nach diesem Relativitätsprinzip wäre nun zu erwarten, dass ein Beobachter, der sich mit einer konstanten Geschwindigkeit relativ zur elektromagnetischen Welle bewegt, eine unterschiedliche Ausbreitungsgeschwindigkeit misst, wie etwa auch ein mit konstanter Geschwindigkeit fortbewegender Spaziergänger am Rande eines Teiches eine andere Ausbreitungsgeschwindigkeit einer Wasserwelle auf dem Teich feststellen würde als ein ruhender Beobachter. Die Maxwellgleichungen sagen aber für beide Beobachter die gleiche Ausbreitungsgeschwindigkeit voraus − sie sind nicht Galilei-invariant.

Dieser Widerspruch zur klassischen Mechanik löst sich allerdings nicht zu Ungunsten der Maxwellgleichungen auf: Die Tatsache, dass sich elektromagnetische Wellen (also Licht in einem weiter gefassten Sinne) in allen Inertialsystemen mit der gleichen Geschwindigkeit ausbreiten − die vielzitierte Konstanz der Lichtgeschwindigkeit − bildet ein Postulat Einsteins 1905 veröffentlichter spezieller Relativitätstheorie, die experimentell sehr gut bestätigt ist. An Stelle der Galilei-Invarianz tritt die sogenannte Lorentz-Invarianz.

Mathematische Beschreibung

Herleitung der elektromagnetischen Wellengleichung

Die zur Wellenausbreitung gehörigen mathematischen Beziehungen lassen sich auf Basis der maxwellschen Gleichungen nachvollziehen. Insbesondere lässt sich dieselbe Wellengleichung herleiten, mit der sich auch Schallwellen ausbreiten, obwohl dort völlig andere, rein mechanische Grundlagen maßgebend sind.

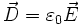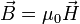Eine elektromagnetische Welle breite sich im Vakuum aus, und zwar im ladungsfreien Raum unter Ausschluss von dielektrischen, dia- und paramagnetischen Effekten ($\vec D = \varepsilon_0 \vec E$ und $\vec B = \mu_0 \vec H$, siehe Materialgleichungen der Elektrodynamik). Die Stromdichte 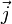$\vec{j}$ und Ladungsdichte 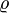$\varrho$ betragen null.

Ausgehend von der dritten maxwellschen Gleichung

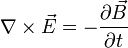
$\nabla\times\vec E = -\frac{\partial\vec B}{\partial t}$		(1)

wendet man auf beide Seiten den Rotationsoperator an. Dadurch erhält man:

$\nabla\times(\nabla\times\vec E) = -\nabla\times\left( \frac{\partial\vec B}{\partial t} \right) = -\mu_0 \frac{\partial}{\partial t} \left( \nabla\times\vec H \right)$.

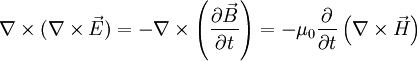Setzt man darin die vierte maxwellsche Gleichung (mit 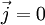$\vec{j}=0$) ein,

$\nabla\times H= \frac{\partial D}{\partial t}$,

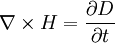ergibt sich

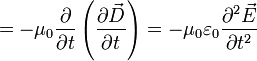
$= -\mu_0 \frac{\partial}{\partial t} \left( \frac{\partial\vec D}{\partial t} \right)= -\mu_0 \varepsilon_0 \frac{\partial^2\vec E}{\partial t^2}$		(2)

Dazu gilt ganz allgemein die vektoranalytische Beziehung

$\nabla\times(\nabla\times\vec A) = \nabla(\nabla\cdot\vec A) - \Delta\vec A$

mit dem Laplace-Operator

$\Delta = \frac {\partial^2}{\partial x^2} + \frac {\partial^2}{\partial y^2} + \frac {\partial^2}{\partial z^2}$.

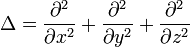Wendet man diese Beziehung auf 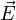$\vec E$ an und berücksichtigt, dass der ladungsfreie Raum betrachtet wird, in dem nach der ersten Maxwellschen Gleichung die Divergenz von 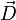$\vec D$ null beträgt, so folgt:

$\nabla\times(\nabla\times\vec E) = \nabla(\nabla\cdot\vec E) - \Delta\vec E = -\Delta \vec E$.		(3)

Setzt man nun (2) und (3) zusammen, ergibt sich folgende Wellengleichung:

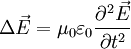$\Delta \vec E = \mu_0\varepsilon_0 \frac{\partial^2\vec E}{\partial t^2}$.		(4)

Fast alle Wellen lassen sich durch Gleichungen der Form

$\frac{\partial^2 f}{\partial t^2} = v^2 \Delta f$

beschreiben, wobei v die Ausbreitungsgeschwindigkeit der Welle ist. Für die Ausbreitungsgeschwindigkeit elektromagnetischer Wellen, die Lichtgeschwindigkeit c, gilt daher:

$c^2 = \frac{1}{\mu_0\varepsilon_0}$.

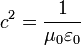Damit erhält man aus (4) die Gleichung

$\frac{\partial^2 \vec E}{\partial t^2} = c^2 \Delta \vec E$.

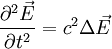Analog kann man für die magnetische Flussdichte 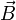$\vec B$ die Beziehung

$\frac{\partial^2 \vec B}{\partial t^2} = c^2 \Delta \vec B$

herleiten. Die Lösungen dieser Gleichungen beschreiben Wellen, die sich mit Lichtgeschwindigkeit c ausbreiten. Breitet sich die elektromagnetische Welle in isotropem Material mit der Dielektrizitätskonstante $\varepsilon$ und der Permeabilität μ aus, beträgt die Ausbreitungsgeschwindigkeit c:

$c = \frac{1}{\sqrt{\mu \varepsilon}}$.

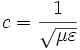Darin sind aber im Allgemeinen die Materialkonstanten nicht linear, sondern können selbst z. B. von der Feldstärke oder der Frequenz abhängen. Während Licht sich in der Luft immer noch fast mit Vakuumlichtgeschwindigkeit c ausbreitet (die Materialkonstanten sind in guter Näherung 1), gilt das für die Ausbreitung in Wasser nicht, was u. a. den Tscherenkow-Effekt ermöglicht.

Das Verhältnis der Vakuumlichtgeschwindigkeit zur Geschwindigkeit im Medium wird als Brechzahl n bezeichnet.

$n=\sqrt{\frac{\mu\varepsilon}{\mu_0\varepsilon_0}}=\sqrt{\mu_r\varepsilon_r}$,

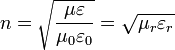wo μ_r und 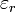$\varepsilon_r$ die relative Permeabilität und die relative Permittivität des Mediums bezeichnen.

Ausbreitung elektromagnetischer Wellen

Mit Hilfe der Maxwellgleichungen lassen sich aus der Wellengleichung noch weitere Schlüsse ziehen. Betrachten wir eine allgemeine Welle für das Elektrische Feld

$\vec{E}=\vec{E}_0 f(\hat{k}\cdot\vec{x}-ct)$,

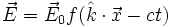wo 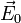$\vec{E}_0$ die (konstante) Amplitude ist, f eine beliebige -Funktion, 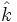$\hat{k}$ ein Einheitsvektor, der in Propagationsrichtung zeigt, und 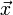$\vec{x}$ ein Ortsvektor. Zunächst sieht man durch Einsetzen in die Wellengleichung, dass 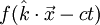$f(\hat{k}\cdot\vec{x}-ct)$ die Wellengleichung erfüllt, dass also

$\Delta f(\hat{k}\cdot\vec{x}-ct) = \frac{1}{c^2}\frac{\partial^2}{\partial t^2} f(\hat{k}\cdot\vec{x}-ct)$.

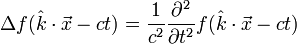Damit 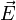$\vec{E}$ nun eine elektromagnetische Welle beschreibt, muss es aber nicht nur die Wellengleichung erfüllen, sondern auch die Maxwellgleichungen. Das bedeutet zunächst

$\nabla\cdot\vec{E}=\hat{k}\cdot\vec{E}_0 f'(\hat{k}\cdot\vec{x}-ct) = 0$,

$\vec{E}\cdot\hat{k} = 0$.

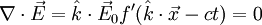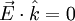Das elektrische Feld steht also stets senkrecht zur Propagationsrichtung, es handelt sich also um eine Transversalwelle.

Einsetzen von 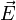$\vec{E}$ in eine weitere Maxwellgleichung ergibt

$\nabla\times\vec{E}=\hat{k}\times\vec{E}_0 f'(\hat{k}\cdot\vec{x}-ct) = -\frac{\partial B}{\partial t}$,

$\vec{B}=\frac{1}{c}\hat{k}\times\vec{E}$.

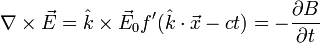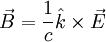Die magnetische Flussdichte in der elektromagnetischen Welle steht also ebenfalls senkrecht zur Propagationsrichtung und auch senkrecht zum elektrischen Feld. Weiters sind ihre Amplituden proportional zueinander:

$E_0=c\cdot B_0$.

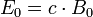In natürlichen Einheiten (c = 1) sind die Amplituden sogar gleich.

Mit dieser Beziehung lässt sich auch eine Aussage über die Energiedichte des elektromagnetischen Felds

$w_{em}=\frac{1}{2}\varepsilon_0(E^2+c^2 B^2)$

für den Fall der elektromagnetischen Welle herleiten:

$w_{em}=\varepsilon_0 E^2 = \frac{1}{\mu_0} B^2$.

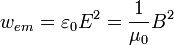Einzelnachweise

1. ↑ Gerthsen Physik. 22. Auflage, S. 177

Literatur

• Claus Müller: Grundprobleme der mathematischen Theorie elektromagnetischer Schwingungen. Springer, 1957. 
• K. Küpfmüller und G. Kohn: Theoretische Elektrotechnik und Elektronik, Eine Einführung. 16. Auflage. Springer, 2005, ISBN 3-540-20792-9. 
• Károly Simonyi: Theoretische Elektrotechnik. 10. Auflage. Barth Verlagsgesellschaft, 1993, ISBN 3-335-00375-6. 

Siehe auch

• Radar
• Funktechnik

Weblinks

• Versuche und Aufgaben
• Umrechnung: Frequenz in Wellenlänge und zurück – Elektromagnetische Wellen und Schallwellen
• Forscher machen erstmals Lichtwellen sichtbar
• Elektromagnetische Strahlung
• Einfache Simulation zur Ausbreitung von elektromagnetischer Strahlung

Elektromagnetisches Spektrum

Radiowellen | Mikrowellen | Terahertzstrahlung | Infrarotstrahlung | Sichtbares Spektrum | Ultraviolettstrahlung | Röntgenstrahlung | Gammastrahlung