- Perfekter Zipf
-
Dieser Artikel befasst sich mit dem Echten Zipfschen Gesetz. Für das sogenannte Falsche siehe Falsches Zipfsches Gesetz. 
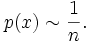
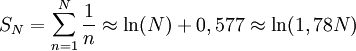
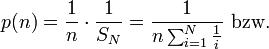
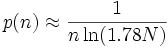
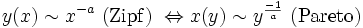
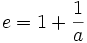
- e = 2
- einerseits aus dem Wunsch, eine Information möglichst verständlich zu vermitteln, was zu Wiederholung (Redundanz) und Ausführlichkeit führt, und
- andererseits aus Sparsamkeit, dem Bedürfnis, möglichst wenig physische und geistige Energie bei der Sprachproduktion aufzuwenden.
- Yule-Verteilung (nach George Udny Yule)
- Bradfordsches Gesetz
- Zeta- bzw. Zipf-Verteilung
- Helmut Birkhan: Das „Zipfsche Gesetz“, das schwache Präteritum und die germanische Lautverschiebung, Verl. d. Österr. Akad. d. Wiss., 1979 ISBN 3700102852
- David Crystal: Die Cambridge Enzyklopädie der Sprache. Campus, Frankfurt/ New York 1993, ISBN 3-593-34824-1
- X. Gabaix: Zipf's law for cities: An explanation. In: Quarterly Journal of Economics 114 (3): 739-767 AUG 1999
- Henry Guiter, M.V. Arapov (eds.): Studies on Zipfs Law. Brockmeyer, Bochum 1982, ISBN 3-88339-244-8
- M. Marsili, Y.C. Zhang: Interacting individuals leading to Zipf's law. In: Physical Review Letters 80 (12): 2741-2744 MAR 23 1998
- George Kingsley Zipf: The Psycho-Biology of Language. An Introduction to Dynamic Philology. The M.I.T. Press, Cambridge, Mass. 1935/ 1968
- George Kingsley Zipf: Human Behavior and the Principle of Least Effort. An Introduction to Human Ecology. Addison-Wesley Press, Cambridge, Mass. 1949
- http://www.nslij-genetics.org/wli/zipf/ - Umfangreiche Bibliografie
- http://arxiv.org/abs/cs.CL/0406015 - Zipf's law and the creation of musical context
- http://wortschatz.uni-leipzig.de/html/faq/hkl.html - Zipf'sches Gesetz am Beispiel Deutscher Wortschatz
- Zipf, Power-laws and Pareto
- Use of Hermetic Word Frequency Counter to Illustrate Zipf's Law
- B. McCOWAN et al.: The appropriate use of Zipf’s law in animal communication studies. ANIMAL BEHAVIOUR, 2005, 69, F1–F7
- Das Zipfsche Gesetz in den Primfaktoren der Fibonacci Zahlen
- Das Zipfsche Gesetz in der logistischen Gleichung
Das Zipf'sche Gesetz (nach George Kingsley Zipf, der dieses Gesetz in den 1930er Jahren aufstellte) ist ein Modell, mit dessen Hilfe man bei bestimmten Größen, die in eine Rangfolge gebracht werden, deren Wert aus ihrem Rang abschätzen kann. Häufige Verwendung findet das Gesetz in der Linguistik, speziell in der Korpuslinguistik und Quantitativen Linguistik, wo es zum Beispiel die Häufigkeit von Wörtern in einem Text zur Rangfolge in Beziehung setzt. Das Zipfsche Gesetz markierte den Beginn der Quantitativen Linguistik.
Ihm liegt ein Potenzgesetz zugrunde, das von der Pareto-Verteilung mathematisch beschrieben wird.
Daneben heißt auch eine Beobachtung zur Sparsamkeit beim Gebrauch einer Sprache (irrtümlicherweise) zipfsches Gesetz (siehe unten)
Inhaltsverzeichnis |
Einfache Zipfverteilung
Die vereinfachte Aussage des Zipfschen Gesetzes lautet: Wenn die Elemente einer Menge – beispielsweise die Worte eines Textes – nach ihrer Häufigkeit geordnet werden, ist die Wahrscheinlichkeit p ihres Auftretens umgekehrt proportional zur Reihenfolge n:
Der Normierungsfaktor Summe(1/n) von 1 bis N lässt sich nur für endliche Mengen angeben, da die harmonische Reihe nicht konvergiert. Bei endlichem N gilt:
und damit:
Wahrscheinlichkeitsverteilung
Das Zipfsche Gesetz hat seinen Ursprung in der Linguistik. Es besagt, dass bestimmte Wörter viel häufiger auftreten als andere und die Verteilung einer Hyperbel 1/n ähnelt. Der Ordnungsparameter Rang n lässt sich als kumulative Größe beschreiben: Der Rang n ist gleichbedeutend mit der Anzahl aller Elemente, die genauso groß oder größer sind als n. Für Rang 1 gibt es genau ein Element, nämlich das größte. Für Rang 2 sind es zwei, nämlich das erste und das zweite Element, für 3 drei usw.
Zipf nimmt einen einfachen reziproken Zusammenhang zum Rang an: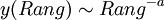 
. In der ursprünglichen Form ist das Zipfsche Gesetz frei von Parametern, es ist a = 1.
Die Zipfsche Verteilung entspricht genau der Pareto-Verteilung, unter Vertauschung von Ordinate und Abzisse:
Sie ist die Umkehrfunktion der Pareto-Verteilung. Wie diese ist sie eine kumulative Verteilungsfunktion, die einem Potenzgesetz gehorcht. Der Exponent e der Verteilungsdichtefunktion lautet entsprechend:
und für den einfachen Fall a = 1:
Beispiele
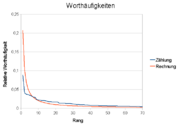
Die Verteilung der Worthäufigkeiten in einem Text, linke Grafik, gehorcht qualitativ einer einfachen Zipfschen Verteilung.
Das Zipfsche Gesetz gibt den Exponenten a der kumulativen Verteilungsfunktion vor: a=1.
Der Fitwert für die Worthäufigkeiten beträgt jedoch a=0.83, gleichbedeutend mit dem Exponenten apareto=1,20 einer Paretoverteilung und dem Exponenten e einer Potenz-Verteilungsdichtefunktion von e=2,20.
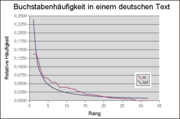
Auch die Verteilung der Buchstabenhäufigkeiten ähnelt einer Zipfschen Verteilung. Die Statistik mit 20–30 Buchstaben ist aber zu schlecht, um den Verlauf mit einer Potenzfunktion anzupassen.
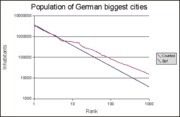
Ein weiteres Beispiel aus dem Artikel Pareto-Verteilung behandelt die Größenverteilung von Städten. Auch hier findet man eine Abhängigkeit, die einem Potenzgesetz gehorcht. Die Grafik rechts stellt die Zipf-Näherung den Messwerten gegenüber. Der lineare Verlauf in der doppeltlogarithmischen Verteilung stützt die Annahme eines Potenzgesetzes. Anders als die Vermutung von Zipf hat der Exponent nicht den Wert 1, sondern den Wert 0,77, entsprechend einem Exponenten einer Potenzdichteverteilung von e=2,3.
Die Bedeutung der Zipf-Verteilung liegt in der schnellen qualitativen Beschreibung von Verteilungen aus den unterschiedlichsten Bereichen, während die Pareto-Verteilung den Exponenten der Verteilung verfeinert.
Beispielsweise ist die Datenbasis für einen Fit bei der Angabe der Einwohnerzahl von nur 7 Städten zu klein. Das Zipfsche Gesetz liefert eine gute Näherung:
Rang n Stadt Einw. 1/Rang p(n) p(N)*Menschen Abweichung 1 Berlin 3522896 1 0,39 3531136,31 -0,23 2 Hamburg 1626220 0,5 0,19 1765568,15 -8,57 3 München 1206683 0,33 0,13 1177045,44 2,46 4 Köln 946280 0,25 0,1 882784,08 6,71 5 Frankfurt 635150 0,2 0,08 706227,26 -11,19 6 Dortmund 594058 0,17 0,06 588522,72 0,93 7 Essen 624445 0,14 0,06 504448,04 19,22
Die Schlagworte Potenzgesetz (power law), Skalengesetz oder Selbstorganisation suchen nach Antworten für das Auftreten von Potenzverteilungen.
Das „falsche“ Zipfsche Gesetz zur Sprechökonomie
Das Falsche Zipfsche Gesetz ist eine bedeutende als Gesetz formulierte Beobachtung zur Sparsamkeit im Gebrauch von Sprache, das Zipf vermutlich zu Unrecht zugeschrieben wird.
Dieses „falsche“ Zipfsche Gesetz besagt, dass Äußerungen in einer Sprache immer aus einem Kompromiss zwischen zwei entgegengesetzten Tendenzen im Sprecher entstehen:
Siehe auch
Literatur
Weblinks
Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot
Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta
Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis
Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda
Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt
Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial
Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma
Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.
