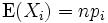Polynomialverteilung

Die Multinomialverteilung oder Polynomialverteilung ist eine diskrete Wahrscheinlichkeitsverteilung. Man kann sie als multivariate Verallgemeinerung der Binomialverteilung auffassen.

Modell und Definition

Ausgehend von einem sogenannten Urnenmodell mit Zurücklegen sind in der Urne q Sorten Kugeln. Der Anteil der Sorten Kugeln in der Urne ist $p_i (i = 1, \dots q)$. Der Urne wird n-mal jeweils eine Kugel entnommen, ihre Eigenschaft überprüft und danach wieder in die Urne zurückgelegt.

Man interessiert sich nun für die Anzahl X_i der Kugeln einer jeden Sorte i in dieser Stichprobe. Die Zahlen X_i genügen der Multinomialverteilung, denn sie besitzen die Wahrscheinlichkeiten:

$P(X_1=x_1 \and X_2=x_2 \and ... \and X_q=x_q)= \frac {n!}{x_1! \cdot x_2! \cdot ... \cdot x_q!}p_1^{x_1} \cdot p_2^{x_2} \cdot ... \cdot p_q^{x_q},$

wobei der Bruch Polynomialkoeffizient genannt wird.

Als Veranschaulichung kann man einen Würfel heranziehen. Man wirft diesen n-mal, hat dabei q=6 mögliche Ausgänge und interessiert sich dafür, wie groß die Wahrscheinlichkeit dafür ist, dass X₁=x₁-mal auftritt, X₂=x₂-mal und so weiter. Weiter beschreiben die jeweiligen p die Wahrscheinlichkeiten der Würfelflächen und somit ob es sich um einen fairen oder unfairen Würfel handelt.

Eigenschaften

Für jedes i ist die Zufallsvariable X_i binomialverteilt mit den Parametern n und p_i, hat also den Erwartungswert

$\operatorname{E}(X_i) = np_i$

und die Varianz

$\operatorname{Var}(X_i) = n p_i (1-p_i)$.

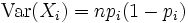Die Kovarianz zweier Zufallsvariablen X_i und X_j mit 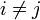$i\ne j$ berechnet sich als

${\rm Cov}(X_i,X_j) = -n\,p_i\,p_j$.

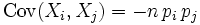Die Multinomialverteilung hat in Bayesscher Statistik als a-priori-Verteilung die Dirichlet-Verteilung.

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart