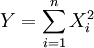Wishartverteilung

Die Wishart-Verteilung ist eine Wahrscheinlichkeitsverteilung. Sie ist die multivariate Entsprechung der χ²-Verteilung.

Für die Erläuterung wird zum besseren Verständnis zunächst von einer Zufallsvariablen ausgegangen: Man betrachtet eine standardnormalverteilte Zufallsvariable X, also mit dem Erwartungswert 0 und der Varianz 1. Es liegen von dieser Variablen n Beobachtungen oder Realisationen x_i (i=1, ... , n) vor. Da die Realisationen unabhängig voneinander stattfinden, interpretiert man sie als eine Folge von n standnormalverteilten Zufallsvariablen X_i. Die Quadratsumme dieser Zufallsvariablen

$Y = \sum_{i=1}^n X_i^2$

ist dann χ²-verteilt mit n Freiheitsgraden. Fasst man die Beobachtungen x_i in einem Vektor x mit n Elementen zusammen, kann man auch y darstellen als die Norm

$y = \underline x^T \underline x$,

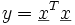wobei x^T ein Zeilenvektor ist.

Es werden nun p viele verschiedene Zufallsvariablen X_j betrachtet. Diese Zufallsvariablen sind gemeinsam normalverteilt mit dem Erwartungswert 0 und der Kovarianz-Matrix Σ. Es liegen für jede Zufallsvariable jeweils n viele Beobachtungen vor. Man kann nun diese Daten in einer (nxp)-Matrix X zusammenfassen:

$\underline X= \begin{pmatrix} x_{11}& x_{12}& \cdots &x_{1j}&\cdots &x_{1p}\\ x_{21}& x_{22}& \cdots &x_{2j}&\cdots &x_{2p}\\ \vdots& & & & &\vdots \\ x_{i1}& x_{i2}& \cdots &x_{ij}&\cdots &x_{ip}\\ \vdots& & & & &\vdots \\ x_{n1}& x_{n2}& \cdots &x_{nj}&\cdots &x_{np} \end{pmatrix}$.

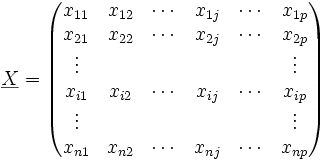Analog zu oben bildet man die symmetrische Matrix 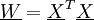$\underline W = \underline X^T\underline X$ mit den Elementen

$\underline W= \begin{pmatrix} \underline x_{1}^T \underline x_{1} & \underline x_{1}^T \underline x_{2}& \cdots & \underline x_{1}^T \underline x_{j}&\cdots & \underline x_{1}^T \underline x_{p}\\ \underline x_{2}^T \underline x_{1}& \underline x_{2}^T \underline x_{2}& \cdots & \underline x_{2}^T \underline x_{j}&\cdots & \underline x_{2}^T \underline x_{p}\\ \vdots& & & & &\vdots \\ \underline x_{j}^T \underline x_{1}& \underline x_{j}^T \underline x_{2}& \cdots & \underline x_{j}^T \underline x_{j}&\cdots & \underline x_{j}^T \underline x_{p}\\ \vdots& & & & &\vdots \\ \underline x_{p}^T \underline x_{1}& \underline x_{p}^T \underline x_{2}& \cdots & \underline x_{p}^T \underline x_{j}&\cdots & \underline x_{p}^T \underline x_{p} \end{pmatrix}$.

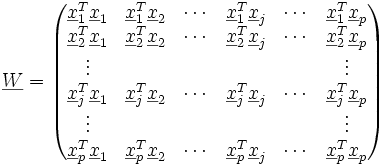Diese Matrix W ist nun Wishart-verteilt mit n Freiheitsgraden.

Eigenschaften der Wishart-Verteilung

Wie die χ²-Verteilung ist auch die Wishart-Verteilung reproduktiv: Die Summe von p Wishart-verteilten Zufallsvariablen mit n Freiheitsgraden und p Zufallsvariablen mit m Freiheitsgraden ist wieder insgesamt Wishart-verteilt mit m+n Freiheitsgraden.

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart