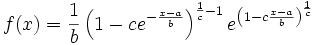- Jenkinson–von Mises Darstellung
-
siehe auch Grund auf Wikipedia:Qualitätssicherung/5. September 2006
Die Allgemeine Extremwertverteilung ist eine stetige Wahrscheinlichkeitsverteilung. Sie spielt eine herausragende Rolle in der Extremwerttheorie, da sie die wesentlichen möglichen Verteilungen von Extremwerten einer Stichprobe in einer Darstellung zusammenfaßt.
Inhaltsverzeichnis
Definition
Eine stetige Zufallsgröße X genügt einer Fischer-Tippett-Verteilung mit den Parametern a > 0 und b > 0, wenn sie die Wahrscheinlichkeitsdichte
besitzt.
Beziehung zu anderen Verteilungen
Beziehung zur Fischer-Tippett-Verteilung
Die Extremwertverteilung geht mit dem Parameter c = 1 zur Fischer-Tippett-Verteilung über.
Beziehung zur Gumbel-Verteilung
Die Extremwertverteilung geht mit den Parametern a = 0,b = 1 und c = 1 zur Gumbel-Verteilung über, die ein Spezialfall der Fischer-Tippett-Verteilung ist.
Siehe auch
- Rossi-Verteilung
- Frechet-Verteilung
- Extremwerttheorie
Diskrete univariate VerteilungenDiskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-MandelbrotDiskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | ZetaKontinuierliche univariate VerteilungenKontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-HalbkreisKontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambdaKontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | VoigtMultivariate VerteilungenDiskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet MultinomialKontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-GammaMultivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart
Wikimedia Foundation.