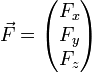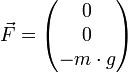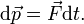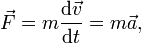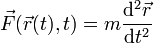Kräfteaddition

Physikalische Größe
Name	Kraft
Formelzeichen der Größe	F
Größen- und Einheiten- system Einheit Dimension SI 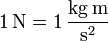$\mathrm{1\, N = 1\, \frac{kg\, m}{s^2}}$ m·L·t−2
Siehe auch: Schub; mechanischer Widerstand

Die Kraft ist eine physikalische Größe und ein grundlegender Begriff insbesondere der Mechanik, die die Beschleunigung von Massen oder die Verformung von Körpern verursacht. Sie ist eine Vektorgröße und tritt häufig als Feldgröße auf; man spricht in diesem Zusammenhang von einem Kraftfeld.

Das Formelzeichen der Kraft ist F (von frz./engl. force) und ihre Einheit ist das Newton (N), zu Ehren von Sir Isaac Newton, der mit seinen Bewegungsgesetzen den modernen physikalischen Kraftbegriff einführte.

Wort- und Begriffsgeschichte

Das Wort Kraft ist altgermanischen Ursprungs; im Englischen hat craft infolge der Konkurrenz durch Altfrz. force eine eingeengte Bedeutungsentwicklung genommen. In der physikalischen Fachsprache ist Kraft spätestens im 17. Jahrhundert mit Lat. vis, Frz. force gleichgesetzt worden (Isaac Newton: Mathematische Grundlagen der Naturphilosophie, 1687). Jenseits der Physik hat force im Engl. und Frz. breitere Bedeutungen als im Dt. und kann auch als Macht oder Stärke übersetzt werden (la force militaire d'un pays; la force du vent). Das griechische Wort für Kraft, δύναμις, lag der CGS-Einheit dyn zugrunde und lebt fort in Dynamik, was als physikalischer Fachbegriff der analytischen Mechanik die Lehre von der Bewegung unter dem Einfluss von Kräften bezeichnet.

Abgeleitet von „Kraft“ ist die Präposition kraft. Sie führt den Genitiv mit sich – was ihren Gebrauch zurückgehen lässt. Rechtssprachlich steht sie etwa in der Präambel zum Grundgesetz … hat das deutsche Volk kraft seiner verfassungsgebenden Gewalt … oder im Ausdruck kraft seines Amtes.

Im Deutschen bezeichnet Kraft eine körperliche oder geistige Voraussetzung zu bestimmten Handlungen (Muskelkraft; Krafttraining). In der zweiten Bedeutung – der Ausführung der Tätigkeit selbst (eine Kraft ausüben; unter der Kraft zusammenbrechen) kommt die Alltagsvorstellung von Kraft dem physikalischen Fachbegriff nahe. Der umgangssprachliche Kraftbegriff umfasst jedoch auch die Arbeitskraft oder die Schreibkraft, ferner Streitkräfte und allgemein Gruppen politischer Akteure (die fortschrittlichen/ konservativen/ … Kräfte). Der Begriff wurde früh auch sprachlich verallgemeinert, so in Heilkraft (getrockneter Kräuter oder eines bestimmten Wassers).

In der Rechtssprache bedeutet Kraft seit dem Mhd. Gültigkeit, heute nur noch in bestimmten Formeln: in/außer Kraft bleiben/treten/setzen, vgl. rechtskräftig. Aus in/durch Kraft entstand die Präposition kraft (kraft Amtes).

Als physikalischer Fachbegriff wurde Kraft von Archimedes eingeführt und von Galilei aufgegriffen. Isaac Newton präzisierte den Begriff Kraft in seinen 1687 veröffentlichten Bewegungsgesetzen. Bis weit ins 19te Jahrhundert benutzten Physiker das Wort Kraft jedoch auch in Bedeutungen, die nicht durch die newtonschen Gesetze gedeckt waren, und zwar insbesondere auch in der Bedeutung von Energie, denn der moderne Energiebegriff wurde (auf der Grundlage Leibniz’scher Prinzipien, „lebendige Kraft“, vis viva) erst mit dem ersten Hauptsatz der Thermodynamik (Julius Robert von Mayer, 1842) geschaffen.

Während die Kraft wie auch die Energie in der klassischen Physik über ihre Ursachen und Wirkungen differenziert betrachtet wird (Reibungskraft, Fliehkraft, Schwerkraft, kinetische Energie, potentielle Energie, Wärmeenergie usw.), unterscheidet die moderne Physik noch vier Grundkräfte und nennt sie auch Wechselwirkungen:

• Elektromagnetische Wechselwirkung
• Schwache Wechselwirkung
• Starke Wechselwirkung
• Gravitation

Die Erscheinungen, die durch den Magnetismus und „magnetische Kräfte“ beschrieben werden, sind lediglich ein relativistischer Nebeneffekt elektrischer Ströme.

Alle Kräfte lassen sich auf diese vier zurückführen. Eine wahrscheinliche Hypothese geht davon aus, dass auch sie in Wirklichkeit nur verschiedene Ausprägungen derselben Sache sind. Allerdings ist es bisher erst gelungen, die Elektromagnetische und die Schwache Wechselwirkung einheitlich zu erklären („Elektroschwache Wechselwirkung“).

Wirkung der Kraft

Kräfte erkennt man nur an ihren Wirkungen:

• Eine Kraft kann die Geschwindigkeit oder Bewegungsrichtung eines Körpers ändern.
• Ein Kräftepaar kann einen Körper verformen (Deformation).
  Davon gibt es zwei Arten:

1. Elastizität: Fähigkeit von Stoffen, eine Formänderung rückgängig zu machen, sobald die einwirkende Kraft wegfällt.
2. Plastizität (Duktilität): Vermögen eines Werkstoffes, seine Gestalt beizubehalten, die durch eine Krafteinwirkung entstanden ist.

Um eine Kraft zu beschreiben, genügt es nicht, Zahlenwert und Einheit anzugeben; notwendig ist zusätzlich die Angabe der Richtung, in der die die Kraft wirkt:

• Wenn die Kraft in die gleiche Richtung zeigt wie die Bewegungsrichtung des Körpers, auf den sie wirkt, beschleunigt sie ihn (Beschleunigung). Wenn die Kraft der Bewegungsrichtung entgegengesetzt ist, bremst sie ihn ab. Bei jedem anderen Winkel zwischen Kraft und Geschwindigkeit bewirkt die Kraft auch eine Richtungsänderung (Querbeschleunigung).
• Die Verformung eines Körpers kommt genau genommen nicht durch eine einzelne Kraft zustande, sondern dadurch, dass an verschiedenen Angriffspunkten verschiedene Kräfte wirken (Spannung). Je nachdem, wie diese Kräfte gerichtet sind, wird der Körper gedehnt, komprimiert oder verzerrt.

Eine physikalische Größe, die wie die Kraft erst durch die Angabe von Zahlenwert, Einheit und Richtung festgelegt ist, nennt man eine vektorielle Größe. Solche Größen kann man als Pfeile darstellen. In einem kartesischen Koordinatensystem hat ein Kraftvektor drei Komponenten:

$\vec F = \begin{pmatrix}F_x \\ F_y \\ F_z\end{pmatrix}$

Um beispielsweise die Gewichtskraft 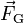$\vec F_\mathrm G$ zu beschreiben, mit der ein Körper der Masse m von der Erde angezogen wird, wählt man ein Koordinatensystem mit vertikaler z-Achse und erhält (mit der Erdbeschleunigung g)

$\vec F = \begin{pmatrix}\ 0\ \\ \ 0\ \\ -m \cdot g\end{pmatrix}$

Der Körper wird nach unten beschleunigt, deshalb ist die z-Komponente negativ, $-m \cdot g.$

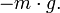
Um mechanische Spannungen zu beschreiben, muss man Kraft als ein vektorielles Feld auffassen: in jedem Angriffspunkt, bezeichnet durch den Ortsvektor 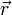$\vec r$, kann prinzipiell eine andere Kraft 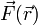$\vec F(\vec r)$ herrschen.

Kraft in den newtonschen Gesetzen

Zur Kraft gehört, dass sich entgegen gerichtete Kräfte nach den Regeln der Vektoraddition aufheben können. Ist das der Fall, herrscht ein Kräftegleichgewicht. Ein Körper bewegt sich geradlinig, solange die auf ihn wirkenden Kräfte im Gleichgewicht sind. Insbesondere bleibt ein ruhender Körper in Ruhe. Auf diesem ersten newtonschen Axiom beruht die gesamte Statik.

Nach dem zweiten newtonschen Axiom bewirkt eine Kraft 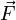$\vec{F}$, die auf einen freien Körper ausgeübt wird, eine Änderung von dessen Impuls 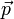$\vec{p}$: in jedem infinitesimal kurzen Zeitraum dt ändert sich der Impuls des Körpers um 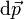$\mathrm{d}\vec{p}$ gemäß

$\mathrm{d}\vec{p}=\vec{F}\mathrm{d}t.$

Der Impuls eines Körpers hängt über 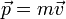$\vec{p}=m\vec{v}$ mit der Masse m und der Geschwindigkeit 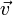$\vec{v}$ zusammen; da die Masse des Körpers bei geringen (nicht-relativistischen) Geschwindigkeiten nahezu konstant bleibt, schreibt man das zweite newtonsche Axiom meistens in der Form

$\vec{F} = m {\mathrm{d}\vec{v}\over\mathrm{d}t} = m \vec{a},$

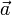wobei $\vec{a}$ für die auf den Körper wirkende Beschleunigung steht. Diese Gleichung ist der Prototyp einer Bewegungsgleichung: wenn die Kraft 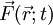$\vec{F}(\vec{r};t)$, sowie die Anfangsposition und Anfangsgeschwindigkeit eines Körpers gegeben sind, dann legt die Gleichung 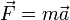$\vec{F}=m\vec{a}$ den gesamten weiteren Bewegungsverlauf des Körpers fest.

Die Hauptaufgabe der theoretischen Mechanik besteht darin, mit Hilfe der Vektoranalysis oder unter Nutzung des Lagrange- oder hamiltonsche Mechanik diese Berechnung tatsächlich auszuführen.

Die grundsätzliche, wenn auch nicht praktische Möglichkeit, aus gegebenen Anfangsbedingungen und Kräften die Bewegung beliebig komplizierter Systeme vorauszuberechnen, trug im 18. Jahrhundert zur Verbreitung eines mechanistischen Weltbildes bei.

Das mechanistische Weltbild erklärt gut konservative Systeme, aus denen keine Energie entweicht. In der Praxis kommen jedoch nicht nur konservative Kräfte vor, sondern auch Reibungskräfte, die zur Erzeugung von Wärme führen, was nichts anderes ist, als ungeordnete Bewegung auf mikroskopischem Niveau. Die Entropie jedes Systems erhöht sich somit unumkehrbar, man spricht auch vom Wärmetod. Die Thermodynamik ergänzt die Mechanik entsprechend.

Die Paradoxa der statistischen Mechanik, die Quantenmechanik und die Chaostheorie zeigten seit ungefähr 1900 grundsätzliche Grenzen der Berechenbarkeit in Modellen der klassischen Physik auf.

Messung von Kräften

Hauptartikel Kraftmessung

Die Definition der SI-Einheit Newton als abgeleitete Einheit, 1 N = 1 kg · m / s², beruht auf der Möglichkeit, gemäß 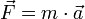$\vec F = m \cdot \vec a$ eine Kraft über die von ihr verursachte Beschleunigung zu messen.

Im Schulunterricht und in einigen anspruchslosen Anwendungen der Mechanik misst man Kräfte hingegen über die Verformung von Federn (die letztlich gegen 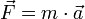$\vec F = m \cdot \vec a$ kalibriert sind). Dabei nutzt man das hookesche Gesetz, demzufolge eine nicht zu starke Ausdehnung (Überdehnung) einer Spiralfeder der ausgeübten Kraft proportional ist. Die Kraft für das Zusammendrücken oder Auseinanderziehen ist jeweils: 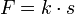$F=k\cdot s$, wobei s die Verlängerung oder Verkürzung bezeichnet. Der Ausdruck k steht für die Federeigenschaft (weich oder hart), der sogenannten Federkonstante mit der Einheit [N/m]. Je nach Wert dieser Konstanten, kann man große oder kleine Kräfte messen. Ist der Federweg z. B. 10 cm bei einer Feder mit k = 5 N/cm, dann ist das Produkt F = 5 N/cm · 10 cm = 50 N

Verschiedene Kräfte

Gewichtskraft, träge und schwere Masse

Die Gravitation macht sich als Schwerkraft oder, gleichbedeutend, Gewicht oder Gewichtskraft bemerkbar. Gewichtskraft ist die Kraft, mit der ein Körper von der Erde angezogen wird. Diese Kraft ist proportional zur Masse m des Körpers,

$\vec F_\mathrm G = m \cdot \vec g$.

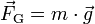Der Proportionalitätsfaktor g ist schwach ortsabhängig; im Schulunterricht wird er daher Ortsfaktor genannt. Er hat in Mitteleuropa den ungefähren Zahlenwert 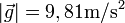$|\vec g|=9,81 \mathrm{m/s^2}$; für viele Anwendungen genügt es, mit der Näherung 10 m/s² zu rechnen.

Wenn man F_G in die linke Seite der newtonschen Bewegungsgleichung 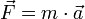$\vec F = m \cdot \vec a$ einsetzt, erhält man 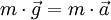$m \cdot \vec g = m \cdot \vec a$, wobei 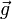$\vec g$ für einen senkrecht nach unten gerichteten Vektor mit Betrag g steht. Aus dieser Beziehung kürzt sich die Masse m heraus, so dass man den Ortsfaktor g als eine Beschleunigung, die Erdbeschleunigung, identifizieren kann; folglich hat g die Einheit m/s².

Dass die Masse eines Körpers sowohl in die Bewegungsgleichung 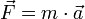$\vec F = m \cdot \vec a$ als auch in die Gewichtskraft 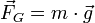$\vec F_G = m \cdot \vec g$ eingeht, ist vielleicht der erstaunlichste Befund der newtonschen Mechanik. Man hat zwischen träger Masse (in der Bewegungsgleichung) und schwerer Masse (in der Bestimmung der Gewichtskraft) unterschieden und experimentell Abweichungen gesucht, aber nicht gefunden.

Elektromagnetische Kräfte

Elektromagnetische Kräfte können als Anziehung oder Abstoßung zwischen elektrisch geladenen Körpern oder zwischen Magneten beobachtet werden. Viel bedeutsamer ist aber, dass solche Kräfte auch im Inneren von Materie wirken. Unsere Stoffwelt ist aus elektrisch positiv geladenen Atomkernen und negativ geladenen Elektronen zusammengesetzt. Positive und negative Ladungen kompensieren sich gegenseitig, so dass Alltagsgegenstände als ganze in der Regel elektrisch ungeladen sind. Selbst in elektrostatisch aufgeladenen Gegenständen herrscht, relativ gesehen, nur ein ganz geringer Elektronenüber- oder unterschuss. Deshalb sind die im Inneren von Materie wirkenden Kräfte um viele Größenordnungen stärker als elektrostatische Kräfte zwischen Alltagsgegenständen.

Im wesentlichen bestehen die elektromagnetischen Kräfte im Inneren von Materie aus der elektrostatischen Anziehung und Abstoßung zwischen Elektronen und Atomkerne sowie aus der Lorentzkraft, die auf in Magnetfeldern bewegte Elektronen wirkt.

Diese fundamentalen Kräfte machen sich in vielfältiger Weise bemerkbar:

• als Widerstand, den ein Körper einer Verformung entgegensetzt (Federkraft, Kompressibilität, Schubmodul);
• als Reibung zwischen den Oberflächen verschiedener Körper;
• als elektromotorische Kraft, die Elektronen durch einen Leiter treibt;
• in Fluiden als Kompressibilität und Viskosität.

Scheinkräfte

Wirkungen bei der Rotation

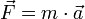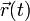Im einfachsten Anwendungsfall beschreibt die newtonsche Bewegungsgleichung $\vec F = m \cdot \vec a$ die Bewegung eines einzelnen Körpers in einem gegeben Kraftfeld. In dieser Gleichung steht $\vec a$ für die zweite Zeitableitung des Ortsvektors $\vec r(t)$ des Körpers; die Kraft 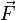$\vec F$ kann sowohl orts- als auch zeitabhängig sein. 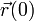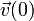Das volle mathematische Problem der newtonschen Mechanik lautet also, unter gegebenen Anfangsbedingungen $\vec r(0)$ und $\vec v(0)$ aus der vektoriellen Differentialgleichung

$\vec F (\vec r ( t), t) = m \frac{\mathrm d ^2 \vec r}{\mathrm d t^2}$

den zeitlichen Verlauf von 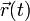$\vec r(t)$ zu bestimmen.

Die mathematische Struktur dieser Gleichung ist so anspruchsvoll, dass selbst eine so einfach formulierte Aufgabe wie die Berechnung einer Planetenbahn im Feld einer mit 1 / r² abnehmenden Zentralkraft im gymnasialen Schulunterricht in aller Regel unzugänglich bleibt. Nichtsdestoweniger sind Ergebnisse der newtonschen Mechanik längst in unser Alltagsdenken eingedrungen. Das wurde möglich, indem man an diese Ergebnisse eine eigene Begrifflichkeit geknüpft hat. Diese Begrifflichkeit besteht insbesondere aus einer ganzen Reihe von Scheinkräften, hinter denen sich partielle Lösungen oder Umformungen der newtonschen Gleichung verbergen. Beispiele für solche Scheinkräfte sind

• die Zentrifugalkraft, (Fliehkraft; siehe auch Zentripetalkraft);
• die Corioliskraft;

Ein Beispiel für einen anderen Begriff, der eine ganze Klasse von Kraftwirkungen zusammenfasst, ist das Drehmoment.

Eingeprägte Kräfte und Zwangskräfte, Auflagerkräfte

Um in der Technischen Mechanik technische Systeme (z. B. Tragwerke) einer Berechnung zugänglich zu machen, werden Bindungen zwischen den Körpern des Systems und zwischen dem System und seiner Umwelt, die nur geringe Formänderungen zulassen, als starre Bindungen idealisiert. Solche starren Bindungen sind in der Regel Gelenke zwischen den Körpern oder Lager. Damit geht der physikalische Charakter dieser Bindungen verloren, und die durch diese Bindungen bedingte mechanische Wechselwirkung der Körper wird durch die Zwangskräfte repräsentiert. Zwangskräfte verrichten am System keine Arbeit, da keine resultierende Bewegung stattfindet.

Im Gegensatz dazu stehen die eingeprägten Kräfte, die – wie oben erläutert – ihre Ursache in physikalischen Gesetzen haben. Eingeprägte Kräfte und Zwangskräfte erfüllen zusammen die Gleichgewichtsbedingungen.

Beispiele für Zwangskräfte: Normalkraft, Lagerkraft, Haftkräfte.

Beispiele für eingeprägte Kräfte: Gewichtskraft, Gleitreibungskraft, Seilkraft, Federkraft, Dämpferkraft, Kraft mit vorgegebenem Verlauf.

Zusammensetzung von Kräften

1. Kräfte mit derselben Richtung

Wirken zwei Kräfte, die auf den gleichen Punkt wirken, mit den Beträgen F₁ und F₂ in die gleiche Richtung, so muss man die beiden Kraftbeträge addieren, um den Betrag F der Gesamtkraft zu erhalten.

F = F₁ + F₂

2. Kräfte mit entgegengesetzter Richtung

Wirken zwei Kräfte, die auf den gleichen Punkt wirken, mit den Beträgen F₁ und F₂ in entgegengesetzter Richtung, so erhält man den Betrag F der Gesamtkraft dadurch, dass man vom größeren Kraftbetrag den kleineren subtrahiert. Die Richtung der Gesamtkraft stimmt mit der Richtung derjenigen Einzelkraft überein, die den größeren Betrag hat.

F = | F₁ − F₂ |

3. Kräfte mit unterschiedlicher Richtung

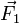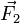Wirken zwei Kräfte in unterschiedlicher Richtung, so findet man Richtung und Betrag zeichnerisch durch ein Kräfteparallelogramm. Die Kräfte $\vec{F_1}$ und $\vec{F_2}$ werden als Vektorpfeile dargestellt. Dann werden die Parallelen ergänzt. Die Diagonale des entstandenen Parallelogramms entspricht der Gesamtkraft. Allgemein kann die resultierende Kraft aus mehreren Kräften unterschiedlicher Richtung mit Hilfe der Vektorrechnung bestimmt werden, da die Kraft eine vektorielle Größe ist.

Weblinks

• Krafteinführung und Gesetz von Hooke
• Kraftaddition und Zerlegung
• Kräfte im Fach Physik für die Schule
• Flash-Animation zur Kräfteaddition (dwu-Unterrichtsmaterialien)
• Cornelis Harm Glimmerveen: The force of dialectics : on the logical and ontological structures concerning the concepts of force in Leibniz, Kant, and Hegel, Diss. Groningen 1992 (zum Kraftbegriff bei Leibniz, Kant und Hegel)
• Einheitenumrechnung für Kraft

Siehe auch

• Zugkraft, Druckkraft, Schließkraft
• Hand- und Armkraft