- Ungleichmäßig beschleunigte Kreisbewegung
-
Die reine Rotation, auch Rotationsbewegung, Drehung, Drehbewegung oder Kreisbewegung ist die Bewegung eines Punktes oder Körpers auf einer kreisförmigen Bahn (Weg).
Der Begriff der Rotation findet vor allem Verwendung in der Physik und hier im Speziellen in der Mechanik bzw. Kinematik. Anwendungen aus dem Alltag und oft zur anschaulichen Erklärung genutzte Beispiele, in der die Rotation eine wichtige Rolle spielt, sind der Kreisel, das Karussell, das Steinehüpfen sowie das Geschicklichkeitsspiel Astrojax.
Inhaltsverzeichnis
Eigenrotation und Rotationssystem
Die Rotation ist im Gegensatz zur reinen Translation keine Bewegung, die den Schwerpunkt des Körpers durch den Raum bewegt, sondern eine Bewegung des Körpers um eine Rotationsachse. Alle Punkte, die auf genau dieser Achse liegen, bleiben an der Stelle stehen, und alle anderen Punkte bewegen sich mit einer Geschwindigkeit, die proportional zur Entfernung von der Achse ist, auf einer idealen Kreisbahn. Hierbei kann sich die Achse im Körper selbst befinden, was zu einer Eigenrotation führt (Rotation um die eigene Achse), oder vom Körper entfernt liegen, was man als Rotationssystem bezeichnet (Rotation um eine gemeinsame Achse). Ursache für eine Rotation ist dabei jedoch immer die Wirkung eines Drehmomentes.
Kreisbahn, Rotationszentrum und Rotationsachse
Charakteristisch für eine Rotation ist, dass der Abstand zwischen einem ausgezeichneten Raumpunkt (Rotationszentrum) und einem bewegten Teilchen immer gleich groß ist, und die beschriebene Kreisbahn der jeweiligen Teilchen eine zweidimensionale Bewegungslinie ist. Für alle Punkte des Systems liegen diese ausgezeichneten Punkte auf einer Gerade, der Rotationsachse.
Hauptachsensystem und mitrotierendes System
Im allgemeinen stellt man den Ort des Punktes als Ortsvektor dar, setzt den Ursprung des Koordinatensystems in die Rotationsachse. Insbesondere dann, wenn das Koordinatensystem so gelegt wird, dass die z-Achse in Richtung des Drehimpulses zu liegen kommt, verschwindet sie in der Bewegungsgleichung, weil Letzterer normal auf die Bewegungsebene steht. Es handelt es sich um Hauptkoordinaten des Systems (ein Hauptachsensystem), und die Bewegungsgleichung enes Punktes in kartesischen Koordinaten lautet
So kann die Rotation als ebene Bewegung behandelt werden, und ein Teil der Bahnformel entspricht der Kreisgleichung. Hierbei ist auch R, der Abstand zum Zentrum, der Radius, konstant: Es gilt
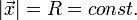
In zentralen Polarkoordinaten beschreibt man die Bahn sehr einfach als
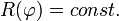 bzw.
bzw. 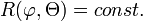 (kein Hauptachsensystem)
(kein Hauptachsensystem)
Der Radius ist unabhängig vom jeweiligen Zentriwinkel.
Noch einfacher beschreibt man die Bewegungsgleichung im mitrotierenden System, für die Bewegungsgleichung eines einzelnen Punktes ergibt sich
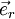 ist der (der Bewegung des Punktes folgende) Einheitsvektor in Richtung vom Ursprung zum Punkt, der mit seinem orthogonalen Einheitvektor das begleitende Zweibein des mitrotierenenden Koordinatensystems bildet.
ist der (der Bewegung des Punktes folgende) Einheitsvektor in Richtung vom Ursprung zum Punkt, der mit seinem orthogonalen Einheitvektor das begleitende Zweibein des mitrotierenenden Koordinatensystems bildet.Freiheitsgrade und Achsenbewegung
Jede Richtung, in welche eine Rotation erfolgen kann, ist gleichbedeutend mit einem zusätzlichen Rotationsfreiheitsgrad.
Eine Rotation mit nicht-konstanter Achse ist möglich und wird umgangssprachlich als „Torkeln“ oder „Eiern“ bezeichnet. Techniker und Wissenschaftler sprechen hingegen - je nach Art der Achsenbewegung - von Taumeln der Achse oder von sekundären Achsfehlern, bzw. von Präzession oder Nutation.
Vergleich mit der Translationsbewegung
Die folgende Tabelle vergleicht die charakteristischen Größen und die Bewegungsgleichungen bei einer Translationsbewegung mit jenen bei einer Rotationsbewegung. Aufgrund der Analogien lässt sich jeder Satz über die Translation durch Ersetzen der entsprechenden Größen in einen Satz über die Rotation umwandeln.[1]
Translationsbewegung Rotationsbewegung Weg : 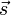
Drehwinkel : 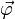 (5)
(5)Geschwindigkeit : 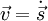 (1)
(1)Winkelgeschwindigkeit : 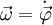 (1)(3)
(1)(3)Beschleunigung : 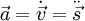
Winkelbeschleunigung : 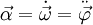 (4)
(4)Masse : m (Skalar) Trägheitstensor : Θ (Tensor zweiter Stufe)(2) Kraft : 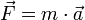
Drehmoment : 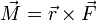
Impuls : 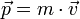
Drehimpuls : 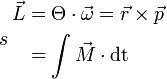
Kraftstoß / Antrieb : 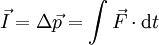
Kinetische Energie : 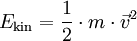
Rotationsenergie : 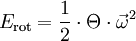
Arbeit : 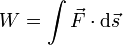
Arbeit bei Drehbewegung : 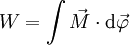
Leistung : 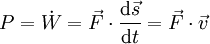
Leistung bei Drehbewegung : 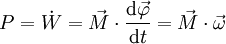
Bewegungsgleichungen Allgemein: Kraft ist mit Impulsänderung verknüpft (Impulssatz) : 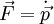
Allgemein: Drehmoment ist mit Drehimpulsänderung verknüpft (Drehimpulssatz) : 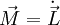
Im Falle konstanter Masse m (Zweites newtonsches Axiom) : 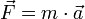
Im Falle konstanten Trägheitsmoments J :(2) 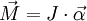
-
(2) Im Allgemeinen zeigen
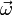 und
und 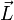 nicht in die gleiche Richtung – ein rotierender Körper „eiert“, – daher ist das Trägheitsmoment im Allgemeinen nicht konstant. Das Äquivalent zur Masse der Translationsbewegung ist daher ein Tensor 2. Stufe – der Trägheitstensor. Ein konstantes Trägheitsmoment tritt genau dann auf, wenn der Körper um eine seiner Hauptträgheitsachsen rotiert.
nicht in die gleiche Richtung – ein rotierender Körper „eiert“, – daher ist das Trägheitsmoment im Allgemeinen nicht konstant. Das Äquivalent zur Masse der Translationsbewegung ist daher ein Tensor 2. Stufe – der Trägheitstensor. Ein konstantes Trägheitsmoment tritt genau dann auf, wenn der Körper um eine seiner Hauptträgheitsachsen rotiert. -
(4) hier tritt zusätzlich eine Zentripetalbeschleunigung in Erscheinung, die bei der Translation nicht auftritt: Darum sind translative Systeme Inertialsysteme, rotative nicht.
Rotation fester Körper
Die Rotation fester Körper folgt den Eulerschen Gleichungen, zu denen es keine Lösung in Form einer einfachen Formel gibt. Selbst wenn keine äußeren Kräfte auf den Körper wirken, zeigt die Rotationsachse in den meisten Fällen eine komplexe Bewegung, die Nutation genannt wird. Es gibt jedoch für die technische Anwendung bedeutsame Spezialfälle, bei denen sich die Eulerschen Gleichungen soweit vereinfachen, dass sich einfache Lösungen ergeben. In diesen Fällen sind die Trajektorien des Systems periodisch.
Fall von Euler
Der Fall von Euler beschreibt einen Kreisel, der genau in seinem Schwerpunkt aufgehängt ist. Unabhängig von der Form des Kreisels ist der Fall integrabel, da es mehr Erhaltungsgrößen als Freiheitsgrade gibt: die Energie und die Drehimpulse bezüglich aller drei Hauptträgheitsachsen des Körpers.
Ist die Masse des rotierenden Körpers rings um die Drehungsachse symmetrisch verteilt, so wirken auf die Achse keinerlei aus der Rotation entspringende Kräfte, da ja die Schwungkraft (Zentrifugalkraft) eines jeden Massenteilchens durch eine gleiche und entgegen gesetzte aufgehoben wird; eine solche Achse wird eine freie Achse genannt. Da jedes um eine freie Achse rotierende Massenteilchen der Trägheit folgend in seiner zur Achse senkrechten Drehungsebene zu verharren strebt, muss auch die freie Achse selbst die Tendenz zeigen, ihre Richtung im Raum zu bewahren und so wird einer Kraft, welche sie aus dieser Richtung bringen will, einen umso größeren Widerstand entgegensetzen, je größer das Trägheitsmoment und die Winkelgeschwindigkeit des rotierenden Körpers sind. Daher kommt es, dass ein hinlänglich rasch rotierender Kreisel nicht umfällt, selbst wenn seine Achse schief steht, wie auch Räder, Münzen etc. nicht umfallen, wenn man sie auf ihrem Rand rollen oder um den vertikalen Durchmesser "tanzen" lässt.
Die Wirkung der störenden Kraft auf den Kreisel äußert sich vielmehr dadurch, dass dessen Achse in einer zur Richtung der störenden Kraft senkrechten Richtung ausweicht und in langsamer Bewegung die Oberfläche eines Kegels beschreibt, ohne dass die Achse ihre Neigung gegen die horizontale Ebene ändert. Diese Bewegung wird als Präzession bezeichnet.
Der Eulersche Kreisel findet z.B. in Kreiselkompassen und gyroskopischen Steuersystemen technische Anwendung. Auch die Räder von Fahrrädern und Motorrädern sind in guter Näherung Eulersche Kreisel und dienen neben der Spurführung des Fahrzeugs durch ihr Bestreben, den Drehimpuls zu erhalten, zur Stabilisierung des Fahrzeugs. Siehe hierzu auch: Fahrradfahren.
Fall von Lagrange
Für den Fall von Lagrange wird die Übereinstimmung der Trägheitsmomente bezüglich zweier Hauptachsen angenommen. Dies wird von radialsymmetrischen Körpern erfüllt. In diesem Fall gibt es mit drei Erhaltungsgrößen ebenso viele wie Freiheitsgrade: die Energie, den Gesamtdrehimpuls und den Drehimpuls bezüglich der z-Achse (in Richtung des Kraftfeldes). Dieser Fall wird durch einen typischen Spielzeugkreisel realisiert, wenn man dessen Aufsetzpunkt am Boden fixiert.
Fall von Kowalewskaja
Der Kowalewskaya-Kreisel hat bezüglich zweier seiner Hauptachsen gleiche Trägheitsmomente und ein genau doppelt so großes bezüglich der dritten Hauptachse. Die Erhaltungsgrößen sind die Energie, der Gesamtdrehimpuls und ein komplexer mathematischer Ausdruck, für den es keine allgemeinverständliche Entsprechung gibt.
Fall von Goryachew-Chaplygin
Der Fall von Goryachew-Chaplygin[2] ist eine Abwandlung des Kowalewskaja-Falles, der statt doppelt so großem dritten Trägheitsmoment ein viermal so großes fordert. In diesem Fall gibt es allerdings nur dann eine dritte Erhaltungsgröße, wenn der Drehimpuls um die z-Achse verschwindet.
Unabhängig von anderen Einflüssen ist jeder Kreisel quasi-integrabel, bei dem entweder sehr wenig oder sehr viel Energie (im Vergleich zur potentiellen Energiedifferenz zwischen unterem und oberem Totpunkt) in der Rotation steckt. Die chaotischsten Bewegungen bei den nicht integrablen Typen treten unabhängig von der Form dann auf, wenn die kinetische Energie des Kreisels gerade ausreicht, den oberen Totpunkt zu erreichen.
Siehe auch
- Rotation (Mathematik), Rotationsfläche
- Drehung, Drehrichtung, Drehzahl
- Gebundene Rotation, Differentielle Rotation, Erdrotation
- Kreisel, Rotationsperiode
- Rotationsmatrix, Quaternionen
- Direktionsmoment
- Gyrometer
- Harmonische Schwingung
- erste kosmische Geschwindigkeit
Einzelnachweise
- ↑ Hans Schmiedel, Johannes Süss: Physik - für technische Berufe. 16. Auflage, Büchner, Hamburg 1963, S. 74
- ↑ Theoretische Untersuchung des Fall von Goryachew-Chaplygin
Weblinks
Wikimedia Foundation.

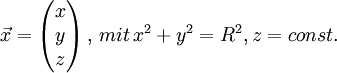
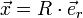
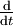 )
)