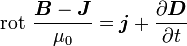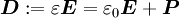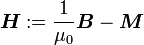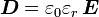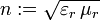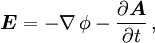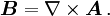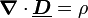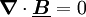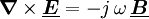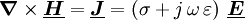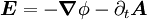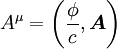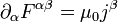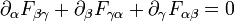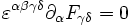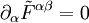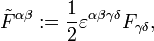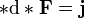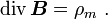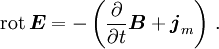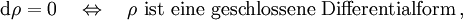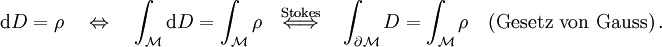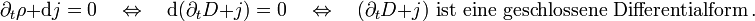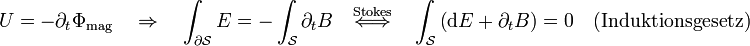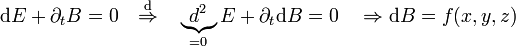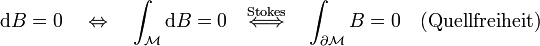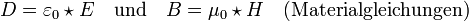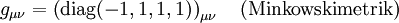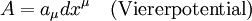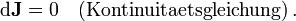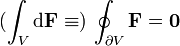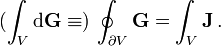- Maxwell’sche Gleichungen
-
Die vier maxwellschen Gleichungen beschreiben die Erzeugung von elektrischen und magnetischen Feldern durch Ladungen und Ströme, sowie die Wechselwirkung zwischen diesen beiden Feldern, die bei zeitabhängigen Feldern als Zeitentwicklung in Erscheinung tritt. Sie sind die Grundlage der Elektrodynamik und der theoretischen Elektrotechnik und wurden in den Jahren 1861 bis 1864 von James Clerk Maxwell entwickelt. Im Wesentlichen fasste Maxwell die bis zu diesem Zeitpunkt entdeckten Gesetzmäßigkeiten
- das ampèresche Gesetz,
- das Induktionsgesetz von Faraday und
- das gaußsche Gesetz
in einer vereinheitlichten Theorie zusammen und ergänzte sie um
- den maxwellschen Verschiebungsstrom,
um Konsistenz mit der Kontinuitätsgleichung zu erhalten. Die maxwellschen Gleichungen sind ein Beispiel für eine vereinheitlichte Theorie, die verschiedene Phänomene, hier magnetische und elektrische, in einer geschlossenen Form erklärt.
Übersicht
Für das Verständnis der folgenden Gleichungen sind Grundkenntnisse in Vektoranalysis erforderlich. Die maxwellschen Gleichungen lassen sich in differentieller und in integraler Form darstellen. Die Äquivalenz beider Formulierungen beruht auf dem Satz von Stokes und dem Satz von Gauß. Daneben gibt es eine elegante vierdimensionale Formulierung, die sogenannte kovariante Form (s. u.), die z. B. in der Relativitätstheorie und der Quantenelektrodynamik verwendet wird.
Hier werden die maxwellschen Gleichungen in SI-Einheiten angegeben. Formulierungen in anderen Einheitensystemen sind am Schluss aufgeführt bzw. werden durch Bemerkungen im Text erläutert.
Maxwellsche Gleichungen in SI-Einheiten differentielle Form verknüpfender Integralsatz Integralform Physikalisches gaußsches Gesetz: Das 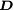 -Feld ist ein Quellenfeld. Die Ladung (Ladungsdichte ρ) ist Quelle des elektrischen Feldes.
-Feld ist ein Quellenfeld. Die Ladung (Ladungsdichte ρ) ist Quelle des elektrischen Feldes.Gauß Der (elektrische) Fluss durch die geschlossene Oberfläche  eines Volumens V ist gleich der elektrischen Ladung in seinem Inneren.
eines Volumens V ist gleich der elektrischen Ladung in seinem Inneren.
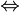

Das 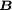 -Feld ist quellenfrei. Es gibt keine magnetischen Monopole.
-Feld ist quellenfrei. Es gibt keine magnetischen Monopole.Gauß Der magnetische Fluss durch die geschlossene Oberfläche eines Volumens ist gleich der magnetischen Ladung in seinem Inneren, nämlich Null, da es keine magnetischen Monopole gibt. 
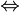

Induktionsgesetz (Vorsicht: Die Integralformulierung ist an dieser Stelle allgemeiner.):
Jede Änderung des
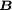 -Feldes führt zu einem elektrischen Gegenfeld. Die Wirbel des elektrischen Feldes sind von der zeitlichen Änderung der magnetischen Induktion abhängig.
-Feldes führt zu einem elektrischen Gegenfeld. Die Wirbel des elektrischen Feldes sind von der zeitlichen Änderung der magnetischen Induktion abhängig.Stokes Die (elektrische) Zirkulation über der Randkurve 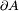 einer Fläche A ist gleich der negativen zeitlichen Änderung des magnetischen Flusses durch die Fläche.
einer Fläche A ist gleich der negativen zeitlichen Änderung des magnetischen Flusses durch die Fläche.
Hinweis: Die unten dargestellte Formel gilt, letztlich wegen der relativistischen Invarianz der Maxwell-Theorie, in der angegebenen Form auch bei zeitlich veränderlicher Fläche. Die Integralformulierung ist in diesem Punkt allgemeiner.
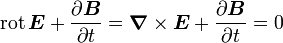
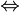
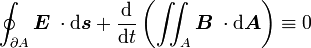
Verallgemeinertes Durchflutungsgesetz: (Hinweis: Bezüglich der größeren Allgemeinheit der Integralformulierung gilt analoges wie beim Induktionsgesetz.)
Die Wirbel des Magnetfeldes hängen von der elektrischen Leitungsstromdichte
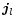 und von der elektrischen Flussdichte
und von der elektrischen Flussdichte 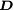 ab. Die zeitliche Änderung von
ab. Die zeitliche Änderung von 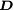 wird auch als Verschiebungsstromdichte
wird auch als Verschiebungsstromdichte 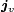 bezeichnet und ergibt als Summe mit der Leitungsstromdichte die totale Stromdichte
bezeichnet und ergibt als Summe mit der Leitungsstromdichte die totale Stromdichte  :
:Stokes (A ist eine Fläche mit Orientierung, 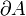 ihre Randkurve mit dem tangentialen Linienelement
ihre Randkurve mit dem tangentialen Linienelement 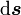 ;
; 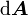 ist ein Flächenelement von A, multipliziert mit dem Vektor der äußeren Normalenrichtung.)
ist ein Flächenelement von A, multipliziert mit dem Vektor der äußeren Normalenrichtung.)
Die magnetische Zirkulation über der Randkurve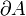 einer Fläche A ist gleich der Summe aus dem (elektrischen) Strom und der zeitlichen Änderung des elektrischen Flusses durch die Fläche.
einer Fläche A ist gleich der Summe aus dem (elektrischen) Strom und der zeitlichen Änderung des elektrischen Flusses durch die Fläche.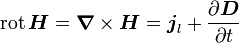
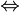
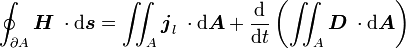
Erläuterungen
In den obigen Gleichungen sind Vektoren und Vektorfelder durch Fettdruck angedeutet.
Elektrischer Strom
In der elektrischen Stromdichte
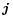 kann rein formal sowohl die übliche Leitungsstromdichte entsprechend dem Fluss von elektrischen Ladungsträgern als auch der Verschiebungsstrom (die zeitliche Änderung des elektrischen Feldes) zusammengefasst werden, was eine wichtige Rolle bei der Entdeckung der Maxwellgleichungen durch Maxwell spielte. Üblicherweise wird aber der Verschiebungsstrom getrennt aufgeführt. Die elektrische Stromdichte ist über die Materialgleichungen der Elektrodynamik und der dabei auftretenden elektrischen Leitfähigkeit σ mit der elektrischen Feldstärke
kann rein formal sowohl die übliche Leitungsstromdichte entsprechend dem Fluss von elektrischen Ladungsträgern als auch der Verschiebungsstrom (die zeitliche Änderung des elektrischen Feldes) zusammengefasst werden, was eine wichtige Rolle bei der Entdeckung der Maxwellgleichungen durch Maxwell spielte. Üblicherweise wird aber der Verschiebungsstrom getrennt aufgeführt. Die elektrische Stromdichte ist über die Materialgleichungen der Elektrodynamik und der dabei auftretenden elektrischen Leitfähigkeit σ mit der elektrischen Feldstärke 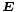 verknüpft.
verknüpft.Elektrisches Feld
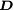 ist die elektrische Flussdichte, historisch und etwas verwirrend auch als elektrische Verschiebungsdichte oder als elektrische Erregung bezeichnet. Hierbei handelt es sich um die Dichte des elektrischen Flusses, welcher von elektrischen Ladungen ausgeht. Die elektrische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretenden dielektrischen Leitfähigkeit
ist die elektrische Flussdichte, historisch und etwas verwirrend auch als elektrische Verschiebungsdichte oder als elektrische Erregung bezeichnet. Hierbei handelt es sich um die Dichte des elektrischen Flusses, welcher von elektrischen Ladungen ausgeht. Die elektrische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretenden dielektrischen Leitfähigkeit 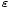 mit der elektrischen Feldstärke
mit der elektrischen Feldstärke 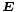 verknüpft. Noch allgemeiner gilt
verknüpft. Noch allgemeiner gilt 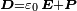 mit der elektrischen Polarisation
mit der elektrischen Polarisation 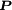 , dem elektrischen Dipolmoment pro Volumen.
, dem elektrischen Dipolmoment pro Volumen.Magnetisches Feld
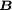 ist die magnetische Flussdichte, auch historisch als Induktion bezeichnet. Hierbei handelt es sich um die Dichte des magnetischen Flusses, welcher von bewegten elektrischen Ladungen oder von Permanentmagneten verursacht wird. Die magnetische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretende magnetische Leitfähigkeit μ mit der magnetischen Feldstärke
ist die magnetische Flussdichte, auch historisch als Induktion bezeichnet. Hierbei handelt es sich um die Dichte des magnetischen Flusses, welcher von bewegten elektrischen Ladungen oder von Permanentmagneten verursacht wird. Die magnetische Flussdichte ist über die Materialgleichungen der Elektrodynamik und die dabei auftretende magnetische Leitfähigkeit μ mit der magnetischen Feldstärke 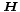 verknüpft. Noch allgemeiner gilt
verknüpft. Noch allgemeiner gilt 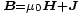 mit der magnetischen Polarisation
mit der magnetischen Polarisation 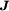 , dem magnetischen Dipolmoment pro Volumen (als Magnetisierung wird die im Weiteren zu
, dem magnetischen Dipolmoment pro Volumen (als Magnetisierung wird die im Weiteren zu 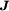 äquivalente Größe
äquivalente Größe 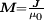 bezeichnet).
bezeichnet).Die magnetische Polarisation
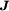 sollte nicht mit der Stromdichte
sollte nicht mit der Stromdichte 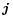 verwechselt werden. Vielmehr gilt:
verwechselt werden. Vielmehr gilt:Erläuterung zu den Maxwellgleichungen mit Materie
Die in allen drei Bereichen auftretenden Materialgleichungen werden nicht direkt zu den maxwellschen Gleichungen gezählt, sondern die drei Gleichungssätze:
- Maxwellsche Gleichungen
- Materialgleichungen der Elektrodynamik
- Kontinuitätsgleichungen der Elektrodynamik
stellen gemeinsam und unter gegenseitiger Ergänzung das Fundament der elektrodynamischen Feldtheorie dar. Die Materialgleichungen gelten in der allgemeinen Form sowohl für den leeren Raum als auch für mit Materie ausgefüllte Raumbereiche.
Aus historischen Gründen und manchmal auch um bestimmte Berechnungsvorgänge spezifisch darzustellen, werden die Materiegleichungen und die darin auftretenden drei Leitfähigkeiten jeweils in den Anteil des leeren Raumes
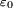 bzw.
bzw. 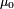 und den Anteil der Leitfähigkeit, welcher durch die Materie verursacht wird,
und den Anteil der Leitfähigkeit, welcher durch die Materie verursacht wird,  und
und 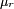 aufgespalten.
aufgespalten.Für das elektrische Feld ergibt sich durch die Aufspaltung der dielektrischen Leitfähigkeit die Möglichkeit zur Einführung eines weiteren Vektorfeldes, der elektrischen Polarisation
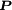 (eigentlich dielektrische Polarisation, die aber auch als elektrische Polarisation bezeichnet wird, da dem elektrischen Feld zugewiesen).
(eigentlich dielektrische Polarisation, die aber auch als elektrische Polarisation bezeichnet wird, da dem elektrischen Feld zugewiesen).Analog dazu beschreibt die magnetische Polarisation
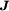 die von den Eigenschaften des leeren Raumes losgelösten Verhältnisse in Materie für das magnetische Feld. Aus der magnetischen Polarisation ergibt sich die Magnetisierung
die von den Eigenschaften des leeren Raumes losgelösten Verhältnisse in Materie für das magnetische Feld. Aus der magnetischen Polarisation ergibt sich die Magnetisierung 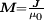 . (Im cgs-System sind die Verhältnisse verwirrender:
. (Im cgs-System sind die Verhältnisse verwirrender: 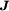 und
und 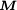 werden dort gleich bezeichnet, als cgs-Magnetisierung, und unterscheiden sich nur um einen Faktor
werden dort gleich bezeichnet, als cgs-Magnetisierung, und unterscheiden sich nur um einen Faktor 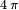 , je nachdem ob
, je nachdem ob 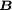 oder
oder 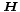 gemeint ist.)
gemeint ist.)Grundsätzlich kann ohne Verlust auf die Einführung der Vektorfelder der elektrischen Polarisation
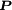 und der magnetischen Polarisation
und der magnetischen Polarisation 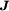 (bzw. der dazu äquivalenten Magnetisierung
(bzw. der dazu äquivalenten Magnetisierung 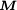 ) verzichtet werden. Statt dessen werden die Abhängigkeiten in den Materialgleichungen und den entsprechend allgemein gefassten Leitfähigkeiten in Form von Tensoren höherer Ordnung berücksichtigt. Weiterhin können die Leitfähigkeiten auch Funktionen darstellen, um nichtlineare Eigenschaften der Materie erfassen zu können. Diese können sogar von der Vorbehandlung abhängen, also explizit zeitabhängig sein. Diese Vorgangsweise empfiehlt sich auch für einen systematischen Zugang, wenn dieser über das SI-Einheitensystem erfolgt. Aus historischen Gründen, aber auch in bestimmten Teilbereichen der Physik, wird allerdings manchmal sehr intensiv von den
) verzichtet werden. Statt dessen werden die Abhängigkeiten in den Materialgleichungen und den entsprechend allgemein gefassten Leitfähigkeiten in Form von Tensoren höherer Ordnung berücksichtigt. Weiterhin können die Leitfähigkeiten auch Funktionen darstellen, um nichtlineare Eigenschaften der Materie erfassen zu können. Diese können sogar von der Vorbehandlung abhängen, also explizit zeitabhängig sein. Diese Vorgangsweise empfiehlt sich auch für einen systematischen Zugang, wenn dieser über das SI-Einheitensystem erfolgt. Aus historischen Gründen, aber auch in bestimmten Teilbereichen der Physik, wird allerdings manchmal sehr intensiv von den 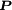 - und
- und 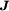 - (bzw.
- (bzw. 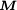 -) Vektorfeldern Gebrauch gemacht, weshalb im Folgenden dieser Sachverhalt näher dargestellt wird.
-) Vektorfeldern Gebrauch gemacht, weshalb im Folgenden dieser Sachverhalt näher dargestellt wird.In Materie gilt allgemein
sowie
bzw.
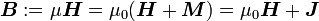 ,
,
wobei sich im Spezialfall der Linearität bei Isotropie oder bei kubischen Systemen noch folgende Vereinfachung ergibt:
und
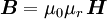 .
.
In homogenen isotropen Materialien (d. h.
 und μ sind skalar und konstant) erhält man für die Maxwellgleichungen
und μ sind skalar und konstant) erhält man für die Maxwellgleichungen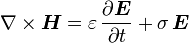
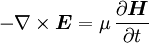
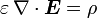
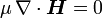 .
.
In anisotroper nicht-kubischer linearer Materie werden die Skalare
 und
und 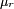 zu Tensoren 2. Stufe, wobei die Beziehungen weiterhin Gültigkeit behalten. In nichtlinearen Materialien hängen die Leitfähigkeiten von den jeweiligen Momentanwerten der Feldstärken oder im allgemeinsten Fall von deren gesamter Geschichte ab (siehe Hysterese). Die
zu Tensoren 2. Stufe, wobei die Beziehungen weiterhin Gültigkeit behalten. In nichtlinearen Materialien hängen die Leitfähigkeiten von den jeweiligen Momentanwerten der Feldstärken oder im allgemeinsten Fall von deren gesamter Geschichte ab (siehe Hysterese). Die 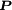 - und
- und 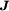 -Felder, elektrische bzw. magnetische Polarisation genannt, verschwinden außerhalb der Materie, was in den genannten Spezialfällen gleichwertig mit der Aussage ist, dass
-Felder, elektrische bzw. magnetische Polarisation genannt, verschwinden außerhalb der Materie, was in den genannten Spezialfällen gleichwertig mit der Aussage ist, dass 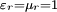 wird.
wird.Die dielektrische Polarisation ist dann mit der elektrischen Suszeptibilität
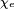 , bzw. der relativen Permittivität
, bzw. der relativen Permittivität  und der Vakuum-Permittivität (Dielektrizitätskonstante)
und der Vakuum-Permittivität (Dielektrizitätskonstante) 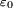 folgendermaßen verknüpft (im SI-System, d. h. in der Einheit
folgendermaßen verknüpft (im SI-System, d. h. in der Einheit 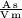 ):
):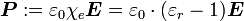 ,
,
mit
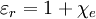 .
.
Für die magnetische Polarisation
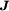 bzw. die Magnetisierung
bzw. die Magnetisierung 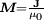 gilt eine entsprechende Gleichung mit der magnetischen Suszeptibilität
gilt eine entsprechende Gleichung mit der magnetischen Suszeptibilität 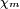 bzw. der relativen Permeabilität
bzw. der relativen Permeabilität 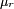 und der Vakuum-Permeabilität (magnetische Feldkonstante)
und der Vakuum-Permeabilität (magnetische Feldkonstante) 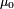 mit der Einheit
mit der Einheit 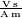 :
: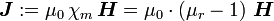 ,
,
mit
- μr = 1 + χm.
(Vorsicht: im cgs-System sind
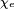 und
und 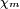 mit
mit 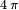 zu multiplizieren!)
zu multiplizieren!)Weiter ergibt sich die Definition der Brechzahl mit
und der Lichtgeschwindigkeit im Vakuum
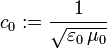 ,
,
was die Lichtgeschwindigkeit im Material mit den entsprechenden Konstanten in Verbindung bringt. So ist die Phasengeschwindigkeit im Medium
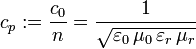 ,
,
die bei frequenzunabhängiger Brechzahl (ohne Dispersion) gleich der Gruppengeschwindigkeit im Medium ist.
Zusammenfassung
Maxwellgleichungen in SI-Einheiten Ampèresches Gesetz 
Faradaysches Gesetz 
Coulombsches Gesetz 
Gaußsches Gesetz des Magnetismus 


Traditionell werden die beiden zuletzt angegebenen sog. Materialgesetze und das Ohm'sche Gesetz
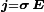 (σ ist hierbei der spezifische elektrische Leitwert) meist nicht in die Maxwellgleichungen miteinbezogen. Auch die Kontinuitätsgleichung
(σ ist hierbei der spezifische elektrische Leitwert) meist nicht in die Maxwellgleichungen miteinbezogen. Auch die Kontinuitätsgleichung 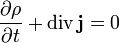 , welche die Ladungserhaltung definiert, wird meist nicht erwähnt.
, welche die Ladungserhaltung definiert, wird meist nicht erwähnt.Die elektrischen Feldstärken E sowie die magnetischen Flussdichten B werden als physikalisch vorhandene Kraftfelder interpretiert. Schon Maxwell verband diese Kraftfelder mit dem elektrischen Potenzialfeld
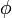 und dem Vektorpotenzial
und dem Vektorpotenzial 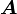 :
:Der Zusammenhang zwischen Feldstärken und Potenzialen ist zwar nur bis auf Eichtransformationen definiert, den Potentialen kommt aber in der Quantentheorie eine fundamentale Bedeutung zu.[2].
Maxwellgleichungen für konstante Frequenzen ω in komplexer Schreibweise
Die in den maxwellschen Gleichungen auftretenden Feldvektoren sind im allgemeinen nicht nur Funktionen des Ortes sondern auch der Zeit, beispielsweise
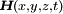 . In den partiellen Differentialgleichungen tritt dann neben den Ortsvariablen auch die Zeitvariable auf. Zur vereinfachten Lösung dieser Differentialgleichungen beschränkt man sich in der Praxis oft auf harmonische (sinusförmige) Vorgänge. Diese Darstellung ist für die praktische Feldberechnung, beispielsweise bei der Berechnung von elektromagnetischen Schirmen oder für die Antennentechnik, von wesentlicher Bedeutung.
. In den partiellen Differentialgleichungen tritt dann neben den Ortsvariablen auch die Zeitvariable auf. Zur vereinfachten Lösung dieser Differentialgleichungen beschränkt man sich in der Praxis oft auf harmonische (sinusförmige) Vorgänge. Diese Darstellung ist für die praktische Feldberechnung, beispielsweise bei der Berechnung von elektromagnetischen Schirmen oder für die Antennentechnik, von wesentlicher Bedeutung.Mit Hilfe der komplexen Schreibweise lässt sich die Zeitabhängigkeit bei harmonischen Vorgängen vermeiden, da sich der komplexe Zeitfaktor
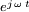 dabei heraushebt. Die in den maxwellschen Gleichungen auftretenden Feldgrößen sind dann komplexe Amplituden und nur noch Funktionen des Ortes. An Stelle der partiellen Differentiation nach der Zeit tritt die Multiplikation mit dem imaginären Faktor
dabei heraushebt. Die in den maxwellschen Gleichungen auftretenden Feldgrößen sind dann komplexe Amplituden und nur noch Funktionen des Ortes. An Stelle der partiellen Differentiation nach der Zeit tritt die Multiplikation mit dem imaginären Faktor 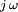 . Der Faktor ω wird auch als Kreisfrequenz bezeichnet.
. Der Faktor ω wird auch als Kreisfrequenz bezeichnet.Hierbei wird wie in der Elektrotechnik üblich die imaginäre Einheit mit j bezeichnet (sie sollte nicht mit der häufig für die Stromdichte verwendeten Variable j verwechselt werden) - in Mathematik und theoretischer Physik wird sie meist i geschrieben.
In komplexer Form, komplexe Größen sind zur Unterscheidung unterstrichen, lauten die maxwellschen Gleichungen in Differentialform:
Kovariante Formulierung der Maxwellgleichungen
- In diesem Absatz wird, wie im übrigen Artikel, das SI-Einheitensystem verwendet. Dieses und die damit verbundenen Faktoren
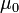 ,
, 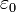 etc. empfinden viele Theoretiker gerade bei der kovarianten Formulierung der Elektrodynamik als unnatürlich und verwenden andere Systeme, etwa Gauß-Einheiten oder Heaviside-Lorentz-Einheiten, in denen die Grundgrößen der Elektrodynamik anders definiert werden. In der Literatur können deshalb verglichen mit dieser Darstellung Vorfaktoren wegfallen, hinzukommen oder an andere Stellen rücken.
etc. empfinden viele Theoretiker gerade bei der kovarianten Formulierung der Elektrodynamik als unnatürlich und verwenden andere Systeme, etwa Gauß-Einheiten oder Heaviside-Lorentz-Einheiten, in denen die Grundgrößen der Elektrodynamik anders definiert werden. In der Literatur können deshalb verglichen mit dieser Darstellung Vorfaktoren wegfallen, hinzukommen oder an andere Stellen rücken.
Die Elektrodynamik, wie sie durch die Maxwellgleichungen beschrieben wird, ist im Gegensatz zur newtonschen Mechanik verträglich mit der speziellen Relativitätstheorie. Dazu gehört, dass die Maxwellgleichungen in jedem Inertialsystem gelten, ohne dass sich beim Wechsel des Bezugssystems ihre Form ändert. Dies spielte historisch für die Entwicklung der Relativitätstheorie durch Albert Einstein eine wichtige Rolle.[3].
Technischer formuliert sind die Maxwellgleichungen relativistisch kovariant oder forminvariant, das heißt, dass sie ihre Gestalt unter Lorentz-Transformationen nicht ändern.
Diese Eigenschaft ist den Maxwellgleichungen in der oben beschriebenen Form jedoch nicht ohne weiteres anzusehen. Es kann deshalb nützlich sein, durch eine Umformulierung der Theorie die Forminvarianz herauszuarbeiten, anders ausgedrückt: die Theorie „manifest kovariant“ zu schreiben.
Hierzu ist es zweckmäßig, die oben auftretenden Größen
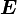 ,
, 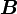 usw. durch Größen ausdrücken, die ein klar definiertes, einfaches Transformationsverhalten unter Lorentz-Transformationen haben, also durch Lorentz-Skalare, Vierervektoren und Vierer-Tensoren höherer Stufen.
usw. durch Größen ausdrücken, die ein klar definiertes, einfaches Transformationsverhalten unter Lorentz-Transformationen haben, also durch Lorentz-Skalare, Vierervektoren und Vierer-Tensoren höherer Stufen.
Ausgangspunkt für diese Umformulierung bilden die elektromagnetischen Potentiale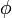 (skalares Potential) und
(skalares Potential) und 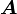 (Vektorpotential), aus denen man die elektrischen und magnetischen Felder durch
(Vektorpotential), aus denen man die elektrischen und magnetischen Felder durcherhält (siehe auch Elektrodynamik). Diese Größen lassen sich zu einem Vierervektor, dem Viererpotential
zusammenfassen. Ebenso kann man aus Ladungsdichte
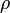 und Stromdichte
und Stromdichte 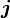 die Viererstromdichte zusammensetzen, mit
die Viererstromdichte zusammensetzen, mit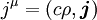 .
.
Aus dem Viererpotential wird der elektrodynamische Feldstärketensor abgeleitet, dessen Komponenten bis auf Vorzeichen und konstante Vorfaktoren, die vom Einheitensystem abhängen, gerade die der elektrischen und magnetischen Felder sind. Er hat die Form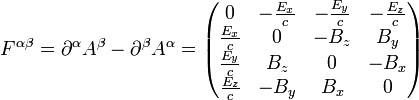 .
.
Man definiert nun den Vierergradienten, die relativistische Form der Ableitung, als
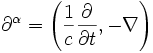 , also
, also 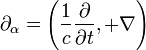 , sowie die Differentiale
, sowie die Differentiale 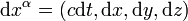 , die bei der Behandlung der maxwellschen Gleichungen im Artikel Differentialformen benötigt werden, der an dieser Stelle auch empfohlen wird.
, die bei der Behandlung der maxwellschen Gleichungen im Artikel Differentialformen benötigt werden, der an dieser Stelle auch empfohlen wird.
Mit diesen Größen kann man die beiden inhomogenen Maxwellgleichungen im Vakuum durch die kovariante Gleichung
ersetzen. Dabei wird, wie üblich, die einsteinsche Summenkonvention benutzt, das heißt, über doppelt auftretende Indizes in Produkten (hier α) wird summiert. Ferner erfolgt wie üblich das Herauf- und Herunterziehen von Indizes mit dem metrischen Tensor
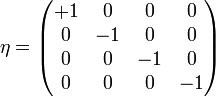 .
.
Man beachte, dass wegen der Antisymmetrie des Feldstärketensors auch die Kontinuitätsgleichung (Verschwinden der Vierer-Divergenz) folgt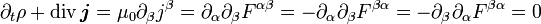 .
.
Die beiden homogenen Maxwellgleichungen erhalten im Vakuum die manifest kovariante FormDies wird auch häufig mit dem Levi-Civita-Symbol kompakter geschrieben als
oder
mit dem dualen Feldstärketensor
dessen Komponenten man auch aus denen von
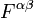 erhalten kann, indem man die Vektoren
erhalten kann, indem man die Vektoren 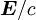 durch
durch 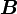 und
und 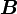 durch
durch 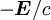 ersetzt. Also
ersetzt. Also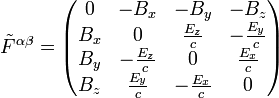 .
.
Differentialformen ermöglichen eine besonders übersichtliche Darstellung der Maxwellgleichungen, die zudem automatisch kovariant ist, wenn man von Anfang an nicht im euklidischen Raum, sondern im Minkowski-Raum arbeitet. Dabei werden Viererpotential und Viererstromdichte durch die 1-Formen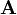 und
und 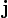 dargestellt, der Feldstärketensor durch die 2-Form
dargestellt, der Feldstärketensor durch die 2-Form 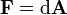 und sein Dual durch die 2-Form
und sein Dual durch die 2-Form 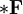 (das Symbol d steht bei Differentialformen für eine formale Ableitung und nicht etwa für ein unendlich kleines Differential). Die Maxwellgleichungen im Vakuum lauten dann (in Heaviside-Lorentz-Einheiten)
(das Symbol d steht bei Differentialformen für eine formale Ableitung und nicht etwa für ein unendlich kleines Differential). Die Maxwellgleichungen im Vakuum lauten dann (in Heaviside-Lorentz-Einheiten) und
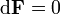 .
.
Maxwellgleichungen unter Berücksichtigung hypothetischer magnetischer Monopole
Magnetische Monopole treten in einigen GUT-Theorien als mögliche oder notwendige Bestandteile auf. Mit ihnen ließe sich die Quantelung der elektrischen Ladung erklären, wie Paul Dirac schon 1931 erkannte. Bislang ist allerdings kein magnetischer Monopol beobachtet worden. Daher wird in den oben genannten Maxwellgleichungen auch angenommen, dass keine magnetischen Monopole (magnetische Ladungen) existieren.
Sollten in der Zukunft dennoch solche magnetischen Ladungen gefunden werden, so lassen sich diese in den Maxwellgleichungen problemlos berücksichtigen.
Setzt man ρm für die Monopolladungsdichte,
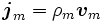 für die Stromdichte und
für die Stromdichte und 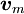 für die Geschwindigkeit der sich bewegenden magnetischen Monopolladungen, so ändern sich nur zwei der vier oben genannten Gleichungen in differentieller Form zu
für die Geschwindigkeit der sich bewegenden magnetischen Monopolladungen, so ändern sich nur zwei der vier oben genannten Gleichungen in differentieller Form zuInterpretation: Die Feldlinien der magnetischen Flussdichte beginnen und enden in einer magnetischen Ladung.
Interpretation: Sich zeitlich ändernde magnetische Flussdichten oder das Vorhandensein von magnetischen Stromdichten führen zu elektrischen Wirbelfeldern.
Die anderen beiden Gleichungen bleiben unverändert, während sich aber natürlich für die beiden neuen differentiellen (d. h. lokalen) Gleichungen auch neue integrale (d. h. globalen) Darstellungen ergeben, die aber ohne weiteres mit den Integralsätzen von Gauß und Stokes berechnet werden können.
Der Fall der verschwindenden Monopole ρm = 0 führt wieder auf die bekannten, oben angegebenen Gleichungen zurück.
Maxwellsche Gleichungen und Photonmasse
Die Photonmasse verschwindet gemäß der maxwellschen Gleichungen. Diese Gleichungen sind der Grenzfall m = 0 der allgemeineren Maxwell-Proca-Gleichungen mit einer nicht negativen Photonmasse m. Statt des Coulomb-Potentials
 bewirkt in der Maxwell-Proca-Theorie eine elektrische Punktladung q das Yukawa-Potential
bewirkt in der Maxwell-Proca-Theorie eine elektrische Punktladung q das Yukawa-Potential 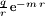 und hat nur noch eine Reichweite von etwa der Compton-Wellenlänge, die zu m gehört.
und hat nur noch eine Reichweite von etwa der Compton-Wellenlänge, die zu m gehört.Maxwellsche Gleichungen in differentialgeometrischer Form
Die Beschreibung durch die Vektoranalysis hat den großen Nachteil, dass sie
- auf den flachen
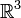 bzw.
bzw.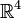 beschränkt ist
beschränkt ist - prinzipiell "metrisch verseucht" ist, da entweder die euklidische oder die Lorentz'sche Metrik in den Operatoren verbaut ist, obwohl die Maxwellgleichungen metrikfrei definiert sind
- die Wahl einer Karte der zugrundeliegenden Mannigfaltigkeit völlig unphysikalisch ist, da Naturgesetze unabhängig von den gewählten Koordinaten richtig sein müssen
Der 3-dimensionale Ansatz
Didaktisch ist es sinnvoll, die Invarianz der Maxwellgleichungen unter Lorentztransformationen erst einmal zu verbergen und mit einer 3-dimensionalen Mannigfaltigkeit zu starten. Die Zeit wird als äußerer Parameter behandelt, wie aus der klassischen Mechanik gewohnt.
Die inhomogenen Maxwellgleichungen
Sei
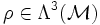 eine Differentialform auf der beliebigen glatten Mannigfaltigkeit
eine Differentialform auf der beliebigen glatten Mannigfaltigkeit 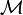 der Dimension 3 und d die äußere Ableitung. Dann ist
der Dimension 3 und d die äußere Ableitung. Dann istweil es keine von 0 verschiedene Differentialform vom Grad 4 auf einer 3-dimensionalen Mannigfaltigkeit geben kann. Auf einem sternförmigen Gebiet sichert das Lemma von Poincaré, dass ein Potential
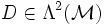 existiert, sodass
existiert, sodassDieses "Gesetz von Gauß" darf nicht mit dem Gauß'schen Integralsatz verwechselt werden, zumal letzterer nur ein Spezialfall des allgemeinen Satzes von Stokes ist. -
Weiterhin wird postuliert, dass die zeitliche Ableitung der Ladung
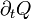 aus einer Mannigfaltigkeit einem Strom durch die Berandung entgegengesetzt ist (sprich: alles was aus dem "Volumen"
aus einer Mannigfaltigkeit einem Strom durch die Berandung entgegengesetzt ist (sprich: alles was aus dem "Volumen" 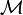 heraus will, muss durch die Berandungsfläche
heraus will, muss durch die Berandungsfläche 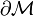 fließen).
fließen).Diese Aussage entspricht also dem zur Kontinuitätsgleichung gehörigen Erhaltungssatz für die Gesamtladung (die Beliebigkeit der Mannigfaltigkeit
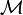 sichert analog zum Gesetz von Gauß, dass dieser auch ohne Integrale gilt).
sichert analog zum Gesetz von Gauß, dass dieser auch ohne Integrale gilt). 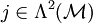 wird Stromdichte(zweiform) genannt. Also:
wird Stromdichte(zweiform) genannt. Also:Diese mathematische Aussage impliziert aber nach dem Lemma von Poincaré, dass auf einem sternförmigen Gebiet eine Differentialform vom Grad 1
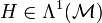 existiert, sodass
existiert, sodassAnzumerken ist, dass das Gesetz von Gauß rein aus der Geometrie des Problems folgt, also letztlich keine physikalische Bedeutung hat: Der einzige physikalische Input ist die Existenz elektrischer Ladungen bzw. die Kontinuitätsgleichung, welche im Maxwell-Ampere-Gesetz mündet. Die inhomogenen Gleichungen sind also Folge der Ladungserhaltung. Nichtbetroffen ist im Grunde nur der sog. Spinmagnetismus, d. h. derjenigen magnetischen Phänomene, die nicht von den hier ausschließlich behandelten Ampèreschen Kreisströmen (den Wirbeln von j ) herrühren (siehe Mathematische Struktur der Quantenmechanik, speziell den Abschnitt über den Spin, sowie den Artikel über das sog. Gyromagnetische Verhältnis). Dies betrifft den dominierenden Teil des sog. Permanent-Magnetismus. Das zeigt aber im Grunde nur, dass die klassische Elektrodynamik nicht in sich selbst abgeschlossen ist, obwohl es mathematisch und theoretisch-physikalisch so scheint.
Die homogenen Maxwellgleichungen
Ähnlich der Kontinuitätsgleichung wird das Induktionsgesetz postuliert. Die zeitliche Änderung des magnetischen Flusses durch eine Fläche
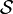 geht einher mit der Induktion einer entgegengesetzten Ringspannung auf ihrem Rand
geht einher mit der Induktion einer entgegengesetzten Ringspannung auf ihrem Rand 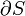 . Das ist völlig analog zur Kontinuitätsgleichung, nur eine Dimension tiefer.
. Das ist völlig analog zur Kontinuitätsgleichung, nur eine Dimension tiefer.Dabei ist
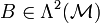 die magnetische Flussdichte(zweiform) und
die magnetische Flussdichte(zweiform) und 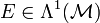 das elektrische Feld. Die Beliebigkeit der Fläche
das elektrische Feld. Die Beliebigkeit der Fläche 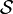 sichert, dass sich das Induktionsgesetz auch ohne Integral schreiben lässt:
sichert, dass sich das Induktionsgesetz auch ohne Integral schreiben lässt:Man erkennt also, dass dB nur von den (Raum)-Komponenten der Mannigfaltigkeit
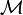 abhängen kann, nicht aber von der Zeit. Jedoch hängt der Ausdruck links vom Gleichheitszeichen gar nicht von der Wahl der Koordinaten ab. Also muss f(x,y,z) verschwinden. Zusätzlich kann die Gleichung auch nur dann lorentzinvariant sein. Es folgt also die Quellfreiheit der magnetischen Flussdichte(zweiform) (d.h. die Nichtexistenz magnetischer Ladungen, siehe oben):
abhängen kann, nicht aber von der Zeit. Jedoch hängt der Ausdruck links vom Gleichheitszeichen gar nicht von der Wahl der Koordinaten ab. Also muss f(x,y,z) verschwinden. Zusätzlich kann die Gleichung auch nur dann lorentzinvariant sein. Es folgt also die Quellfreiheit der magnetischen Flussdichte(zweiform) (d.h. die Nichtexistenz magnetischer Ladungen, siehe oben):Wieder geht lediglich ein Postulat ein, das Induktionsgesetz; die Quellfreiheit ist dann eine rein mathematische Konsequenz.
Relativistische Invarianz
Die relativistische Invarianz ergibt sich aus einem subtilen Punkt, den man u.U. leicht übersieht: Oben sind wir bei einem Integral der Form
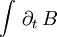 gelandet, d.h. es sieht so aus, als ob nur dann „etwas passiert“ (d.h. eine Induktionsspannung auftritt), wenn sich das Magnetfeld selbst ändert. In Wirklichkeit besagt Faradays Induktionsgesetz, dass eine Induktionsspannung immer dann auftritt, wenn sich das Magnetfeld relativ zur Spule ändert. D.h., das Differential nach der Zeit kann nicht hinter dem Integral verbleiben, sondern muss vor das Integral gezogen werden, so dass auch bei bloßer Änderung der Spule, bei festgehaltenem Magnetfeld, eine Induktionsspannung auftritt.
gelandet, d.h. es sieht so aus, als ob nur dann „etwas passiert“ (d.h. eine Induktionsspannung auftritt), wenn sich das Magnetfeld selbst ändert. In Wirklichkeit besagt Faradays Induktionsgesetz, dass eine Induktionsspannung immer dann auftritt, wenn sich das Magnetfeld relativ zur Spule ändert. D.h., das Differential nach der Zeit kann nicht hinter dem Integral verbleiben, sondern muss vor das Integral gezogen werden, so dass auch bei bloßer Änderung der Spule, bei festgehaltenem Magnetfeld, eine Induktionsspannung auftritt.Die Materialgleichungen
Weil die Einsformen E und H nicht kompatibel mit den Zweiformen D und B sind, muss man eine Beziehung zwischen ihnen herstellen. Das geschieht mit dem Hodgeoperator
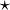 , welcher auf einer 3-dimensionalen Mannigfaltigkeit Einsformen und Zweiformen durch den Isomorphismus der Dualität verbindet (siehe oben).
, welcher auf einer 3-dimensionalen Mannigfaltigkeit Einsformen und Zweiformen durch den Isomorphismus der Dualität verbindet (siehe oben).Hier wird offensichtlich, warum H und B bzw. E und D schon aus mathematischen Gründen nicht einfach (bis auf einen Faktor) identifiziert werden können. H ist ja eine Einsform und wird über eine Kurve integriert, B ist eine Zweiform und braucht eine (2-dimensionale) Fläche zur Integration. (Zudem sind in polarisierbaren Medien die zugehörigen Vektorfelder auch physikalisch wesentlich verschieden.) Es kann also schon von der Mathematik her keine Proportionalität zwischen diesen Größen bestehen, wie es die Beschreibung durch die Vektoranalysis suggeriert. Gleiches gilt für E und D: Die erste Größe beschreibt eine Differentialform vom Grade 1, braucht zur Integration also eine Kurve, wie bei einem Kraft-Integral; die zweite Größe ist eine Zweiform, braucht also eine Fläche wie bei einem Fluss-Integral. Dieser Unterschied scheint pedantisch, ist aber fundamental.
Es sei bemerkt, dass erst mit dem Hodgeoperator die Metrik eine Rolle in den Gleichungen spielt. Die Maxwellgleichungen ohne die Materialgleichungen sind unabhängig von der Wahl der Metrik und sogar unabhängig von der Beschaffenheit der Mannigfaltigkeit, solange
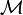 dreidimensional ist. Lediglich die Wirkung von
dreidimensional ist. Lediglich die Wirkung von 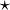 in den Materialgleichungen würde sich verändern.
in den Materialgleichungen würde sich verändern.Der 4-dimensionale Ansatz
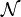 sei eine glatte Mannigfaltigkeit der Dimension 4 und
sei eine glatte Mannigfaltigkeit der Dimension 4 und 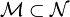 eine glatte Untermannigfaltigkeit der Dimension 3 (aus dem 3-dimensionalen Ansatz) und
eine glatte Untermannigfaltigkeit der Dimension 3 (aus dem 3-dimensionalen Ansatz) und 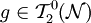 der metrische Tensor mit Koeffizientendarstellung.
der metrische Tensor mit Koeffizientendarstellung.(Es gibt viele äquivalente Formen, die man z.B. durch Multiplikation mit einer Zahl vom Betrag 1 erhalten kann.) )
Die Metrik muss lediglich festgelegt werden, damit man das nun folgende Viererpotential
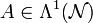 explizit hinschreiben kann (Physik: „kontravariante Größen“), ohne den Umweg über die Koeffizienten eines Vektorfeldes (Physik: „kovariante Größen“)
explizit hinschreiben kann (Physik: „kontravariante Größen“), ohne den Umweg über die Koeffizienten eines Vektorfeldes (Physik: „kovariante Größen“) 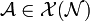 zu gehen mit
zu gehen mit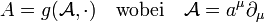 .
.
Die Festlegung auf den Minkowskiraum, die man u.a. benötigt um „raumartige“ und „zeitartige“ Vektor- bzw. Tensorkomponenten zu unterscheiden, oder bei der Definition der Dualitätsoperation (siehe unten), ist also hier nicht erforderlich Man könnte die Metrik auch frei wählen, dann sähen die Komponenten der Einsform
nur anders aus, denn
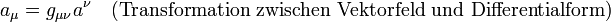 .
.
Sei also ab hier die Mannigfaltigkeit der flache Minkowskiraum, das heißt o.B.d.A.
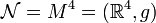 . Dann ist das Vektorpotential gegeben durch
. Dann ist das Vektorpotential gegeben durch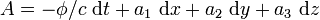 für das Vektorfeld
für das Vektorfeld 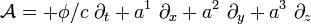 .
.
Die homogenen Maxwellgleichungen
Sei nun die äußere Ableitung von A gegeben durch
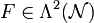 , also durch den sog. Feldstärketensor (Faradayzweiform):
, also durch den sog. Feldstärketensor (Faradayzweiform):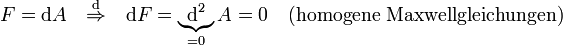 .
.
Beeindruckend ist die Tatsache, dass die äußere Ableitung von F immer verschwindet, unabhängig davon, wie A aussieht. Das ergibt die sog. Eichfreiheit und begründet auch, warum die Einschränkung auf den Minkowskiraum die Allgemeinheit nicht verletzt. Da die Gleichungen jedoch ohne jeden physikalischen Input auskommen, folgt unmittelbar, dass die homogenen Maxwellgleichungen lediglich Folge der Geometrie des Raumes und des benutzten Formalismus sind (gleiches gilt ja auch für die Beziehung
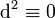 : eine geschlossene Differentialform ist ja noch weitgehend frei, nämlich bis auf das äußere Differential einer um ein Grad niedrigeren Form. ).
: eine geschlossene Differentialform ist ja noch weitgehend frei, nämlich bis auf das äußere Differential einer um ein Grad niedrigeren Form. ).Die Materialgleichungen
Die Faradayzweiform lässt sich auch in den bereits bekannten Größen schreiben:
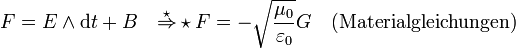 .
.
Die zu F duale[4] Zweiform G heißt Maxwellzweiform und ist gegeben durch schon bekannten Größen, nämlich:
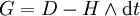 .
.
In physikalischen Theorien entspricht F dem Feldstärketensor und G dessen dualem Tensor (siehe unten).
Die gesamten Maxwellgleichungen, mit nur zwei Differentialformen
Definiert man nun eine Dreiform
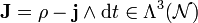 , so ergibt deren äußere Ableitung
, so ergibt deren äußere AbleitungDies entspricht dem schon erwähnten Erhaltungssatz für die Gesamtladung.
Während nun die beiden homogenen Maxwell-Gleichungen (Maxwell I und II) durch die Aussage zusammengefasst werden können, dass die elektrischen bzw. magnetischen Felder
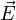 bzw.
bzw. 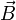 durch eine einzige geschlossene Differentialform zweiter Stufe
durch eine einzige geschlossene Differentialform zweiter Stufe 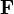 repräsentiert werden (
repräsentiert werden (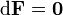 ), gilt für die verbleibenden inhomogenen Maxwell-Gleichungen III und IV die Aussage, dass die äußere Ableitung der dualen Form
), gilt für die verbleibenden inhomogenen Maxwell-Gleichungen III und IV die Aussage, dass die äußere Ableitung der dualen Form 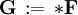 mit der Stromform
mit der Stromform 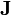 identisch ist. Also
identisch ist. Also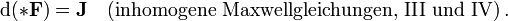 .
.
Damit ist die Gesamtheit aller vier Maxwell-Gleichungen in mathematischer Kurzform durch nur zwei Differentialformen,
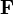 und
und 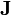 , ausgedrückt. (Insbesondere folgt aus der letzten Gleichung sofort auch die Kontuitätsgleichung, weil die zweimalige äußere Ableitung immer Null ergibt.)
, ausgedrückt. (Insbesondere folgt aus der letzten Gleichung sofort auch die Kontuitätsgleichung, weil die zweimalige äußere Ableitung immer Null ergibt.)Erneut spielt die Metrik keine direkte Rolle (indirekt ist sie sehr wichtig, z. B. bei der Definition der Dualität, die bei der Berechnung der Ladungen und Ströme aus den Feldern benötigt wird) sowie bei der Angabe der expliziten Form der Lorentzinvarianz. Auch die Mannigfaltigkeit
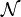 ist beliebig, solange sie Dimension 4 hat. Letztlich ist aber physikalisch auch hier die Metrik wesentlich, nicht nur bei der gerade erwähnten Dualität. Sondern auch hier kommt es nicht allein auf die Vierdimensionalität der Mannigfaltigkeit an, sondern auch auf die Unterscheidung zwischen Raum- und Zeitkoordinaten (bzw. zwischen sog. raumartigen und sog. zeitartigen Vektoren, Tensor- und Feldkomponenten), die sich ja mit Hilfe des metrischen Tensors ausdrücken. Dieser ist ja nicht gegeben durch
ist beliebig, solange sie Dimension 4 hat. Letztlich ist aber physikalisch auch hier die Metrik wesentlich, nicht nur bei der gerade erwähnten Dualität. Sondern auch hier kommt es nicht allein auf die Vierdimensionalität der Mannigfaltigkeit an, sondern auch auf die Unterscheidung zwischen Raum- und Zeitkoordinaten (bzw. zwischen sog. raumartigen und sog. zeitartigen Vektoren, Tensor- und Feldkomponenten), die sich ja mit Hilfe des metrischen Tensors ausdrücken. Dieser ist ja nicht gegeben durch 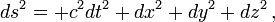 sondern z. B. durch
sondern z. B. durch 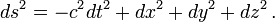 D.h. man hat es nicht mit einer
D.h. man hat es nicht mit einer 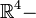 , sondern, wie schon gesagt, mit einer
, sondern, wie schon gesagt, mit einer 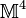 -Mannigfaltigkeit zu tun. Die Unterscheidung von „raumartigen“ und „zeitartigen“ Größen in der Metrik hängt auch mit dem Unterschied zwischen elektrischen und magnetischen Feldern zusammen. Obwohl die (insgesamt sechs) Feldkomponenten dieser Größen durch die Lorentz-Beziehungen ineinander transformiert werden können, ist die Charakterisierung eines Feldes als im Wesentlichen „elektrisch“ bzw. „magnetisch“ eine Invariante der Theorie, weil die Lagrange-Funktion, eine aus *F, F und J zusammengesetzte invariante Funktion, aus der sich die Bewegungsgleichungen (also die Maxwellschen Gleichungen) berechnen lassen, im cgs-System im Wesentlichen gleich B2-E2 ist. (Bemerkung: Ein Minkowski-Vektor
-Mannigfaltigkeit zu tun. Die Unterscheidung von „raumartigen“ und „zeitartigen“ Größen in der Metrik hängt auch mit dem Unterschied zwischen elektrischen und magnetischen Feldern zusammen. Obwohl die (insgesamt sechs) Feldkomponenten dieser Größen durch die Lorentz-Beziehungen ineinander transformiert werden können, ist die Charakterisierung eines Feldes als im Wesentlichen „elektrisch“ bzw. „magnetisch“ eine Invariante der Theorie, weil die Lagrange-Funktion, eine aus *F, F und J zusammengesetzte invariante Funktion, aus der sich die Bewegungsgleichungen (also die Maxwellschen Gleichungen) berechnen lassen, im cgs-System im Wesentlichen gleich B2-E2 ist. (Bemerkung: Ein Minkowski-Vektor 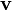 ist raumartig bzw. zeitartig bzw. lichtartig, je nachdem ob
ist raumartig bzw. zeitartig bzw. lichtartig, je nachdem ob ![(ds)^2[\mathbf v]](/pictures/dewiki/49/13f502f1b9890f8e43eb2e71a253918c.png) positiv bzw. negativ bzw. Null ist. Analog ist ein elektromagnetisches Feld im Wesentlichen magnetisch bzw. elektrisch bzw. wellenartig je nachdem ob die Lagrangefunktion, für
positiv bzw. negativ bzw. Null ist. Analog ist ein elektromagnetisches Feld im Wesentlichen magnetisch bzw. elektrisch bzw. wellenartig je nachdem ob die Lagrangefunktion, für 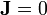 , positiv bzw. negativ bzw. Null ist.)
, positiv bzw. negativ bzw. Null ist.)Abstrakte Integralformulierung und Interpretation
Diese abstrakte differentielle Formulierung der Maxwellschen Gleichungen benutzt die Theorie der sog. alternierenden Differentialformen, insbesondere das sog. äußere Differential. Die zugehörige abstrakte Integralformulierung ergibt sich durch Anwendung des verallgemeinerten Stokesschen Satzes aus dieser mathematischen Theorie: Man konzentriert sich dazu in der angegebenen Drei-Mannigfaltigkeit V mit Minkowski-Metrik (z. B. eingebettet in den Raum
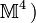 besonders auf deren Rand
besonders auf deren Rand 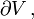 eine geschlossene Zwei-Mannigfaltigkeit, und erhält:
eine geschlossene Zwei-Mannigfaltigkeit, und erhält:für alle V, sowie (mit
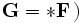 :
:Dabei steht der eigentlich interessierende Teil hinter der Klammer und es wird durch das Zeichen
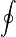 im Sinne der Physik betont, dass das Integrationsgebiet
im Sinne der Physik betont, dass das Integrationsgebiet 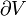 eine geschlossene Mannigfaltigkeit ist. Die erste der beiden angegebenen Gleichungen enthält das Faradaysche Induktionsgesetz und das Gesetz von der Nichtexistenz magnetischer Ladungen. In der letzten Gleichung ist das Maxwell-Ampèresche Gesetz und das Gesetz von Gauß enthalten. Beide Gesetze eines Paares gehören also jeweils zusammen. Das Gaußsche Gesetz z.B. besagt in der hier gegebenen abstrakten Formulierung: Der Fluss der elektromagnetischen Form
eine geschlossene Mannigfaltigkeit ist. Die erste der beiden angegebenen Gleichungen enthält das Faradaysche Induktionsgesetz und das Gesetz von der Nichtexistenz magnetischer Ladungen. In der letzten Gleichung ist das Maxwell-Ampèresche Gesetz und das Gesetz von Gauß enthalten. Beide Gesetze eines Paares gehören also jeweils zusammen. Das Gaußsche Gesetz z.B. besagt in der hier gegebenen abstrakten Formulierung: Der Fluss der elektromagnetischen Form 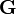 durch den Rand der Mannigfaltigkeit V ist gleich der gesamten in V enthaltenen „Ladung“, wie sie sich aus der Stromform
durch den Rand der Mannigfaltigkeit V ist gleich der gesamten in V enthaltenen „Ladung“, wie sie sich aus der Stromform 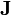 ergibt.
ergibt.Die angegebene Eichfreiheit ergibt sich geometrisch daraus, dass man zu vorgegebenem Rand
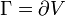 viele verschiedene Mannigfaltigkeiten V finden kann, die darin „hineinpassen“.
viele verschiedene Mannigfaltigkeiten V finden kann, die darin „hineinpassen“.Historische Bemerkungen
Maxwell veröffentlichte seine Gleichungen 1865[1]. Im Jahr 1873 brachte Maxwell seine Gleichungen in eine quaternionische Darstellung[5]. Im Zuge dessen hat Maxwell auch das magnetische Potenzialfeld
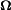 und die magnetische Masse m in seine Gleichungen eingeführt und diese Feldvariablen in die Gleichung für die elektromagnetische Kraft F eingefügt. Maxwell rechnete allerdings nicht direkt in dieser Notation, sondern behandelte den Skalarteil und den Vektorteil getrennt.
und die magnetische Masse m in seine Gleichungen eingeführt und diese Feldvariablen in die Gleichung für die elektromagnetische Kraft F eingefügt. Maxwell rechnete allerdings nicht direkt in dieser Notation, sondern behandelte den Skalarteil und den Vektorteil getrennt.Die heute gängigen Notationen wurden erst später von Oliver Heaviside[6] und Josiah Willard Gibbs[7] auf der Grundlage der ursprünglichen Maxwellschen Gleichungen von 1865 formuliert. Diese Notation ist einfacher zu lesen und in den meisten Fällen auch einfacher anzuwenden, weshalb diese Notationen auch heute noch üblich sind. Hierbei handelt es sich jedoch um eine Untermenge der ursprünglichen Gleichungen.
Maxwellgleichungen im cgs-System
Im gaußschen cgs-System lauten die Maxwellgleichungen[8]:
Maxwellgleichungen im gaußschen cgs-System Ampèresches Gesetz 
Induktionsgesetz 
Coulombsches Gesetz 
Gaußsches Gesetz des Magnetismus 
Manchmal wird eine Form des gaußschen cgs Systems verwendet, in dem der Strom in esu gemessen wird; dann muß j mit einem Faktor
 in den hier angegebenen Maxwellgleichungen versehen werden.
in den hier angegebenen Maxwellgleichungen versehen werden.Für die Potenziale wird im cgs-System gesetzt:
Bei der Formulierung der Maxwellgleichungen im cgs-System von Heaviside-Lorentz entfallen die Faktoren 4π in obigen Gleichungen. Bei der Formulierung in natürlichen Einheiten muß in den obigen Gleichungen c=1 gesetzt und die Faktoren 4π müssen weggelassen werden.
Literatur
- Wolfgang Panofsky, Melba Phillips: Classical Electricity and Magnetism, Addison Wesley (zuerst 1955)
- John David Jackson: Classical Electrodynamics, John Wiley (zuerst 1962)
- Károly Simonyi: Theoretische Elektrotechnik, Harri Deutsch
- Lew Landau, Jewgeni Lifschitz: Theoretische Physik Bd. 2: Klassische Feldtheorie, Harri Deutsch
- Richard Becker, Fritz Sauter: Theorie der Elektrizität, Bd. 1 (Einführung in die Maxwellsche Theorie, Elektronentheorie, Relativitätstheorie), Teubner
- Richard Feynman: Lectures on Physics, Bd. 2, Addison-Wesley
- Günther Lehner: Elektromagnetische Feldtheorie für Ingenieure und Physiker. 5. Auflage. Springer-Verlag, 2006, ISBN 978-3-5402-6550-4.
- Uwe Krey, Anthony Owen: Basic Theoretical Physics: A Concise Overview. Springer, Berlin, Berlin 2007, ISBN 978-3-5403-6804-5.
Referenzen
- ↑ a b James Clerk Maxwell, A Dynamical Theory of the Electromagnetic Field, Royal Society Transactions 155, 1865, Seiten 459–512
- ↑ Yakir Aharonov, David Bohm; „Significance of Electromagnetic Potentials in the Quantum Theory, Physical Review 115/3, 1959
- ↑ Albert Einstein, Zur Elektrodynamik bewegter Körper, Annalen der Physik und Chemie 17, 30. Juni 1905, Seiten 891-921
- ↑ Die Dualitätsoperation vertauscht u.a. kovariante und kontravariante Vektor-Komponenten. D.h.: hier ist der metrische Tensor wichtig.
- ↑ James Clerk Maxwell, A Treatise on Electricity & Magnetism, Dover Publications, New York 1873, ISBN 0-486-60636-8 und ISBN 0-486-60637-6
- ↑ Oliver Heaviside, On the Forces, Stresses and Fluxes of Energy in the Electromagnetic Field, Philosophical Transactions of the Royal Society 183A, 1892, Seite 423
- ↑ E. B. Wilson, Vector Analysis of Josiah Willard Gibbs – The History of a Great Mind, Charles Scribner’s Sons New York, 1901
- ↑ z.B. Panofsky, Phillips, 2. Auflage 1978, S.466. Dort sind im Anhang auch Erläuterungen zu den Maßeinheiten.
Weblinks
Wikimedia Foundation.