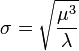Wald-Verteilung

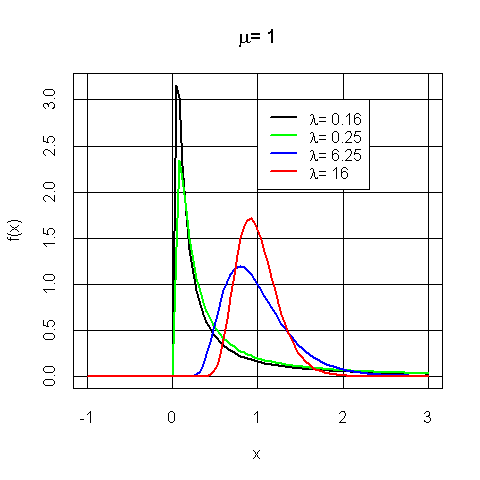
Die inverse Normalverteilung (auch inverse Gauß-Verteilung oder Wald-Verteilung genannt) ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Sie wird in verallgemeinerten linearen Modellen verwendet. Bei der Untersuchung der Brownschen Molekularewegung mit Drift v > 0 und Streuungskoeffizient λ > 0 ist die zufällige Zeit des ersten Erreichens des Niveaus a > 0 invers normalverteilt mit den Parametern $\left(\frac{a}{v},\frac{a^{2}}{\lambda^{2}}\right)$.

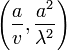siehe auch: Lévy-Prozess

Definition

Eine stetige Zufallsvariable X genügt der inversen Normalverteilung mit den Parametern λ > 0 (Ereignisrate) und μ > 0 (Mittelwert), wenn sie die Wahrscheinlichkeitsdichte 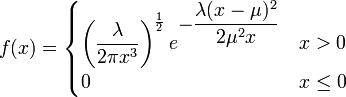$f(x)=\begin{cases}\displaystyle \left(\frac{\lambda}{2\pi x^3}\right)^{\frac{1}{2}}e^{\displaystyle -\frac{\lambda(x-\mu)^2}{2\mu^2x}} & x > 0 \\ 0 & x\leq 0 \end{cases}$ besitzt.

Eigenschaften

Erwartungswert

Die inverse Normalverteilung besitzt den Erwartungswert

$\operatorname{E}(X) = \mu$.

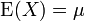Varianz

Die Varianz ergibt sich analog zu

$\operatorname{Var}(X) = \frac{\mu^3}{\lambda}$.

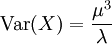Standardabweichung

Daraus erhält man für die Standardabweichung

$\sigma = \sqrt{\frac{\mu^3}{\lambda}}$

Variationskoeffizient

Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten

$\operatorname{VarK}(X) = \sqrt{\frac{\mu}{\lambda}}$.

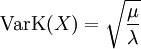Schiefe

Die Schiefe ergibt sich zu

$\operatorname{v}(X) = 3\sqrt{\frac{\mu}{\lambda}}$.

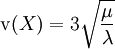Wölbung (Kurtosis)

Die Wölbung ergibt sich zu

$\beta_2 = \frac{15 \mu}{\lambda}$.

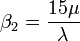Charakteristische Funktion

Die charakteristische Funktion hat die Form

$\phi_{X}(s) = e^{\frac{\lambda}{\mu}\left(1-\sqrt{1-\frac{2\mu^2is}{\lambda}}\right)}$.

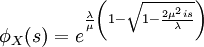Momenterzeugende Funktion

Die momenterzeugende Funktion der inversen Normalverteilung ist

$m_{X}(s) = e^{\frac{\lambda}{\mu}\left(1-\sqrt{1-\frac{2\mu^2s}{\lambda}}\right)}$.

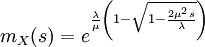Reproduzierbarkeit

Sind 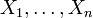$X_1, \dots, X_n$ Zufallsvariable mit inverser Normalverteilung mit den Parametern λ und μ, dann ist die Größe 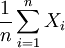$\frac{1}{n}\sum\limits_{i=1}^{n}X_{i}$ wieder eine Zufallsvariable mit einer inversen Normalverteilung, aber mit den Parametern nλ und μ.

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart