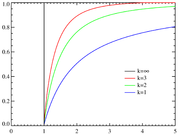
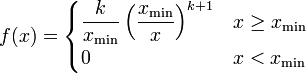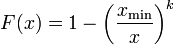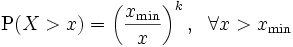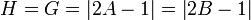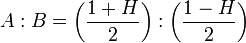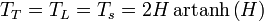Pareto-Regel

Die Pareto-Verteilung, benannt nach dem italienischen Ingenieur, Soziologen und Ökonomen Vilfredo Pareto (1848–1923), ist eine stetige Wahrscheinlichkeitsverteilung.

Definition

Pareto-Wahrscheinlichkeitsdichte f(x) mit (x_min=1).

Kumulative Verteilungsfunktion F(x)

Eine stetige Zufallsvariable X heißt pareto-verteilt 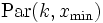$\operatorname{Par}(k,x_{\min})$ mit den Parametern k > 0 und x_min > 0, wenn sie die Wahrscheinlichkeitsdichte

$f(x)= \begin{cases}\displaystyle \frac{k}{x_{\min}}\left(\frac{x_{\min}}{x}\right)^{k+1} & x\geq x_{\min} \\ 0 & x<x_{\min} \end{cases}$

besitzt.

Die Wahrscheinlichkeit, mit der die Zufallsvariable X einen Wert kleiner oder gleich x annimmt, errechnet sich damit mit der Verteilungsfunktion:

$F(x)= 1-\left(\frac{x_{\min}}{x}\right)^{k}$

Dabei ist k ein sogenannter Fitparameter, d.h. er wird an vorliegende Werte (z.B. Stichproben) angepasst. Der Parameter k beschreibt das Größenverhältnis der Zufallswerte in Abhängigkeit von ihrer Häufigkeit.

Damit errechnet sich die Wahrscheinlichkeit, dass die Zufallsvariable X Werte größer x annimmt durch:

${\rm P}(X>x)=\left(\frac{x_{\min}}{x}\right)^{k},~~\forall x > x_{\min}$

Eigenschaften

Erwartungswert

Der Erwartungswert ergibt sich zu:

$\operatorname{E}(X) = \begin{cases}\displaystyle x_{\min} \frac{k}{k-1} & k > 1\\ \infty & k \leq 1 \end{cases}$.

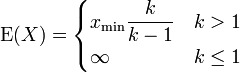Varianz

Die Varianz ergibt sich zu

$\operatorname{Var} (X) = \begin{cases}\displaystyle x_{\min}^2 \left( \frac{k}{k-2} - \frac{k^2}{(k-1)^2} \right) = x_{\min}^2 \frac{k}{(k-2)(k-1)^2} & k > 2 \\ \infty & k \leq 2 \end{cases}$.

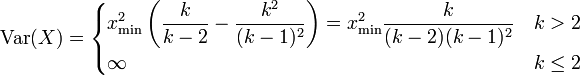Weitere Momente ergeben sich entsprechend.

Standardabweichung

Aus der Varianz ergibt sich für k > 2 die Standardabweichung

$\sigma(X) = \frac{x_{\min}}{k-1} \sqrt{\frac{k}{k-2}}$.

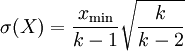Variationskoeffizient

Aus Erwartungswert und Standardabweichung erhält man für k > 2 sofort den Variationskoeffizienten

$\operatorname{VarK}(X) = \frac{1}{\sqrt{k(k-2)}}$.

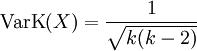Schiefe

Für die Schiefe erhält man für k > 3

$\operatorname{v}(X) = \frac{\displaystyle\frac{k}{k-3}-3\frac{k^2}{(k-2)(k-1)}+2\frac{k^3}{(k-1)^3}} {\displaystyle\left(\frac{k}{k-2}-\frac{k^2}{(k-1)^2}\right)^{\frac{3}{2}}} =\frac{2(1+k)}{k-3}\,\sqrt{\frac {k-2}2}$.

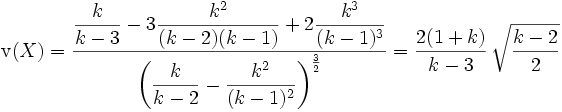Charakteristische Funktion

Die charakteristische Funktion ergibt sich zu: $k(-ix_\mathrm{min}t)^k\Gamma(-k,-ix_\mathrm{min}t)\,$.

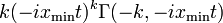Momenterzeugende Funktion

Die momenterzeugende Funktion ist für die Pareto-Verteilung nicht in geschlossener Form angebbar.

Entropie

Die Entropie ergibt sich zu: $\log\left(\frac{k}{x_\mathrm{min}}\right) - \frac{1}{k} - 1\!$.

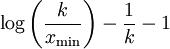Zipfsches Gesetz

Das Zipfsche Gesetz ist mathematisch mit der Pareto-Verteilung identisch (x- und y-Achse sind vertauscht). Während die Pareto-Verteilung die Wahrscheinlichkeit bestimmter Zufallswerte betrachtet, fokussiert das Zipfsche Gesetz die Wahrscheinlichkeit, mit der Zufallswerte eine bestimmte Position in der Rangfolge der Häufigkeit einnehmen.

Beziehung zur anderen Verteilungen

Beziehung zur Exponentialverteilung

Wenn X eine Pareto-verteilte Zufallsvariable 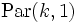$\operatorname{Par}(k,1)$ mit den Parametern k und 1 ist, dann ist logX exponentialverteilt 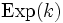$\operatorname{Exp}(k)$ mit dem Parameter k.

Beziehung zur verschobenen Pareto-Verteilung

Wenn X eine Pareto-verteilte Zufallsvariable ist, dann genügt 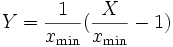$Y=\frac{1}{x_{\min}}(\frac{X}{x_{\min}}-1)$ einer verschobenen Pareto-Verteilung.

Ungleichverteilungsmaße und das Pareto-Prinzip

Für die Berechnung von Ungleichverteilungsmaßen beschreiben Verteilungen der Form „A zu B“ (A:B) zwei Quantile, wobei die Breite des ersten Quantils der Höhe des zweiten Quantils und die Höhe des ersten Quantils der Breite des zweiten Quantils gleicht. In der Lorenz-Kurve stellt sich dieser Sachverhalt in der Gestalt eines „stehenden“ und eines „liegenden“ Quantils dar. A und B müssen dabei jeweils im Bereich von 0 bis 1 liegen und es gilt: A + B = 1. Der Gini-Koeffizient und die Hoover-Ungleichverteilung sind in diesem Fall gleich:

$H=G=\left|2A-1 \right|=\left|2B-1 \right|$

$A:B = \left( \frac{1+H}{2} \right): \left( \frac{1-H}{2} \right)$

Für diese Zwei-Quantile-Verteilungen ist dann auch der Theil-Index (ein Entropie-Maß) einfach zu berechnen:

$T_T=T_L=T_s = 2 H \, \operatorname{artanh} \left( H \right)\,$

Das Paretoprinzip kann als Merkhilfe für den Wertebereich des Theil-Index dienen. Der Index hat bei einer Gleichverteilung von 0,5:0,5 (50 % zu 50 %) einen Wert von 0 und nimmt bei etwa 0,82:0,18 (82 % zu 18 %) den Wert 1 an^[1]. Das liegt ganz in der Nähe der Verteilung von 80% zu 20%. Oberhalb der Verteilung von 82% zu 18% ist der Theil-Index größer als 1.

Übersicht einiger markanter Verteilungen:

• 50 % zu 50 %: Gleichverteilung.
• 62 % zu 38 %: Der Theil-Index abzüglich der Hoover-Ungleichverteilung erreicht ein Minimum. Der Hoover-Ungleichverteilung liegt das Verteilungsmodell einer Umverteilung mit minimalem Aufwand zugrunde. Vollständige Steuerung minimiert hier die zum Erreichen einer Gleichverteilung erforderlichen Ressourcenbewegungen. Dem Theil-Index liegt das Verteilungsmodell eines rein stochastischen Umverteilungsprozesses zugrunde. Damit ist der Wert, der sich aus dem Theil-Index abzüglich der Hoover-Ungleichverteilung ergibt, der Wert der Information, die gegenüber einer rein stochastischen Umverteilung für eine Umverteilung mit minimalem Aufwand erforderlich ist. Zwischen Verteilungen von 50 % zu 50 % (Gleichverteilung) und 73% zu 27% ist dieser Wert negativ.
• 73 % zu 27 %: Der Theil-Index und die Hoover-Ungleichverteilung sind gleich.
• 74 % zu 26 %: Der Theil-Index liegt bei 0,5.
• 80 % zu 20 %: „Pareto-Prinzip“.
• 82 % zu 18 %: Der Theil-Index liegt bei 1. Im stochastischen Umverteilungsprozess werden bei dieser Ungleichverteilung alle Ressourcen bewegt. Bei höheren Ungleichverteilung werden mehr Ressourcen bewegt, als vorhanden. Das bedeutet, dass bei höheren Ungleichverteilungen Ressourcen auf dem Weg zum Equilibrium mehrfach umverteilt werden.
• 92 % zu 8 %: Der Theil-Index liegt bei 2. Im Mittel wird im stochastischen Umverteilungsprozess jede Ressource zweimal bewegt.
• 98 % zu 1 %: Der Theil-Index liegt bei 4.

Beispiele

Verteilung der Einwohnerzahl großer deutscher Städte

Doppeltlogarithmische Darstellung der Verteilung

Verteilungsdichte

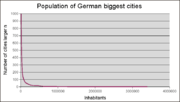
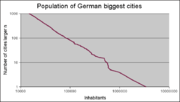
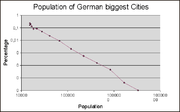
In Bezug auf die Größenverteilung von Städten zeigt die Grafik rechts die Anzahl deutscher Großstädte, die größer sind als die vom Parameter x vorgegebene Bevölkerungszahl. Die doppeltlogarithmische Auftragung lässt erkennen, dass die Verteilung einem Potenzgesetz folgt.

Der Exponent k der kumulativen Darstellung beträgt 1,31. Folglich lautet der Exponent der Dichtefunktion a= k+1 = 2,31, in guter Übereinstimmung mit der Literatur. Das Summieren der Werte bei der kumulativen Darstellung reduziert die Streuung der Messwerte. Um die Dichtefunktion zeichnen zu können, werden die Werte in Intervalle unterteilt und gezählt. Je nach Intervallgröße schwanken die Mittelwerte der Intervalle, oder die Kurve wegen der geringen Anzahl der Intervalle.

In diesem Artikel oder Abschnitt fehlen folgende wichtige Informationen: Erläuterung des Zusammenhangs zwischen Beispielen für Potenzverteilung und Pareto-Verteilung fehlt. Du kannst Wikipedia helfen, indem du sie recherchierst und einfügst.

Aus den Verteilungsfunktionen lässt sich das Paretoprinzip ablesen: 20% der Eingangsgrößen erfassen 80% der Gesamtmenge.

Weblinks

• Universität Konstanz - Interaktive Animation
• Einfaches Excel Werkzeug für eine Pareto Auswertung

Einzelnachweise

1. ↑ On-Line-Rechner: Ungleichverteilung

Diskrete univariate Verteilungen

Diskrete univariate Verteilungen für endliche Mengen:
Benford | Bernoulli-Verteilung | Binomialverteilung | Kategoriale | Hypergeometrische Verteilung | Rademacher | Zipfsche | Zipf-Mandelbrot

Diskrete univariate Verteilungen für unendliche Mengen:
Boltzmann | Conway-Maxwell-Poisson | Negative Binomialverteilung | Erweiterte negative Binomial | Compound Poisson | Diskret uniform | Discrete phase-type | Gauss-Kuzmin | Geometrische | Logarithmische | Parabolisch-fraktale | Poisson | Skellam | Yule-Simon | Zeta

 

Kontinuierliche univariate Verteilungen

Kontinuierliche univariate Verteilungen mit kompaktem Intervall:
Beta | Kumaraswamy | Raised Cosine | Dreiecks | U-quadratisch | Stetige Gleichverteilung | Wigner-Halbkreis

Kontinuierliche univariate Verteilungen mit halboffenem Intervall:
Beta prime | Bose-Einstein | Burr | Chi-Quadrat | Coxian | Erlang | Exponential | F | Fermi-Dirac | Folded Normal | Fréchet | Gamma | Extremwert | Verallgemeinerte inverse Gausssche | Halblogistische | Halbnormale | Hotellings T-Quadrat | hyper-exponentiale | hypoexponential | Inverse Chi-Quadrat | Scale Inverse Chi-Quadrat | Inverse Normal | Inverse Gamma | Lévy | Log-normal | Log-logistische | Maxwell-Boltzmann | Maxwell speed | Nakagami | nichtzentrierte Chi-Quadrat | Pareto | Phase-type | Rayleigh | relativistische Breit-Wigner | Rice | Rosin-Rammler | Shifted Gompertz | Truncated Normal | Type-2-Gumbel | Weibull | Wilks’ lambda

Kontinuierliche univariate Verteilungen mit unbeschränktem Intervall:
Cauchy | Extremwert | Exponential Power | Fisher’s z | Fisher-Tippett (Gumbel) | Generalized Hyperbolic | Hyperbolic Secant | Landau | Laplace | Alpha stabile | logistisch | Normal (Gauss) | Normal-inverse Gausssche | Skew normal | Studentsche t | Type-1 Gumbel | Variance-Gamma | Voigt

 

Multivariate Verteilungen

Diskrete multivariate Verteilungen:
Ewen's | Multinomial | Dirichlet Multinomial

Kontinuierliche multivariate Verteilungen:
Dirichlet | Generalized Dirichlet | Multivariate Normal | Multivariate Student | Normalskalierte inverse Gamma | Normal-Gamma

Multivariate Matrixverteilungen:
Inverse-Wishart | Matrix Normal | Wishart